right angle trigonometry problem solving

Right Triangle Trigonometry Calculator

Basics of trigonometry, right triangles trigonometry calculations, example of right triangle trigonometry calculations with steps, more trigonometry and right triangles calculators (and not only).

The right triangle trigonometry calculator can help you with problems where angles and triangles meet: keep reading to find out:

• The basics of trigonometry;
• How to calculate a right triangle with trigonometry;
• A worked example of how to use trigonometry to calculate a right triangle with steps;

And much more!

Trigonometry is a branch of mathematics that relates angles to the length of specific segments . We identify multiple trigonometric functions: sine, cosine, and tangent, for example. They all take an angle as their argument, returning the measure of a length associated with the angle itself. Using a trigonometric circle , we can identify some of the trigonometric functions and their relationship with angles.

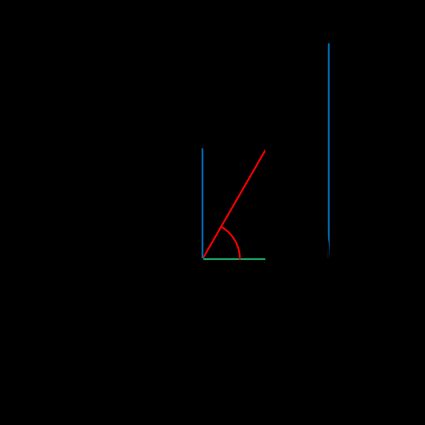
As you can see from the picture, sine and cosine equal the projection of the radius on the axis, while the tangent lies outside the circle. If you look closely, you can identify a right triangle using the elements we introduced above: let's discover the relationship between trigonometric functions and this shape.

Consider an acute angle in the trigonometric circle above: notice how you can build a right triangle where:

• The radius is the hypotenuse; and
• The sine and cosine are the catheti of the triangle.

α \alpha α is one of the acute angles, while the right angle lies at the intersection of the catheti (sine and cosine)

Let this sink in for a moment: the length of the cathetus opposite from the angle α \alpha α is its sine , sin ⁡ ( α ) \sin(\alpha) sin ( α ) ! You just found an easy and quick way to calculate the angles and sides of a right triangle using trigonometry.

The complete relationships between angles and sides of a right triangle need to contain a scaling factor, usually the radius (the hypotenuse). Identify the opposite and adjacent . We can then write:

By switching the roles of the legs, you can find the values of the trigonometric functions for the other angle.

Taking the inverse of the trigonometric functions , you can find the values of the acute angles in any right triangle.

Using the three equations above and a combination of sides, angles, or other quantities, you can solve any right triangle . The cases we implemented in our calculator are:

• Solving the triangle knowing two sides ;
• Solving the triangle knowing one angle and one side ; and
• Solving the triangle knowing the area and one side .

Take a right triangle with hypotenuse c = 5 c = 5 c = 5 and an angle α = 38 ° \alpha=38\degree α = 38° . Surprisingly enough, this is enough data to fully solve the right triangle! Follow these steps:

• Calculate the third angle: β = 90 ° − α \beta = 90\degree - \alpha β = 90° − α .
• sin ⁡ ( α ) = 0.61567 \sin(\alpha) = 0.61567 sin ( α ) = 0.61567 .
• o p p o s i t e = sin ⁡ ( α ) ⋅ h y p o t e n u s e = 0.61567 ⋅ 5 = 3.078 \mathrm{opposite} = \sin(\alpha)\cdot\mathrm{hypotenuse} = 0.61567 \cdot 5 = 3.078 opposite = sin ( α ) ⋅ hypotenuse = 0.61567 ⋅ 5 = 3.078 .
• a d j a c e n t = 0.788 ⋅ 5 = 3.94 \mathrm{adjacent} = 0.788\cdot 5 = 3.94 adjacent = 0.788 ⋅ 5 = 3.94 .

If you liked our right triangle trigonometry calculator, why not try our other related tools? Here they are:

• The trigonometry calculator ;
• The cosine triangle calculator ;
• The sine triangle calculator ;
• The trig triangle calculator ;
• The trig calculator ;
• The sine cosine tangent calculator ;
• The tangent ratio calculator ; and
• The tangent angle calculator .

How do I apply trigonometry to a right triangle?

To apply trigonometry to a right triangle, remember that sine and cosine correspond to the legs of a right triangle . To solve a right triangle using trigonometry:

• sin(α) = opposite/hypotenuse ; and
• cos(α) = adjacent/hypotenuse .
• By taking the inverse trigonometric functions , we can find the value of the angle α .
• You can repeat the procedure for the other angle.

What is the hypotenuse of a triangle with α = 30° and opposite leg a = 3?

The length of the hypotenuse is 6 . To find this result:

• Calculate the sine of α : sin(α) = sin(30°) = 1/2 .
• Apply the following formula: sin(α) = opposite/hypotenuse hypotenuse = opposite/sin(α) = 3 · 2 = 6 .

Can I apply right-triangle trigonometric rules in a non-right triangle?

Not directly: to apply the relationships between trigonometric functions and sides of a triangle, divide the shape alongside one of the heights lying inside it. This way, you can split the triangle into two right triangles and, with the right combination of data, solve it!

Humans vs vampires

Isosceles triangle, sas triangle.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (184)
• Other (183)
• Discover Omni (40)

Chapter 4.2: Right Triangle Trigonometry

Using right triangle trigonometry to solve applied problems, using trigonometric functions.

In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.

How To: Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides.

• For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
• Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
• Using the value of the trigonometric function and the known side length, solve for the missing side length.

Example 5: Finding Missing Side Lengths Using Trigonometric Ratios

Find the unknown sides of the triangle in Figure 11.

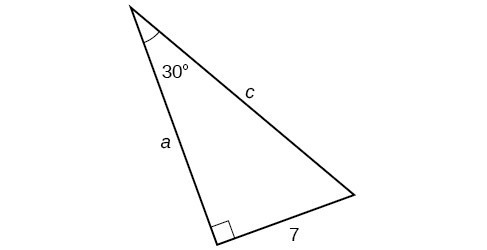
We know the angle and the opposite side, so we can use the tangent to find the adjacent side.

We rearrange to solve for [latex]a[/latex].

We can use the sine to find the hypotenuse.

Again, we rearrange to solve for [latex]c[/latex].

A right triangle has one angle of [latex]\frac{\pi }{3}[/latex] and a hypotenuse of 20. Find the unknown sides and angle of the triangle.

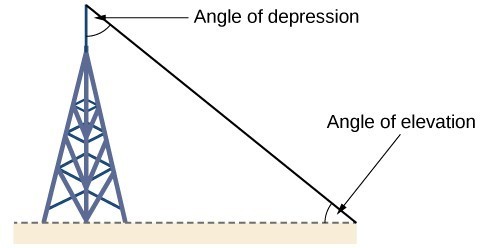
Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer’s eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height. Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer’s eye.

How To: Given a tall object, measure its height indirectly.

• Make a sketch of the problem situation to keep track of known and unknown information.
• Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
• At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
• Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
• Solve the equation for the unknown height.

Example 6: Measuring a Distance Indirectly

To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of [latex]57^\circ [/latex] between a line of sight to the top of the tree and the ground, as shown in Figure 13. Find the height of the tree.

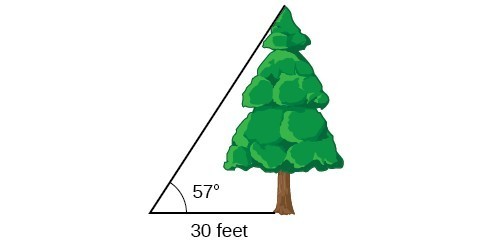
We know that the angle of elevation is [latex]57^\circ [/latex] and the adjacent side is 30 ft long. The opposite side is the unknown height.

The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of [latex]57^\circ [/latex], letting [latex]h[/latex] be the unknown height.

The tree is approximately 46 feet tall.

How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of [latex]\frac{5\pi }{12}[/latex] with the ground? Round to the nearest foot.

• Precalculus. Authored by : OpenStax College. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution
• Example: Determine the Length of a Side of a Right Triangle Using a Trig Equation. Authored by : Mathispower4u. Located at : https://youtu.be/8jU2R3BuR5E . License : All Rights Reserved . License Terms : Standard YouTube License

Solve Right Triangle Problems

Chapter 2: Trigonometric Ratios

2.3 Solving Right Triangles

Algebra refresher.

1. [latex]\:\sqrt{2}\sqrt{2}[/latex]

2. [latex]\:\dfrac{3}{\sqrt{3}}[/latex]

3. [latex]\:\sqrt{8}[/latex]

4. [latex]\:\sqrt{\dfrac{3}{4}}[/latex]

Rationalize the denominator.

5. [latex]\:\dfrac{1}{\sqrt{2}}[/latex]

6. [latex]\:\dfrac{2}{\sqrt{3}}[/latex]

7. [latex]\:\dfrac{6}{\sqrt{3}}[/latex]

8. [latex]\:\dfrac{4}{\sqrt{8}}[/latex]

[latex]\underline{\qquad\qquad\qquad\qquad}[/latex]

• [latex]\displaystyle 2\vphantom{\dfrac{\sqrt{3}}{2}}[/latex]
• [latex]\displaystyle \sqrt{3}\vphantom{\vphantom{\dfrac{\sqrt{3}}{2}}}[/latex]
• [latex]\displaystyle 2\sqrt{2}\vphantom{\dfrac{\sqrt{3}}{2}}[/latex]
• [latex]\displaystyle \dfrac{\sqrt{3}}{2}[/latex]
• [latex]\displaystyle \dfrac{\sqrt{2}}{2}[/latex]
• [latex]\displaystyle \dfrac{2\sqrt{3}}{3}[/latex]
• [latex]\displaystyle 2\sqrt{3}\vphantom{\dfrac{\sqrt{3}}{2}}[/latex]
• [latex]\displaystyle \sqrt{2}\vphantom{\dfrac{\sqrt{3}}{2}}[/latex]

Learning Objectives

• Solve a right triangle
• Use inverse trig ratio notation
• Use trig ratios to find an angle
• Solve problems involving right triangles
• Know the trig ratios for the special angles

Introduction

A triangle has six parts: three sides and three angles. In a right triangle, we know that one of the angles is [latex]90 {^o}\text{.}[/latex] If we know three parts of a right triangle, including one of the sides, we can use trigonometry to find all the other unknown parts. This is called solving the triangle.

Example 2.31.

The hypotenuse of a right triangle is 150 feet long, and one of the angles is [latex]35 {^o}\text{,}[/latex] as shown in the figure. Solve the triangle.

We can find the side opposite the 35° angle by using the sine ratio. [latex]\begin{align*} \sin 35 {^o} = \dfrac {\text{opposite}}{\text{hypotenuse}}\\ 0.5736 = \dfrac{a}{150}\\ a = 150(0.5736) = 86.04 \end{align*}[/latex] The opposite side is about 86 feet long. To find side [latex]b[/latex], we could use the Pythagorean theorem now, but it is better to use given information, rather than values we have calculated, to find the other unknown parts. We will use the cosine ratio. [latex]\begin{align*} \cos 35 {^o} = \dfrac {\text{adjacent}}{\text{hypotenuse}}\\ 0.8192 = \dfrac{b}{150}\\ b = 150(0.8192) = 122.89 \end{align*}[/latex] The adjacent side is about [latex]123[/latex] feet long. Finally, the unknown angle is the complement of [latex]35 {^o}\text{,}[/latex] or [latex]55 {^o}\text{.}[/latex]

Checkpoint 2.32.

Sketch a right triangle with

• one angle of [latex]37 {^o}\text{,}[/latex] and
• the side adjacent to that angle of length 5 centimeters.

Without doing the calculations, list the steps you would use to solve the triangle.

Use tan [latex]37{^o}[/latex] to find the opposite side. Use cos [latex]37{^o}[/latex] to find the hypotenuse. Subtract [latex]37{^o}[/latex] from [latex]90{^o}[/latex] to find the third angle.

Finding an Angle

While watching her niece at the playground, Francine wonders how steep the slide is. She happens to have a tape measure and her calculator with her and finds that the slide is 77 inches high and covers a horizontal distance of 136 inches, as shown below.

Francine knows that one way to describe the steepness of an incline is to calculate its slope, which in this case is [latex]\begin{equation*} \dfrac {\Delta y}{\Delta x} = \dfrac{77}{136} = 0.5662 \end{equation*}[/latex] However, Francine would really like to know what angle the slide makes with the horizontal. She realizes that the slope she has just calculated is also the tangent of the angle she wants.

If we know the tangent of an angle, can we find the angle? Yes, we can: locate the key labeled [latex]\boxed{\text{TAN}^{-1}}[/latex] on your calculator; it is probably the second function above the TAN key. Enter [latex]\qquad\qquad\qquad[/latex] 2nd TAN 0.5662

and you should find that [latex]\begin{equation*} \text{tan}^{-1} 0.5662 = 29.52 {^o}\text{.} \end{equation*}[/latex] This means that [latex]29.52 {^o}[/latex] is the angle whose tangent is [latex]0.5662\text{.}[/latex] We read the notation as “ inverse tangent of [latex]0.5662[/latex] is [latex]29.52[/latex] degrees.”

When we find [latex]\tan^{-1}[/latex] of a number, we are finding an angle whose tangent is that number. Similarly, [latex]\sin^{-1}[/latex] and [latex]cos^{-1}[/latex] are read as “inverse sine” and “inverse cosine.” They find an angle with the given sine or cosine.

Example 2.33.

Find the angle whose sine is [latex]0.6834\text{.}[/latex]

Enter 2nd SIN 0.6834 into your calculator to find [latex]\begin{equation*} \sin^{-1} 0.6834 = 43.11{^o} \end{equation*}[/latex] So [latex]43.11{^o}[/latex] is the angle whose sine is [latex]0.6834\text{.}[/latex] Or we can say that [latex]\begin{equation*} \sin 43.11{^o} = 0.6834 \end{equation*}[/latex] You can check the last equation on your calculator.

In the last example, the two equations:

[latex]\begin{equation*} \sin 43.11{^o} = 0.6834\end{equation*}[/latex]

[latex]\begin{equation*} \sin^{-1} 0.6834 = 43.11{^o}\end{equation*}[/latex]

say the same thing in different ways.

Caution 2.35.

The notation [latex]\sin^{-1} x[/latex] does not mean [latex]\dfrac{1}{\sin x}\text{.}[/latex] It is true that we use negative exponents to indicate reciprocals of numbers; for example, [latex]a^{-1} = \dfrac{1}{a}[/latex] and [latex]3^{-1} = \dfrac{1}{3}\text{.}[/latex] But “sin” by itself is not a variable.

• [latex]\sin^{-1} x[/latex] means “the angle whose sine is [latex]x[/latex]”
• [latex]\dfrac{1}{\sin x}[/latex] means “the reciprocal of the sine of angle [latex]x[/latex]”

(You may recall that [latex]f^{-1}(x)[/latex] denotes the inverse function for [latex]f(x)\text{.}[/latex] We will study trigonometric functions in Chapter 4.)

Checkpoint 2.36.

Write the following fact in two different ways: [latex]68{^o}[/latex] is the angle whose cosine is [latex]0.3746\text{.}[/latex]

[latex]\cos 68{^o} = 0.3746[/latex] or [latex]\cos^{-1}(0.3746) = 68{^o}[/latex]

Example 2.37.

Find the angle of inclination of a hill if you gain [latex]400[/latex] feet in elevation while traveling half a mile.

A sketch of the hill is shown at right. (Recall that [latex]1[/latex] mile [latex]= 5280[/latex] feet.)

[latex]\begin{align*} \sin \theta = \dfrac {400}{2640} = 0.\overline{15}\\ \theta = \sin^{-1} 0.\overline{15} = 8.71{^o} \end{align*}[/latex]

The angle of inclination of the hill is about [latex]8.7{^o}\text{.}[/latex]

Checkpoint 2.38.

The tallest living tree is a coastal redwood named Hyperion, at 378.1 feet tall. If you stand 100 feet from the base of the tree, what is the angle of elevation of your line of sight to the top of the tree? Round your answer to the nearest degree.

[latex]75{^o}[/latex]

The Special Angles

The trigonometric ratios for most angles are irrational numbers, but there are a few angles whose trig ratios are “nice” values. You already know one of these values: the sine of [latex]30{^o}\text{.}[/latex] Because the sides of a right triangle are related by the Pythagorean theorem, if we know any one of the trig ratios for an angle, we can find the others. Recall that the side opposite a [latex]30{^o}[/latex] angle is half the length of the hypotenuse, so [latex]\sin 30{^o} = \dfrac{1}{2}\text{.}[/latex]

The figure at right shows a 30-60-90 triangle with hypotenuse of length [latex]2[/latex]. The opposite side has length 1, and we can calculate the length of the adjacent side. [latex]\begin{align*} 1^2 + b^2 = 2^2 \\ b^2 = 2^2 - 1^2 = 3\\ b = \sqrt{3} \end{align*}[/latex]

Now we know the cosine and tangent of [latex]30{^o}\text{.}[/latex] [latex]\begin{equation*} \cos 30{^o} = \dfrac {\text{adjacent}}{\text{hypotenuse}} = \dfrac{\sqrt{3}}{2} \qquad \tan 30{^o} = \dfrac {\text{opposite}}{\text{adjacent}} = \dfrac{1}{\sqrt{3}} \end{equation*}[/latex]

These are exact values for the trig ratios, but we can also find decimal approximations. Use your calculator to verify the following approximate values. [latex]\begin{align*} \ \ {\text{exact value}} \ \ {\text{approximation}}\\ \cos 30{^o} = \dfrac{\sqrt{3}}{2} \approx 0.8660\\ \tan 30{^o} = \dfrac{1}{\sqrt{3}} \approx 0.5774 \end{align*}[/latex]

Caution 2.39.

It is important for you to understand the difference between exact and approximate values. These decimal approximations, like nearly all the other trig values your calculator gives you, are rounded off. Even if your calculator shows you ten or twelve digits, the values are not exactly correct — although they are quite adequate for most practical calculations!

The angles [latex]30{^o}\text{,}[/latex] [latex]60{^o}\text{,}[/latex] and [latex]45{^o}[/latex] are “special” because we can easily find exact values for their trig ratios and use those exact values to find exact lengths for the sides of triangles with those angles.

Example 2.40.

The sides of an equilateral triangle are [latex]8[/latex] centimeters long. Find the exact length of the triangle’s altitude, [latex]h\text{.}[/latex]

The altitude divides the triangle into two 30-60-90 right triangles as shown in the figure. The altitude is adjacent to the [latex]30{^o}[/latex] angle, and the hypotenuse of the right triangle is 8 centimeters. Thus,

[latex]\begin{align*} \cos 35 {^o} = \dfrac {\text{adjacent}}{\text{hypotenuse}} \ \ {\text{Fill in the values.}}\\ \dfrac{\sqrt{3}}{2} = \dfrac{h}{8} \ \ {\text{Multiply both sides by 8.}}\\ h = 8\left(\dfrac{\sqrt{3}}{2}\right) = 4\sqrt{3} \end{align*}[/latex] The altitude is exactly [latex]4\sqrt{3}[/latex] centimeters long.

From this exact answer, we can find approximations to any degree of accuracy we like. You can check that [latex]4\sqrt{3} \approx6.9282\text{,}[/latex] so the altitude is approximately 6.9 centimeters long.

Checkpoint 2.41.

Use the figure in the previous example to find exact values for the sine, cosine, and tangent of [latex]60{^o}\text{.}[/latex]

[latex]\sin 60{^o} = \dfrac{\sqrt{3}}{2}\text{,}[/latex] [latex]\cos 60{^o} = \dfrac{1}{2}\text{,}[/latex] [latex]\tan 60{^o} = \sqrt{3}[/latex]

There is one more special angle: [latex]45{^o}\text{.}[/latex] We find the trig ratios for this angle using an isosceles right triangle. Because the base angles of an isosceles triangle are equal, they must both be [latex]45{^o}\text{.}[/latex] The figure shows an isosceles right triangle with equal sides of length 1. You can use the Pythagorean theorem to show that the hypotenuse has length [latex]\sqrt{2}\text{,}[/latex] so the trig ratios for [latex]45{^o}[/latex] are[latex]\begin{align*} \sin 45{^o} = \dfrac {\text{opposite}}{\text{hypotenuse}} = \dfrac{1}{\sqrt{2}} \approx 0.7071\\ \cos 45{^o} = \dfrac {\text{adjacent}}{\text{hypotenuse}} = \dfrac{1}{\sqrt{2}} \approx 0.7071\\ \tan 45{^o} = \dfrac {\text{opposite}}{\text{adjacent}} = 1 \end{align*}[/latex]

The Trigonometric Ratios for the Special Angles

Here is a summary of the trig ratios for the special angles.

You should memorize the exact values for these trig ratios. A good way to remember them is to know the two special triangles shown below. From these triangles, you can always write down the three trig ratios for the special angles.

You should also be able to recognize their decimal approximations.

We can use the special angles as benchmarks for estimating and mental calculation. For example, we know that [latex]60{^o} \approx 0.8660\text{,}[/latex] so if sin [latex]\theta = 0.95[/latex] for some unknown angle [latex]\theta\text{,}[/latex] we know that [latex]\theta \gt 60{^o}\text{,}[/latex] because as [latex]\theta[/latex] increases from the sine of [latex]\theta[/latex] increases also.

Example 2.43.

If [latex]\cos \alpha \gt \dfrac{\sqrt{3}}{2}\text{,}[/latex] what can we say about [latex]\alpha\text{?}[/latex]

As an angle increases from [latex]0{^o}[/latex] to [latex]90{^o}\text{,}[/latex] its cosine decreases. Now, [latex]\cos 30{^o} = \dfrac{\sqrt{3}}{2}\text{,}[/latex] so if [latex]\cos \alpha \gt \dfrac{\sqrt{3}}{2}\text{,}[/latex] then [latex]\alpha[/latex] must be less than [latex]30{^o}\text{.}[/latex]

Checkpoint 2.44.

If [latex]1 \lt \tan \beta \lt \sqrt{3}\text{,}[/latex] what can we say about [latex]\beta\text{?}[/latex]

[latex]45{^o} \lt \beta \lt 60{^o}[/latex]

Section 2.3 Summary

• Solve a triangle
• Inverse sine
• Inverse cosine
• Inverse tangent
• Special angles
• Exact value
• Decimal approximation
• If we know one of the sides of a right triangle and any one of the other four parts, we can use trigonometry to find all the other unknown parts.
• If we know one of the trigonometric ratios of an acute angle, we can find the angle using the inverse trig key on a calculator.
• For the trigonometric ratios of most angles, your calculator gives approximations, not exact values.

Study Questions

• How many parts of a right triangle (including the right angle) do you need to know in order to solve the triangle?
• Why is it better to use the given values, rather than values you have calculated, when solving a triangle?
• What is the [latex]\sin^{-1}[/latex] (or [latex]\cos^{-1}[/latex] or [latex]\tan^{-1}[/latex]) button on the calculator used for?
• Which are the “special” angles, and why are they special?

If we know three parts of a right triangle, including one of the sides, we can use trigonometry to find all the other unknown parts. This is called solving the triangle.

The inverse sine (arcsine) of a value is the angle whose sine is equal to that value.

The inverse cosine (arccosine) of a value is the angle whose sine is equal to that value.

The inverse tangent (arctangent) of a value is the angle whose sine is equal to that value.

Special angles in trigonometry are angles whose sine, cosine, and tangent values can be calculated exactly without the use of a calculator.

An exact value for a trigonometric function is a value that can be represented as a finite combination of integers, radicals, and/or known mathematical constants without the use of a calculator or approximations.

A decimal approximation for a trigonometric function is an estimation of its value expressed as a finite string of decimal digits, usually rounded to a certain number of decimal places, and obtained through the use of a calculator or other computational tool.

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

Trigonometry : Solving Word Problems with Trigonometry

Study concepts, example questions & explanations for trigonometry, all trigonometry resources, example questions, example question #1 : solving word problems with trigonometry.

You can draw the following right triangle using the information given by the question:

Since you want to find the height of the platform, you will need to use tangent.

You can draw the following right triangle from the information given by the question.

In order to find the height of the flagpole, you will need to use tangent.

You can draw the following right triangle from the information given in the question:

In order to find out how far up the ladder goes, you will need to use sine.

In right triangle ABC, where angle A measures 90 degrees, side AB measures 15 and side AC measures 36, what is the length of side BC?

This triangle cannot exist.

Example Question #5 : Solving Word Problems With Trigonometry

A support wire is anchored 10 meters up from the base of a flagpole, and the wire makes a 25 o angle with the ground. How long is the wire, w? Round your answer to two decimal places.

23.81 meters

28.31 meters

21.83 meters

To make sense of the problem, start by drawing a diagram. Label the angle of elevation as 25 o , the height between the ground and where the wire hits the flagpole as 10 meters, and our unknown, the length of the wire, as w. 

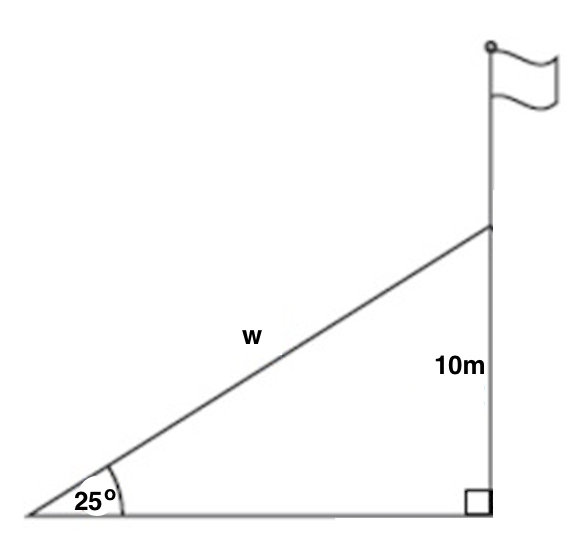
Now, we just need to solve for w using the information given in the diagram. We need to ask ourselves which parts of a triangle 10 and w are relative to our known angle of 25 o . 10 is opposite this angle, and w is the hypotenuse. Now, ask yourself which trig function(s) relate opposite and hypotenuse. There are two correct options: sine and cosecant. Using sine is probably the most common, but both options are detailed below.

We know that sine of a given angle is equal to the opposite divided by the hypotenuse, and cosecant of an angle is equal to the hypotenuse divided by the opposite (just the reciprocal of the sine function). Therefore:

To solve this problem instead using the cosecant function, we would get:

The reason that we got 23.7 here and 23.81 above is due to differences in rounding in the middle of the problem. 

Example Question #6 : Solving Word Problems With Trigonometry

When the sun is 22 o above the horizon, how long is the shadow cast by a building that is 60 meters high?

To solve this problem, first set up a diagram that shows all of the info given in the problem. 

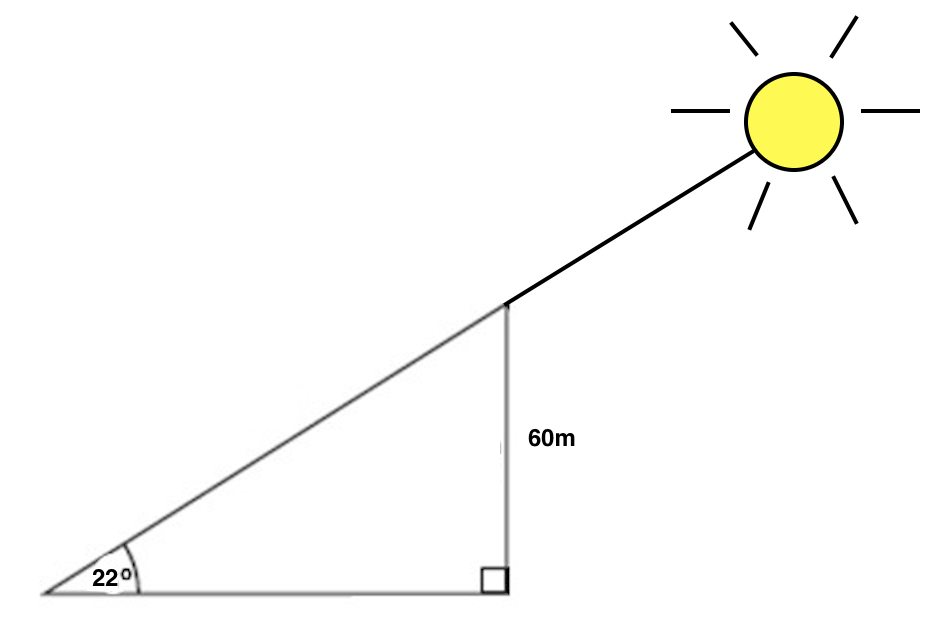
Next, we need to interpret which side length corresponds to the shadow of the building, which is what the problem is asking us to find. Is it the hypotenuse, or the base of the triangle? Think about when you look at a shadow. When you see a shadow, you are seeing it on something else, like the ground, the sidewalk, or another object. We see the shadow on the ground, which corresponds to the base of our triangle, so that is what we'll be solving for. We'll call this base b.

Therefore the shadow cast by the building is 150 meters long.

If you got one of the incorrect answers, you may have used sine or cosine instead of tangent, or you may have used the tangent function but inverted the fraction (adjacent over opposite instead of opposite over adjacent.)

Example Question #7 : Solving Word Problems With Trigonometry

From the top of a lighthouse that sits 105 meters above the sea, the angle of depression of a boat is 19 o . How far from the boat is the top of the lighthouse?

423.18 meters

318.18 meters

36.15 meters

110.53 meters

To solve this problem, we need to create a diagram, but in order to create that diagram, we need to understand the vocabulary that is being used in this question. The following diagram clarifies the difference between an angle of depression (an angle that looks downward; relevant to our problem) and the angle of elevation (an angle that looks upward; relevant to other problems, but not this specific one.) Imagine that the top of the blue altitude line is the top of the lighthouse, the green line labelled GroundHorizon is sea level, and point B is where the boat is.

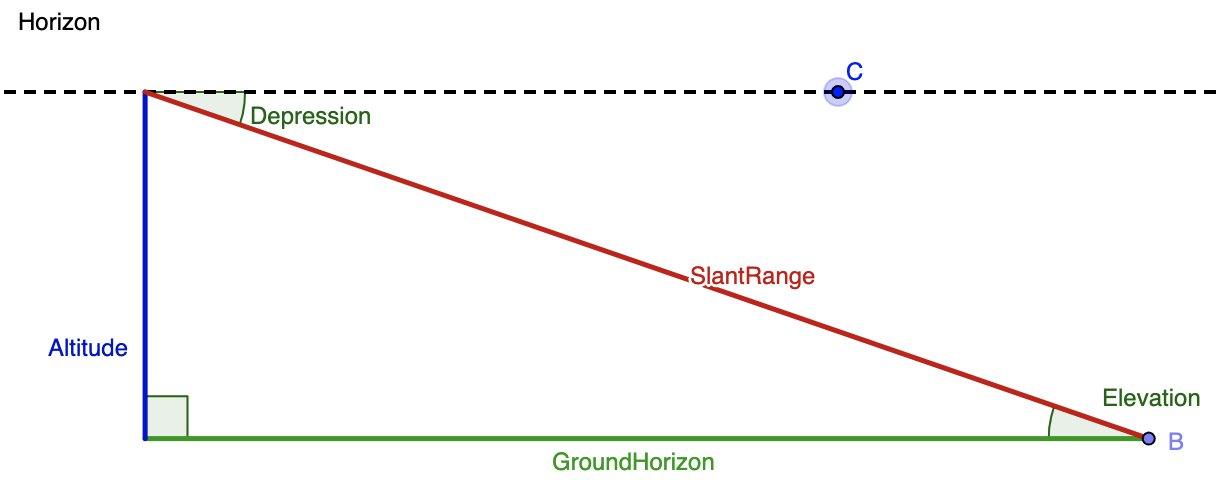
Merging together the given info and this diagram, we know that the angle of depression is 19 o  and and the altitude (blue line) is 105 meters. While the blue line is drawn on the left hand side in the diagram, we can assume is it is the same as the right hand side. Next, we need to think of the trig function that relates the given angle, the given side, and the side we want to solve for. The altitude or blue line is opposite the known angle, and we want to find the distance between the boat (point B) and the top of the lighthouse. That means that we want to determine the length of the hypotenuse, or red line labelled SlantRange. The sine function relates opposite and hypotenuse, so we'll use that here. We get:

Example Question #8 : Solving Word Problems With Trigonometry

Angelina just got a new car, and she wants to ride it to the top of a mountain and visit a lookout point. If she drives 4000 meters along a road that is inclined 22 o to the horizontal, how high above her starting point is she when she arrives at the lookout?

9.37 meters

1480 meters

3708.74 meters

10677.87 meters

1616.1 meters

As with other trig problems, begin with a sketch of a diagram of the given and sought after information.

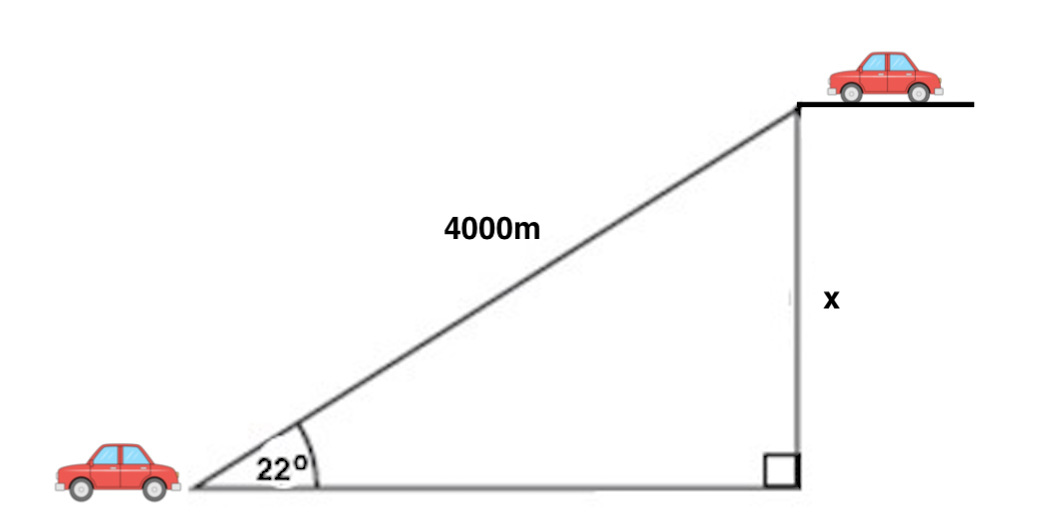
Angelina and her car start at the bottom left of the diagram. The road she is driving on is the hypotenuse of our triangle, and the angle of the road relative to flat ground is 22 o . Because we want to find the change in height (also called elevation), we want to determine the difference between her ending and starting heights, which is labelled x in the diagram. Next, consider which trig function relates together an angle and the sides opposite and hypotenuse relative to it; the correct one is sine. Then, set up:

Therefore the change in height between Angelina's starting and ending points is 1480 meters. 

Example Question #9 : Solving Word Problems With Trigonometry

Two buildings with flat roofs are 50 feet apart. The shorter building is 40 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 48 o . How high is the taller building?

To solve this problem, let's start by drawing a diagram of the two buildings, the distance in between them, and the angle between the tops of the two buildings. Then, label in the given lengths and angle. 

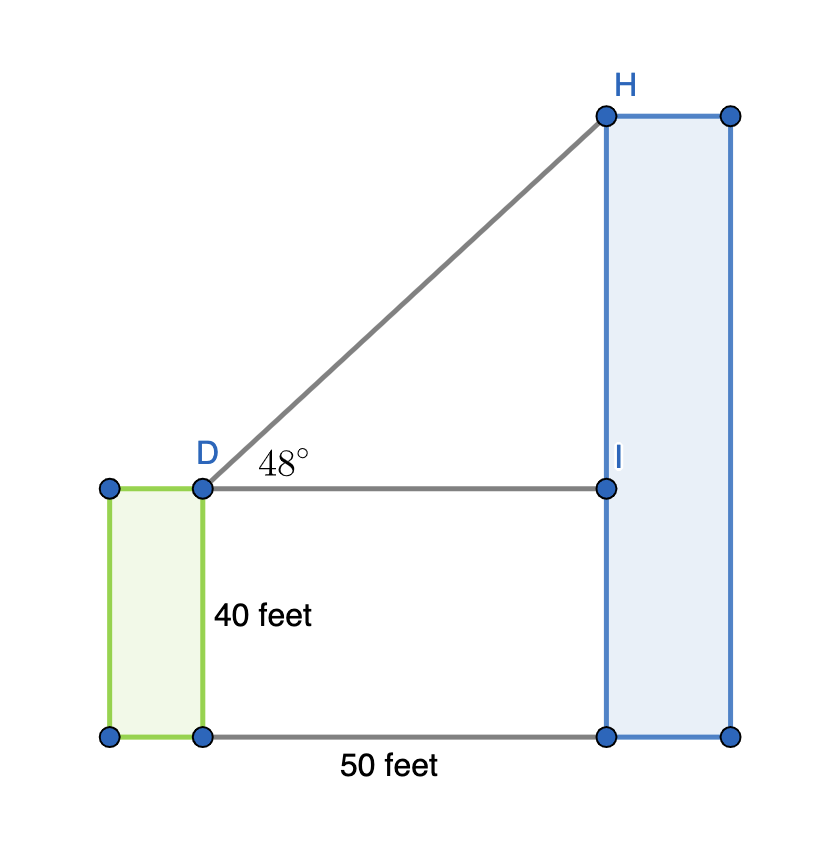
Example Question #10 : Solving Word Problems With Trigonometry

Two buildings with flat roofs are 80 feet apart. The shorter building is 55 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 32 o . How high is the taller building?

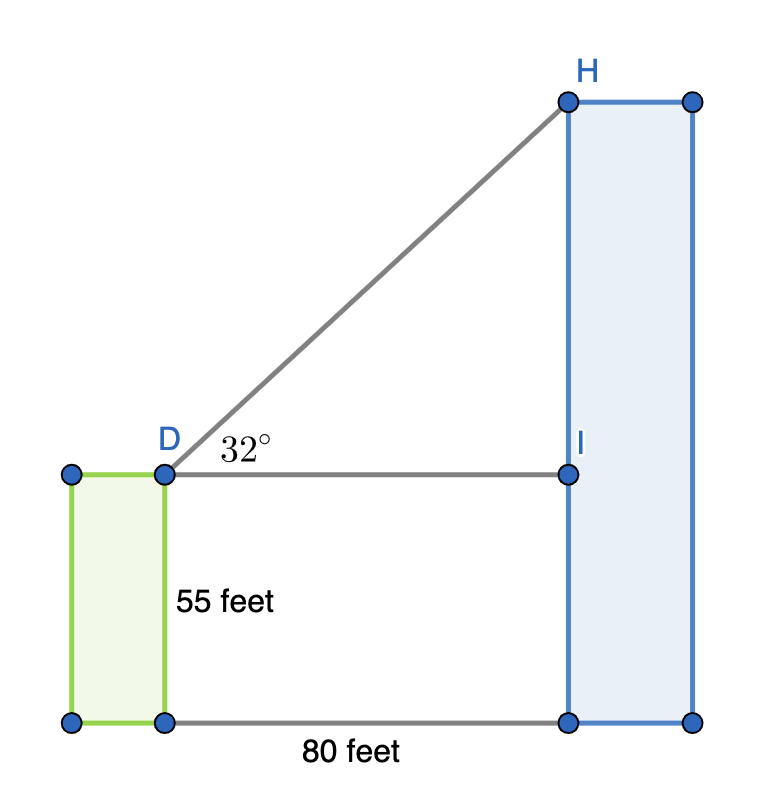
Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.3: Applications and Solving Right Triangles

• Last updated
• Save as PDF
• Page ID 3246

• Michael Corral
• Schoolcraft College

Throughout its early development, trigonometry was often used as a means of indirect measurement, e.g. determining large distances or lengths by using measurements of angles and small, known distances. Today, trigonometry is widely used in physics, astronomy, engineering, navigation, surveying, and various fields of mathematics and other disciplines. In this section we will see some of the ways in which trigonometry can be applied. Your calculator should be in degree mode for these examples.

Example 1.11

A person stands \(150\) ft away from a flagpole and measures an angle of elevation of \(32^\circ\) from his horizontal line of sight to the top of the flagpole. Assume that the person's eyes are a vertical distance of 6 ft from the ground. What is the height of the flagpole?

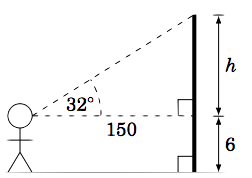
The picture on the right describes the situation. We see that the height of the flagpole is \(h + 6\) ft, where

\[\frac{h}{150} ~=~ \tan\;32^\circ \quad\Rightarrow\quad h ~=~ 150\;\tan\;32^\circ ~=~ 150\;(0.6249) ~=~ 94 ~. \nonumber \]

How did we know that \(\tan\;32^\circ = 0.6249\,\)? By using a calculator. And since none of the numbers we were given had decimal places, we rounded off the answer for \(h\) to the nearest integer. Thus, the height of the flagpole is \(\,h + 6 = 94 + 6 = \boxed{100 ~\text{ft}}\).

Example 1.12

A person standing \(400\) ft from the base of a mountain measures the angle of elevation from the ground to the top of the mountain to be \(25^\circ \). The person then walks \(500\) ft straight back and measures the angle of elevation to now be \(20^\circ \). How tall is the mountain?

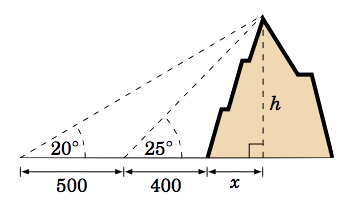
We will assume that the ground is flat and not inclined relative to the base of the mountain. Let \(h\) be the height of the mountain, and let \(x\) be the distance from the base of the mountain to the point directly beneath the top of the mountain, as in the picture on the right. Then we see that

\[ \begin{align*} \frac{h}{x + 400} ~=~ \tan\;25^\circ \quad &\Rightarrow \quad h ~=~ (x + 400)\;\tan\;25^\circ ~,~\text{and}\\[4pt] \frac{h}{x + 400 + 500} ~=~ \tan\;20^\circ \quad &\Rightarrow \quad h ~=~ (x + 900)\;\tan\;20^\circ, \end{align*} \nonumber \]

\((x + 400)\;\tan\;25^\circ ~=~ (x + 900)\;\tan\;20^\circ \), since they both equal \(h \). Use that equation to solve for \(x\):

\[ x\;\tan\;25^\circ ~-~ x\;\tan\;20^\circ ~=~ 900\;\tan\;20^\circ ~-~ 400\;\tan\;25^\circ \quad\Rightarrow\quad x ~=~ \frac{900\;\tan\;20^\circ ~-~ 400\;\tan\;25^\circ}{\tan\;25^\circ ~-~ \tan\;20^\circ} ~=~ 1378~ \text{ft} \nonumber \]

Finally, substitute \(x\) into the first formula for \(h\) to get the height of the mountain:

\[h ~=~ (1378 + 400)\;\tan\;25^\circ ~=~ 1778\;(0.4663) ~=~ \boxed{829~ \text{ft}} \nonumber \]

Example 1.13

A blimp \(4280\) ft above the ground measures an angle of depression of \(24^\circ\) from its horizontal line of sight to the base of a house on the ground. Assuming the ground is flat, how far away along the ground is the house from the blimp?

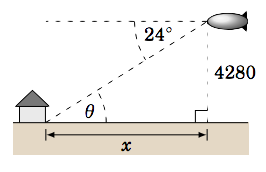
Let \(x\) be the distance along the ground from the blimp to the house, as in the picture to the right. Since the ground and the blimp's horizontal line of sight are parallel, we know from elementary geometry that the angle of elevation \(\theta\) from the base of the house to the blimp is equal to the angle of depression from the blimp to the base of the house, i.e. \(\theta = 24^\circ \). Hence,

\[\frac{4280}{x} ~=~ \tan\;24^\circ \quad\Rightarrow\quad x ~=~ \frac{4280}{\tan\;24^\circ} ~=~ \boxed{9613 ~\text{ft}}~. \nonumber \]

Example 1.14

An observer at the top of a mountain \(3\) miles above sea level measures an angle of depression of \(2.23^\circ\) to the ocean horizon. Use this to estimate the radius of the earth.

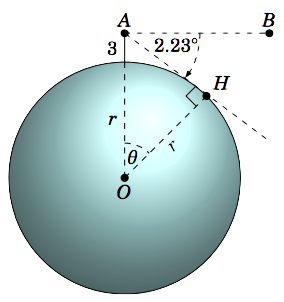
We will assume that the earth is a sphere. Let \(r\) be the radius of the earth. Let the point \(A\) represent the top of the mountain, and let \(H\) be the ocean horizon in the line of sight from \(A \), as in Figure 1.3.1. Let \(O\) be the center of the earth, and let \(B\) be a point on the horizontal line of sight from \(A\) (i.e. on the line perpendicular to \(\overline{OA}\)). Let \(\theta\) be the angle \(\angle\,AOH \).

Since \(A\) is \(3\) miles above sea level, we have \(OA = r + 3 \). Also, \(OH = r \). Now sincev\(\overline{AB} \perp \overline{OA} \), we have \(\angle\,OAB = 90^\circ \), so we see that \(\angle\,OAH = 90^\circ - 2.23^\circ = 87.77^\circ \). We see that the line through \(A\) and \(H\) is a tangent line to the surface of the earth (considering the surface as the circle of radius \(r\) through \(H\) as in the picture). So by Exercise 14 in Section 1.1, \(\overline{AH} \perp \overline{OH}\) and hence \(\angle\,OHA = 90^\circ \). Since the angles in the triangle \(\triangle\,OAH\) add up to \(180^\circ \), we have \(\theta = 180^\circ - 90^\circ - 87.77^\circ = 2.23^\circ \). Thus,

\[\cos\;\theta ~=~ \frac{OH}{OA} ~=~ \frac{r}{r+3} \quad\Rightarrow\quad \frac{r}{r+3} ~=~ \cos\;2.23^\circ ~, \nonumber \]

so solving for \(r\) we get

\[\begin{align*} r ~=~ (r ~+~ 3)\;\cos\;2.23^\circ \quad &\Rightarrow \quad r ~-~ r\;\cos\;2.23^\circ ~=~ 3\;\cos\;2.23^\circ \\[4pt] &\Rightarrow \quad r ~=~ \frac{3\;\cos\;2.23^\circ}{1 ~-~ \cos\;2.23^\circ}\\ &\Rightarrow \quad \boxed{r ~=~ 3958.3 ~\text{miles}} ~. \end{align*} \nonumber \]

Note: This answer is very close to the earth's actual (mean) radius of \(3956.6\) miles.

Example 1.15

As another application of trigonometry to astronomy, we will find the distance from the earth to the sun. Let \(O\) be the center of the earth, let \(A\) be a point on the equator, and let \(B\) represent an object (e.g. a star) in space, as in the picture on the right. If the earth is positioned in such a way that the angle \(\angle\,OAB = 90^\circ \), then we say that the angle \(\alpha = \angle\,OBA\) is the equatorial parallax of the object. The equatorial parallax of the sun has been observed to be approximately \(\alpha =0.00244^\circ \). Use this to estimate the distance from the center of the earth to the sun.

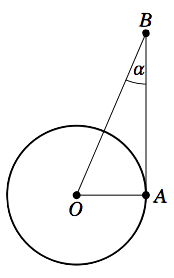
Let \(B\) be the position of the sun. We want to find the length of \(\overline{OB} \). We will use the actual radius of the earth, mentioned at the end of Example 1.14, to get \(OA = 3956.6\) miles. Since \(\angle\,OAB = 90^\circ \), we have

\[\frac{OA}{OB} ~=~ \sin\;\alpha \quad\Rightarrow\quad OB ~=~ \frac{OA}{\sin\;\alpha} ~=~ \frac{3956.6}{\sin\;0.00244^\circ} ~=~ 92908394 ~, \nonumber \]

so the distance from the center of the earth to the sun is approximately \(\fbox{\(93\) million miles}~.\)

Note: The earth's orbit around the sun is an ellipse, so the actual distance to the sun varies.

In the above example we used a very small angle (\(0.00244^\circ\)). A degree can be divided into smaller units: a minute is one-sixtieth of a degree, and a second is one-sixtieth of a minute. The symbol for a minute is \('\) and the symbol for a second is \('' \). For example, \(4.5^\circ = 4^\circ\;30' \). And \(4.505^\circ = 4^\circ\;30'\;18''\):

\[4^\circ\;30'\;18'' ~=~ 4 ~+~ \frac{30}{60} ~+~ \frac{18}{3600} ~\text{degrees} ~=~ 4.505^\circ \nonumber \]

In Example 1.15 we used \(\alpha = 0.00244^\circ \approx 8.8'' \), which we mention only because some angle measurement devices do use minutes and seconds.

Example 1.16

An observer on earth measures an angle of \(32'\;4''\) from one visible edge of the sun to the other (opposite) edge, as in the picture on the right. Use this to estimate the radius of the sun.

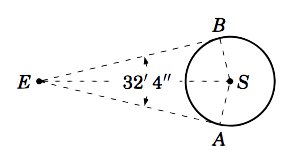
Let the point \(E\) be the earth and let \(S\) be the center of the sun. The observer's lines of sight to the visible edges of the sun are tangent lines to the sun's surface at the points \(A\) and \(B \). Thus, \(\angle\,EAS = \angle\,EBS = 90^\circ \). The radius of the sun equals \(AS \). Clearly \(AS = BS \). So since \(EB = EA\) (why?), the triangles \(\triangle\,EAS\) and \(\triangle\,EBS\) are similar. Thus, \(\angle\,AES = \angle\,BES = \frac{1}{2}\; \angle\,AEB = \frac{1}{2}\;(32'\;4'') = 16'\;2'' = (16/60) + (2/3600) = 0.26722^\circ \).

Now, \(ES\) is the distance from the surface of the earth (where the observer stands) to the center of the sun. In Example 1.15 we found the distance from the center of the earth to the sun to be \(92,908,394\) miles. Since we treated the sun in that example as a point, then we are justified in treating that distance as the distance between the centers of the earth and sun. So \(ES = 92908394 - ~\text{radius of earth} = 92908394 - 3956.6 = 92904437.4\) miles. Hence,

\[\sin\;(\angle\,AES) ~=~ \frac{AS}{ES} \quad\Rightarrow\quad AS ~=~ ES \;\sin\;0.26722^\circ ~=~ (92904437.4)\;\sin\;0.26722^\circ ~=~ \boxed{433,293 ~\text{miles}} ~. \nonumber \]

Note: This answer is close to the sun's actual (mean) radius of \(432,200\) miles.

You may have noticed that the solutions to the examples we have shown required at least one right triangle. In applied problems it is not always obvious which right triangle to use, which is why these sorts of problems can be difficult. Often no right triangle will be immediately evident, so you will have to create one. There is no general strategy for this, but remember that a right triangle requires a right angle, so look for places where you can form perpendicular line segments. When the problem contains a circle, you can create right angles by using the perpendicularity of the tangent line to the circle at a point with the line that joins that point to the center of the circle. We did exactly that in Examples 1.14, 1.15, and 1.16.

Example 1.17

The machine tool diagram on the right shows a symmetric V-block , in which one circular roller sits on top of a smaller circular roller. Each roller touches both slanted sides of the V-block. Find the diameter \(d\) of the large roller, given the information in the diagram.

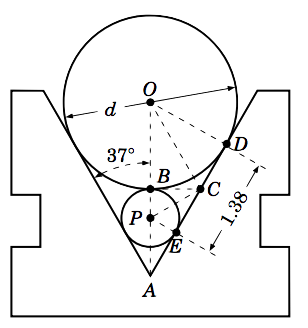
The diameter \(d\) of the large roller is twice the radius \(OB \), so we need to find \(OB \). To do this, we will show that \(\triangle\,OBC\) is a right triangle, then find the angle \(\angle\,BOC \), and then find \(BC \). The length \(OB\) will then be simple to determine.

Since the slanted sides are tangent to each roller, \(\angle\,ODA = \angle\,PEC =90^\circ \). By symmetry, since the vertical line through the centers of the rollers makes a \(37^\circ\) angle with each slanted side, we have \(\angle\,OAD = 37^\circ \). Hence, since \(\triangle\,ODA\) is a right triangle, \(\angle\,DOA\) is the complement of \(\angle\,OAD \). So \(\angle\,DOA = 53^\circ \).

Since the horizontal line segment \(\overline{BC}\) is tangent to each roller, \(\angle\,OBC =\angle\,PBC = 90^\circ \). Thus, \(\triangle\,OBC\) is a right triangle. And since \(\angle\,ODA = 90^\circ \), we know that \(\triangle\,ODC\) is a right triangle. Now, \(OB = OD\) (since they each equal the radius of the large roller), so by the Pythagorean Theorem we have \(BC = DC\):

\[BC^2 ~=~ OC^2 ~-~ OB^2 ~=~ OC^2 ~-~ OD^2 ~=~ DC^2 \quad\Rightarrow\quad BC ~=~ DC \nonumber \]

Thus, \(\triangle\,OBC\) and \(\triangle\,ODC\) are congruent triangles (which we denote by \(\triangle\,OBC \cong \triangle\,ODC\)), since their corresponding sides are equal. Thus, their corresponding angles are equal. So in particular, \(\angle\,BOC = \angle\,DOC \). We know that \(\angle\,DOB = \angle\,DOA = 53^\circ \). Thus,

\[53^\circ ~=~ \angle\,DOB ~=~ \angle\,BOC ~+~ \angle\,DOC = \angle\,BOC ~+~ \angle\,BOC ~=~ 2\;\angle\,BOC \quad\Rightarrow\quad \angle\,BOC ~=~ 26.5^\circ ~. \nonumber \]

Likewise, since \(BP = EP\) and \(\angle\,PBC = \angle\,PEC = 90^\circ \), \(\triangle\,BPC\) and \(\triangle\,EPC\) are congruent right triangles. Thus, \(BC = EC \). But we know that \(BC = DC \), and we see from the diagram that \(EC + DC = 1.38 \). Thus, \(BC + BC = 1.38\) and so \(BC = 0.69 \). We now have all we need to find \(OB\):

\[\frac{BC}{OB} ~=~ \tan\;\angle\,BOC \quad\Rightarrow\quad OB ~=~ \frac{BC}{\tan\;\angle\,BOC} ~=~ \frac{0.69}{\tan\;26.5^\circ} ~=~ 1.384 \nonumber \]

Hence, the diameter of the large roller is \(\,d = 2 \times OB = 2\,(1.384) = \boxed{2.768}\)~.

Example 1.18

A slider-crank mechanism is shown in Figure 1.3.2 below. As the piston moves downward the connecting rod rotates the crank in the clockwise direction, as indicated.

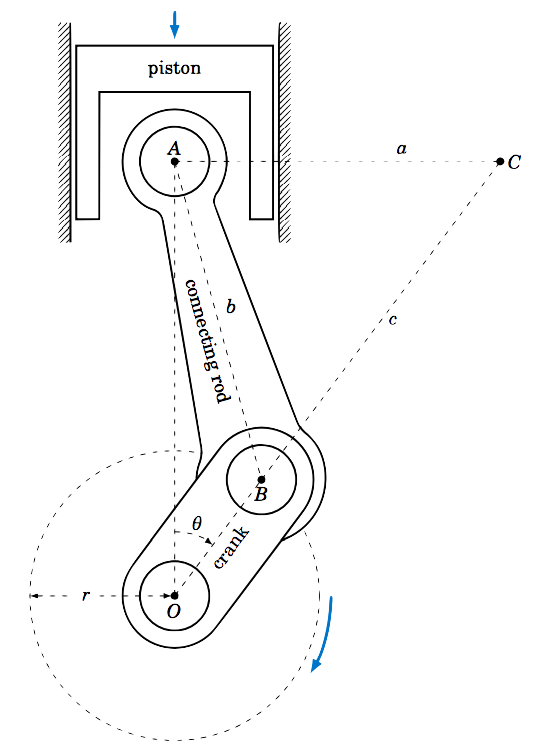
The point \(A\) is the center of the connecting rod's wrist pin and only moves vertically. The point \(B\) is the center of the crank pin and moves around a circle of radius \(r\) centered at the point \(O \), which is directly below \(A\) and does not move. As the crank rotates it makes an angle \(\theta\) with the line \(\overline{OA} \). The instantaneous center of rotation of the connecting rod at a given time is the point \(C\) where the horizontal line through \(A\) intersects the extended line through \(O\) and \(B \). From Figure 1.3.2 we see that \(\angle\,OAC = 90^\circ \), and we let \(a = AC \), \(b = AB \), and \(c = BC \). In the exercises you will show that for \(0^\circ < \theta < 90^\circ \),

\[c ~=~ \frac{\sqrt{b^2 ~-~ r^2 \;(\sin\,\theta)^2}}{\cos\;\theta} ~\qquad\text{and}\qquad~ a ~=~ r\;\sin\;\theta ~+~ \sqrt{b^2 ~-~ r^2 \;(\sin\,\theta)^2}~\tan\;\theta ~. \nonumber \]

For some problems it may help to remember that when a right triangle has a hypotenuse of length \(r\) and an acute angle \(\theta \), as in the picture below, the adjacent side will have length \(r\,\cos\;\theta\) and the opposite side will have length \(r\,\sin\;\theta \). You can think of those lengths as the horizontal and vertical ``components'' of the hypotenuse.

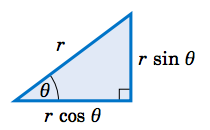
Notice in the above right triangle that we were given two pieces of information: one of the acute angles and the length of the hypotenuse. From this we determined the lengths of the other two sides, and the other acute angle is just the complement of the known acute angle. In general, a triangle has six parts: three sides and three angles. Solving a triangle means finding the unknown parts based on the known parts. In the case of a right triangle, one part is always known: one of the angles is \(90^\circ \).

Example 1.19

Solve the right triangle in Figure 1.3.3 using the given information:

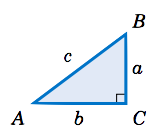
(a) \(c = 10,\, A = 22^◦\) Solution : The unknown parts are \(a \), \(b \), and \(B \). Solving yields:

\[\begin{align} a ~ &= ~ c\;\sin\;A ~ &= ~ 10\;\sin\;22^\circ ~ &= ~ 3.75\\ b ~ &= ~ c\;\cos\;A ~ &= ~ 10\;\cos\;22^\circ ~ &= ~ 9.27\\ B ~ &= ~ 90^\circ ~-~ A ~ &= ~ 90^\circ ~-~ 22^\circ ~ &= ~ 68^\circ \end{align} \nonumber \]

(b) \(b = 8,\, A = 40^◦\) Solution : The unknown parts are \(a \), \(c \), and \(B \). Solving yields:

\[\begin{align}\frac{a}{b} ~ &= ~ \tan\;A \quad &\Rightarrow \quad a ~ &= ~ b\;\tan\;A ~ = ~8\;\tan\;40^\circ ~ = ~ 6.71\\\frac{b}{c} ~ &= ~ \cos\;A \quad &\Rightarrow \quad c ~ &= ~ \frac{b}{\cos\;A} ~ = ~\frac{8}{\cos\;40^\circ} ~ = ~ 10.44\end{align} \nonumber \]

(c) \(a = 3,\, b = 4\)

Solution : The unknown parts are \(c \), \(A \), and \(B \). By the Pythagorean Theorem,

\[c ~=~ \sqrt{a^2 ~+~ b^2} ~=~ \sqrt{3^2 ~+~ 4^2} ~=~ \sqrt{25} ~=~ 5 ~. \nonumber \]

Now, \(\tan\;A = \frac{a}{b} = \frac{3}{4} = 0.75 \). So how do we find \(A\)? There should be a key labeled \(\fbox{\(\tan^{-1}\)}\) on your calculator, which works like this: give it a number \(x\) and it will tell you the angle \(\theta\) such that \(\tan\;\theta = x \). In our case, we want the angle \(A\) such that \(\tan\;A = 0.75\):

\[ \text{Enter: } 0.75 \quad \text{Press:}\fbox{\(\tan^{-1}\)} \quad \text{Answer: } 36.86989765 \nonumber \]

This tells us that \(A = 36.87^\circ \), approximately. Thus \(B = 90^\circ - A = 90^\circ - 36.87^\circ = 53.13^\circ \).

Note: The \(\fbox{ \(\sin^{-1}\)}\) and \(\fbox{ \(\cos^{-1}\)}\) keys work similarly for sine and cosine, respectively. These keys use the inverse trigonometric functions , which we will discuss in Chapter 5.