assignment 11 absolute value

Chapter 3 Functions

3.7 Absolute Value Functions

Learning objectives.

In this section, you will:

• Graph an absolute value function.
• Solve an absolute value equation.

Until the 1920s, the so-called spiral nebulae were believed to be clouds of dust and gas in our own galaxy, some tens of thousands of light-years away. Then, astronomer Edwin Hubble proved that these objects are galaxies in their own right, at distances of millions of light years. Today, astronomers can detect galaxies that are billions of light years away. Distances in the universe can be measured in all directions. As such, it is useful to consider distance as an absolute value function. In this section, we will continue our investigation of absolute value functions .

Understanding Absolute Value

Recall that in its basic form [latex]\,f\left(x\right)=|x|,\,[/latex] the absolute value function is one of our toolkit functions. The absolute value function is commonly thought of as providing the distance the number is from zero on a number line. Algebraically, for whatever the input value is, the output is the value without regard to sign. Knowing this, we can use absolute value functions to solve some kinds of real-world problems.

Absolute Value Function

The absolute value function can be defined as a piecewise function:

Using Absolute Value to Determine Resistance

Electrical parts, such as resistors and capacitors, come with specified values of their operating parameters: resistance, capacitance, etc. However, due to imprecision in manufacturing, the actual values of these parameters vary somewhat from piece to piece, even when they are supposed to be the same. The best that manufacturers can do is to try to guarantee that the variations will stay within a specified range, often[latex]\,\text{±1%,}\,±\text{5%,}\,[/latex]or[latex]\,±\text{10%}\text{.}[/latex]

Suppose we have a resistor rated at 680 ohms,[latex]\,±\text{5%}\,[/latex].  Use the absolute value function to express the range of possible values of the actual resistance.

We can find that 5% of 680 ohms is 34 ohms. The absolute value of the difference between the actual and nominal resistance should not exceed the stated variability, so with the resistance [latex]\,R\,[/latex] in ohms,

Students who score within 20 points of 80 will pass a test. Write this as a distance from 80 using absolute value notation.

Using the variable[latex]\,p\,[/latex] for passing, [latex]\,|p-80|\le 20[/latex]

Graphing an Absolute Value Function

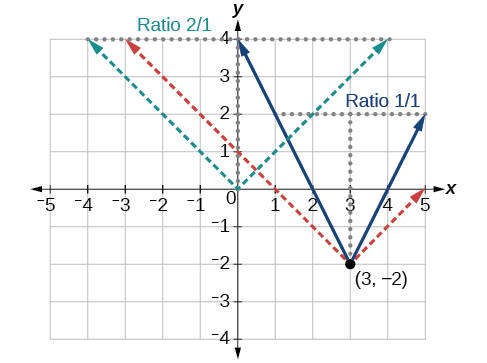
The most significant feature of the absolute value graph is the corner point at which the graph changes direction. This point is shown at the origin in Figure 2.

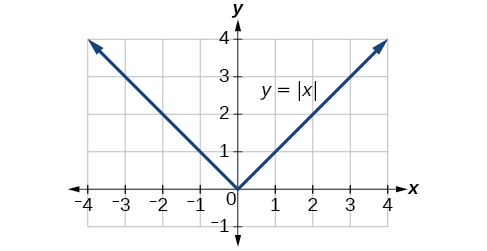
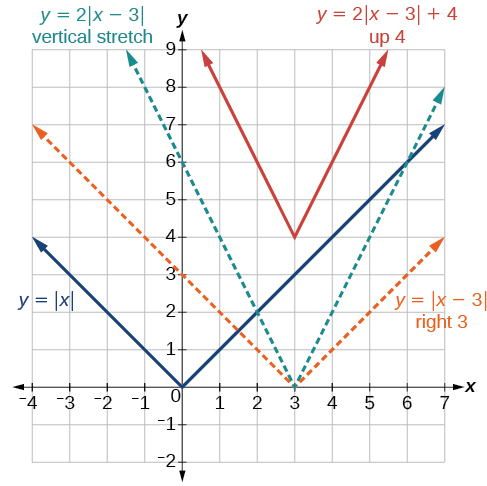
Figure 3 shows the graph of [latex]\,y=2|x–3|+4.\,[/latex] The graph of [latex]\,y=|x|\,[/latex] has been shifted right 3 units, vertically stretched by a factor of 2, and shifted up 4 units. This means that the corner point is located at [latex]\,\left(3,4\right)\,[/latex] for this transformed function.

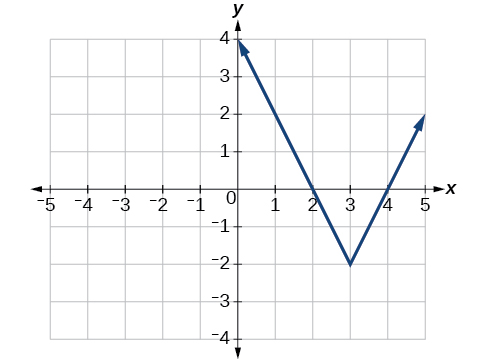
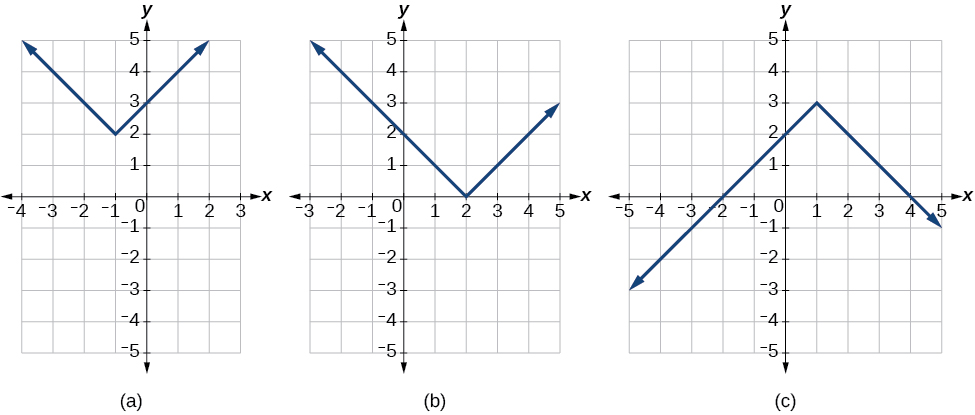
Writing an Equation for an Absolute Value Function Given a Graph

Write an equation for the function graphed in Figure 4.

The basic absolute value function changes direction at the origin, so this graph has been shifted to the right 3 units and down 2 units from the basic toolkit function. See Figure 5.

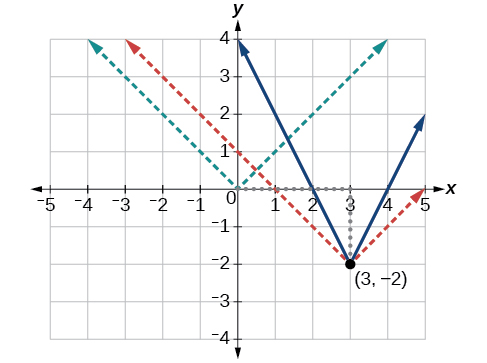
We also notice that the graph appears vertically stretched because the width of the final graph on a horizontal line is not equal to 2 times the vertical distance from the corner to this line, as it would be for an unstretched absolute value function. Instead, the width is equal to 1 times the vertical distance, as shown in Figure 6.

From this information, we can write the equation

Note that these equations are algebraically equivalent—the stretch for an absolute value function can be written interchangeably as a vertical or horizontal stretch or compression.

If we couldn’t observe the stretch of the function from the graphs, could we algebraically determine it?

Yes. If we are unable to determine the stretch based on the width of the graph, we can solve for the stretch factor by putting in a known pair of values for [latex]\,x\,[/latex] and [latex]\,f\left(x\right).[/latex]

Now substituting in the point (1, 2)

Write the equation for the absolute value function that is horizontally shifted left 2 units, vertically flipped, and vertically shifted up 3 units.

[latex]f\left(x\right)=-|x+2|+3[/latex]

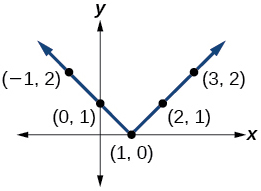
Do the graphs of absolute value functions always intersect the vertical axis? The horizontal axis?

Yes, they always intersect the vertical axis. The graph of an absolute value function will intersect the vertical axis when the input is zero.

No, they do not always intersect the horizontal axis. The graph may or may not intersect the horizontal axis, depending on how the graph has been shifted and reflected. It is possible for the absolute value function to intersect the horizontal axis at zero, one, or two points (see Figure 7).

Access these online resources for additional instruction and practice with graphing absolute value equations.

Solving an Absolute Value Equation

In Other Type of Equations , we touched on the concepts of absolute value equations. Now that we understand a little more about their graphs, we can take another look at these types of equations. Now that we can graph an absolute value function, we will learn how to solve an absolute value equation. To solve an equation such as [latex]\,8=|2x-6|,\,[/latex] we notice that the absolute value will be equal to 8 if the quantity inside the absolute value is 8 or -8. This leads to two different equations we can solve independently.

Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.

An absolute value equation is an equation in which the unknown variable appears in absolute value bars. For example,

Solutions to Absolute Value Equations

For real numbers [latex]A[/latex] and [latex]B[/latex], an equation of the form [latex]|A|=B,[/latex] with [latex]B\ge 0,[/latex] will have solutions when [latex]A=B[/latex] or [latex]A=-B.[/latex] If B<0 , the equation [latex]|A|=B[/latex] has no solution.

Given the formula for an absolute value function, find the horizontal intercepts of its graph .

• Isolate the absolute value term.
• Use [latex]\,|A|=B\,[/latex] to write [latex]\,A=B\,[/latex] or [latex]\,\mathrm{-A}=B,\,[/latex] assuming [latex]\,B>0.[/latex]
• Solve for [latex]\,x.\,[/latex]

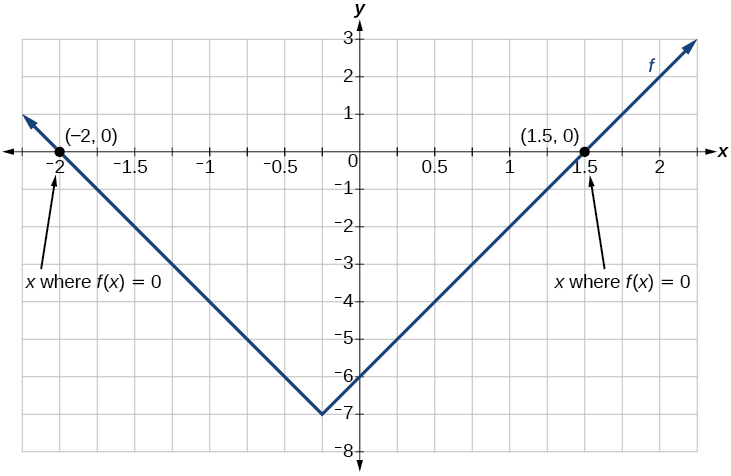
Finding the Zeros of an Absolute Value Function

For the function[latex]\,f\left(x\right)=|4x+1|-7,[/latex] find the values of[latex]\,x\,[/latex]such that[latex]\,f\left(x\right)=0.[/latex]

The function outputs 0 when[latex]\,x=\frac{3}{2}\,[/latex]or[latex]\,x=-2.[/latex] See Figure 8.

For the function [latex]\,f\left(x\right)=|2x-1|-3,[/latex] find the values of [latex]\,x\,[/latex] such that [latex]\,f\left(x\right)=0.[/latex]

[latex]x=-1\,[/latex] or [latex]\,\,x=2[/latex]

Should we always expect two answers when solving[latex]\,|A|=B?[/latex]

No. We may find one, two, or even no answers. For example, there is no solution to  [latex]\,2+|3x-5|=1.[/latex]

Key Concepts

• Applied problems, such as ranges of possible values, can also be solved using the absolute value function.
• The graph of the absolute value function resembles a letter V. It has a corner point at which the graph changes direction.
• In an absolute value equation, an unknown variable is the input of an absolute value function.
• If the absolute value of an expression is set equal to a positive number, expect two solutions for the unknown variable.

Section Exercises

• How do you solve an absolute value equation?

Isolate the absolute value term so that the equation is of the form[latex]\,|A|=B.\,[/latex]Form one equation by setting the expression inside the absolute value symbol,[latex]\,A,\,[/latex]equal to the expression on the other side of the equation,[latex]\,B.\,[/latex]Form a second equation by setting[latex]\,A\,[/latex]equal to the opposite of the expression on the other side of the equation,[latex]\,-B.\,[/latex]Solve each equation for the variable.

• How can you tell whether an absolute value function has two x -intercepts without graphing the function?
• When solving an absolute value function, the isolated absolute value term is equal to a negative number. What does that tell you about the graph of the absolute value function?

The graph of the absolute value function does not cross the[latex]\,x[/latex]-axis, so the graph is either completely above or completely below the[latex]\,x[/latex]-axis.

• How can you use the graph of an absolute value function to determine the x -values for which the function values are negative?
• Describe all numbers[latex]\,x\,[/latex]that are at a distance of[latex]\,\frac{1}{2}\,[/latex]from the number −4. Express this set of numbers using absolute value notation.

[latex]\,|x+4|=\frac{1}{2}\,[/latex]

• Describe the situation in which the distance that point[latex]\,x\,[/latex]is from 10 is at least 15 units. Express this set of numbers using absolute value notation.
• Find all function values[latex]\,f\left(x\right)\,[/latex]such that the distance from[latex]\,f\left(x\right)\,[/latex]to the value 8 is less than 0.03 units. Express this set of numbers using absolute value notation.

[latex]|f\left(x\right)-8|[/latex] <0.03

For the following exercises, find the x – and y -intercepts of the graphs of each function.

• [latex]f\left(x\right)=4|x-3|+4[/latex]
• [latex]f\left(x\right)=-3|x-2|-1[/latex]

[latex]\left(0,-7\right);\,[/latex]no[latex]\,x[/latex]-intercepts

• [latex]f\left(x\right)=-2|x+1|+6[/latex]
• [latex]f\left(x\right)=-5|x+2|+15[/latex]

[latex]\left(0,\,5\right),\left(1,0\right),\left(-5,0\right)[/latex]

• [latex]f\left(x\right)=2|x-1|-6[/latex]
• [latex]f\left(x\right)=|-2x+1|-13[/latex]

[latex]\left(0,-12\right),\left(-6,0\right),\left(7,0\right)[/latex]

• [latex]f\left(x\right)=-|x-9|+16[/latex]

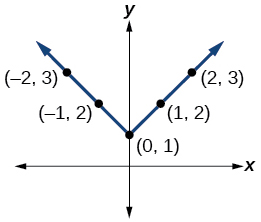
For the following exercises, graph the absolute value function. Plot at least five points by hand for each graph.

• [latex]y=|x-1|[/latex]

• [latex]y=|x+1|[/latex]
• [latex]y=|x|+1[/latex]

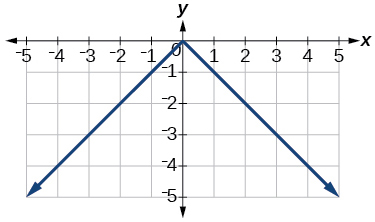
For the following exercises, graph the given functions by hand.

• [latex]y=|x|-2[/latex]
• [latex]y=-|x|[/latex]

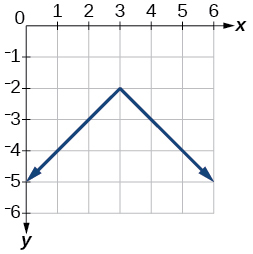
• [latex]y=-|x|-2[/latex]
• [latex]y=-|x-3|-2[/latex]

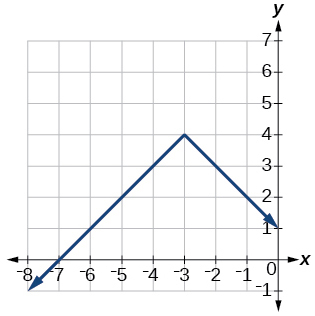
• [latex]f\left(x\right)=-|x-1|-2[/latex]
• [latex]f\left(x\right)=-|x+3|+4[/latex]

• [latex]f\left(x\right)=2|x+3|+1[/latex]
• [latex]f\left(x\right)=3|x-2|+3[/latex]

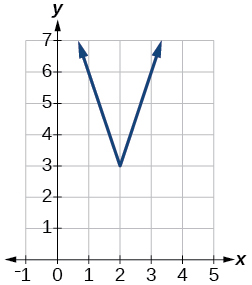
• [latex]f\left(x\right)=|2x-4|-3[/latex]
• [latex]f\left(x\right)=|3x+9|+2[/latex]

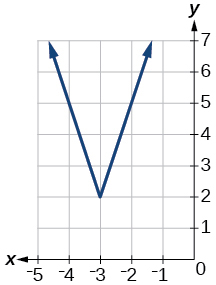
• [latex]f\left(x\right)=-|x-1|-3[/latex]
• [latex]f\left(x\right)=-|x+4|-3[/latex]

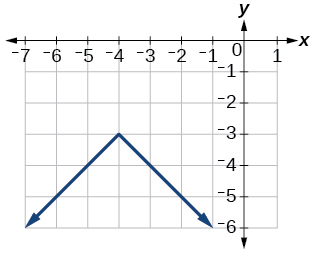
• [latex]f\left(x\right)=\frac{1}{2}|x+4|-3[/latex]
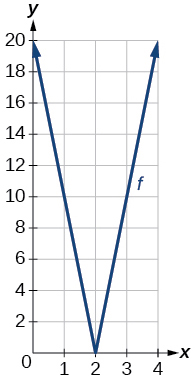
• Use a graphing utility to graph [latex]f\left(x\right)=10|x-2|[/latex] on the viewing window [latex]\left[0,4\right].[/latex] Identify the corresponding range. Show the graph.

range:[latex]\,\left[0,20\right][/latex]

• Use a graphing utility to graph[latex]\,f\left(x\right)=-100|x|+100\,[/latex]on the viewing window[latex]\,\left[-5,5\right].\,[/latex]Identify the corresponding range. Show the graph.

For the following exercises, graph each function using a graphing utility. Specify the viewing window.

• [latex]f\left(x\right)=-0.1|0.1\left(0.2-x\right)|+0.3[/latex]

[latex]x\text{-}[/latex]intercepts:

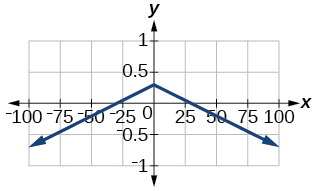
• [latex]f\left(x\right)=4×{10}^{9}|x-\left(5×{10}^{9}\right)|+2×{10}^{9}[/latex]

For the following exercises, solve the inequality.

• If possible, find all values of[latex]\,a\,[/latex]such that there are no [latex]\,y[/latex]-intercepts for[latex]\,f\left(x\right)=2|x+1|+a.[/latex]

There is no solution for[latex]\,a\,[/latex]that will keep the function from having a[latex]\,y[/latex]-intercept. The absolute value function always crosses the [latex]\,y[/latex]-intercept when[latex]\,x=0.[/latex]

• If possible, find all values of [latex]a[/latex] such that there are no [latex]x\text{-}[/latex]intercepts for [latex]f\left(x\right)=2|x+1|+a.[/latex]

Real-World Applications

• The true proportion[latex]\,p\,[/latex]of people who give a favorable rating to Congress is 8% with a margin of error of 1.5%. Describe this statement using an absolute value equation.

[latex]|p-0.08|\le 0.015[/latex]

• Students who score within 18 points of the number 82 will pass a particular test. Write this statement using absolute value notation and use the variable[latex]\,x\,[/latex]for the score.
• A machinist must produce a bearing that is within 0.01 inches of the correct diameter of 5.0 inches. Using[latex]\,x\,[/latex]as the diameter of the bearing, write this statement using absolute value notation.

[latex]|x-5.0|\le 0.01[/latex]

• The tolerance for a ball bearing is 0.01. If the true diameter of the bearing is to be 2.0 inches and the measured value of the diameter is[latex]\,x\,[/latex]inches, express the tolerance using absolute value notation.

Media Attributions

• 3.7 Figure 1 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
• 3.7 Figure 2 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
• 3.7 Figure 3 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
• 3.7 Figure 4 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
• 3.7 Figure 5 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
• 3.7 Figure 6 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
• 3.7 Figure 7 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
• 3.7 Figure 8 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
• 3.7 Solution-15 © OpenStax College Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 3.7 Solution-17 © OpenStax College Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 3.7 Solution-19 © OpenStax College Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 3.7 Solution-21 © OpenStax College Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 3.7 Solution-23 © OpenStax College Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 3.7 Solution-25 © OpenStax College Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 3.7 Solution-27 © OpenStax College Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 3.7 Solution-29 © OpenStax College Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 3.7 Solution-31 © OpenStax College Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 3.7 Solution-33 © OpenStax College Algebra and Trigonometry is licensed under a CC BY (Attribution) license

College Algebra Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.9: Absolute Value Functions

• Last updated
• Save as PDF
• Page ID 59844

• David Arnold
• College of the Redwoods
• 1.9.1: Piecewise-Defined Functions In preparation for the definition of the absolute value function, it is extremely important to have a good grasp of the concept of a piecewise-defined function.
• 1.9.2: Absolute Value The absolute value of a number is a measure of its magnitude, sans (without) its sign.
• 1.9.3: Absolute Value Equations
• 1.9.4: Absolute Value Inequalities

Thumbnail: The graph of the absolute value function for real numbers. (CC BY-SA 3.0; Qef and Ævar Arnfjörð Bjarmason via Wikipedia).

2.7 Solve Absolute Value Inequalities

Learning objectives.

• Solve absolute value equations
• Solve absolute value inequalities with “less than”
• Solve absolute value inequalities with “greater than”
• Solve applications with absolute value

Be Prepared 2.7

Before you get started, take this readiness quiz.

• Evaluate: − | 7 | . − | 7 | . If you missed this problem, review Example 1.12 .
• Fill in < , > , < , > , or = = for each of the following pairs of numbers. ⓐ | −8 | ___ − | −8 | | −8 | ___ − | −8 | ⓑ 12 ___ − | −12 | 12 ___ − | −12 | ⓒ | −6 | ___ − 6 | −6 | ___ − 6 ⓓ − ( −15 ) ___ − | −15 | − ( −15 ) ___ − | −15 | If you missed this problem, review Example 1.12 .
• Simplify: 14 − 2 | 8 − 3 ( 4 − 1 ) | . 14 − 2 | 8 − 3 ( 4 − 1 ) | . If you missed this problem, review Example 1.13 .

Solve Absolute Value Equations

As we prepare to solve absolute value equations, we review our definition of absolute value .

Absolute Value

The absolute value of a number is its distance from zero on the number line.

The absolute value of a number n is written as | n | | n | and | n | ≥ 0 | n | ≥ 0 for all numbers.

Absolute values are always greater than or equal to zero.

We learned that both a number and its opposite are the same distance from zero on the number line. Since they have the same distance from zero, they have the same absolute value. For example:

−5 −5 is 5 units away from 0, so | −5 | = 5 . | −5 | = 5 .

5 5 is 5 units away from 0, so | 5 | = 5 . | 5 | = 5 .

Figure 2.6 illustrates this idea.

For the equation | x | = 5 , | x | = 5 , we are looking for all numbers that make this a true statement. We are looking for the numbers whose distance from zero is 5. We just saw that both 5 and −5 −5 are five units from zero on the number line. They are the solutions to the equation.

The solution can be simplified to a single statement by writing x = ± 5 . x = ± 5 . This is read, “ x is equal to positive or negative 5”.

We can generalize this to the following property for absolute value equations.

Absolute Value Equations

For any algebraic expression, u , and any positive real number, a ,

Remember that an absolute value cannot be a negative number.

Example 2.68

Solve: ⓐ | x | = 8 | x | = 8 ⓑ | y | = −6 | y | = −6 ⓒ | z | = 0 | z | = 0

ⓐ | x | = 8 Write the equivalent equations. x = −8 or x = 8 x = ± 8 | x | = 8 Write the equivalent equations. x = −8 or x = 8 x = ± 8 ⓑ | y | = −6 No solution | y | = −6 No solution Since an absolute value is always positive, there are no solutions to this equation. ⓒ | z | = 0 Write the equivalent equations. z = −0 or z = 0 Since −0 = 0 , z = 0 | z | = 0 Write the equivalent equations. z = −0 or z = 0 Since −0 = 0 , z = 0 Both equations tell us that z = 0 z = 0 and so there is only one solution.

Try It 2.135

Solve: ⓐ | x | = 2 | x | = 2 ⓑ | y | = −4 | y | = −4 ⓒ | z | = 0 | z | = 0

Try It 2.136

Solve: ⓐ | x | = 11 | x | = 11 ⓑ | y | = −5 | y | = −5 ⓒ | z | = 0 | z | = 0

To solve an absolute value equation , we first isolate the absolute value expression using the same procedures we used to solve linear equations. Once we isolate the absolute value expression we rewrite it as the two equivalent equations.

Example 2.69

How to solve absolute value equations.

Solve | 5 x − 4 | − 3 = 8 . | 5 x − 4 | − 3 = 8 .

Try It 2.137

Solve: | 3 x − 5 | − 1 = 6 . | 3 x − 5 | − 1 = 6 .

Try It 2.138

Solve: | 4 x − 3 | − 5 = 2 . | 4 x − 3 | − 5 = 2 .

The steps for solving an absolute value equation are summarized here.

Solve absolute value equations.

• Step 1. Isolate the absolute value expression.
• Step 2. Write the equivalent equations.
• Step 3. Solve each equation.
• Step 4. Check each solution.

Example 2.70

Solve 2 | x − 7 | + 5 = 9 . 2 | x − 7 | + 5 = 9 .

Try It 2.139

Solve: 3 | x − 4 | − 4 = 8 . 3 | x − 4 | − 4 = 8 .

Try It 2.140

Solve: 2 | x − 5 | + 3 = 9 . 2 | x − 5 | + 3 = 9 .

Remember, an absolute value is always positive!

Example 2.71

Solve: | 2 3 x − 4 | + 11 = 3 . | 2 3 x − 4 | + 11 = 3 .

| 2 3 x − 4 | + 11 = 3 Isolate the absolute value term. | 2 3 x − 4 | = −8 An absolute value cannot be negative. No solution | 2 3 x − 4 | + 11 = 3 Isolate the absolute value term. | 2 3 x − 4 | = −8 An absolute value cannot be negative. No solution

Try It 2.141

Solve: | 3 4 x − 5 | + 9 = 4 . | 3 4 x − 5 | + 9 = 4 .

Try It 2.142

Solve: | 5 6 x + 3 | + 8 = 6 . | 5 6 x + 3 | + 8 = 6 .

Some of our absolute value equations could be of the form | u | = | v | | u | = | v | where u and v are algebraic expressions. For example, | x − 3 | = | 2 x + 1 | . | x − 3 | = | 2 x + 1 | .

How would we solve them? If two algebraic expressions are equal in absolute value, then they are either equal to each other or negatives of each other. The property for absolute value equations says that for any algebraic expression, u , and a positive real number, a , if | u | = a , | u | = a , then u = − a u = − a or u = a . u = a .

This tell us that

This leads us to the following property for equations with two absolute values.

Equations with Two Absolute Values

For any algebraic expressions, u and v ,

When we take the opposite of a quantity, we must be careful with the signs and to add parentheses where needed.

Example 2.72

Solve: | 5 x − 1 | = | 2 x + 3 | . | 5 x − 1 | = | 2 x + 3 | .

Write the equivalent equations. 5 x − 1 = − ( 2 x + 3 ) or 5 x − 1 = 2 x + 3 Solve each equation. 5 x − 1 = −2 x − 3 or 3 x − 1 = 3 7 x − 1 = −3 3 x = 4 7 x = −2 x = 4 3 x = − 2 7 or x = 4 3 Check. We leave the check to you. Write the equivalent equations. 5 x − 1 = − ( 2 x + 3 ) or 5 x − 1 = 2 x + 3 Solve each equation. 5 x − 1 = −2 x − 3 or 3 x − 1 = 3 7 x − 1 = −3 3 x = 4 7 x = −2 x = 4 3 x = − 2 7 or x = 4 3 Check. We leave the check to you.

Try It 2.143

Solve: | 7 x − 3 | = | 3 x + 7 | . | 7 x − 3 | = | 3 x + 7 | .

Try It 2.144

Solve: | 6 x − 5 | = | 3 x + 4 | . | 6 x − 5 | = | 3 x + 4 | .

Solve Absolute Value Inequalities with “Less Than”

Let’s look now at what happens when we have an absolute value inequality . Everything we’ve learned about solving inequalities still holds, but we must consider how the absolute value impacts our work.

Again we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line. For the equation | x | = 5 , | x | = 5 , we saw that both 5 and −5 −5 are five units from zero on the number line. They are the solutions to the equation.

What about the inequality | x | ≤ 5 ? | x | ≤ 5 ? Where are the numbers whose distance is less than or equal to 5? We know −5 −5 and 5 are both five units from zero. All the numbers between −5 −5 and 5 are less than five units from zero. See Figure 2.7 .

In a more general way, we can see that if | u | ≤ a , | u | ≤ a , then − a ≤ u ≤ a . − a ≤ u ≤ a . See Figure 2.8 .

This result is summarized here.

Absolute Value Inequalities with < < or ≤ ≤

After solving an inequality, it is often helpful to check some points to see if the solution makes sense. The graph of the solution divides the number line into three sections. Choose a value in each section and substitute it in the original inequality to see if it makes the inequality true or not. While this is not a complete check, it often helps verify the solution.

Example 2.73

Solve | x | < 7 . | x | < 7 . Graph the solution and write the solution in interval notation.

To verify, check a value in each section of the number line showing the solution. Choose numbers such as −8 , −8 , 1, and 9.

Try It 2.145

Graph the solution and write the solution in interval notation: | x | < 9 . | x | < 9 .

Try It 2.146

Graph the solution and write the solution in interval notation: | x | < 1 . | x | < 1 .

Example 2.74

Solve | 5 x − 6 | ≤ 4 . | 5 x − 6 | ≤ 4 . Graph the solution and write the solution in interval notation.

Try It 2.147

Solve | 2 x − 1 | ≤ 5 . | 2 x − 1 | ≤ 5 . Graph the solution and write the solution in interval notation:

Try It 2.148

Solve | 4 x − 5 | ≤ 3 . | 4 x − 5 | ≤ 3 . Graph the solution and write the solution in interval notation:

Solve absolute value inequalities with < or ≤.

• Step 2. Write the equivalent compound inequality. | u | < a is equivalent to − a < u < a | u | ≤ a is equivalent to − a ≤ u ≤ a | u | < a is equivalent to − a < u < a | u | ≤ a is equivalent to − a ≤ u ≤ a
• Step 3. Solve the compound inequality.
• Step 4. Graph the solution
• Step 5. Write the solution using interval notation.

Solve Absolute Value Inequalities with “Greater Than”

What happens for absolute value inequalities that have “greater than”? Again we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line.

We started with the inequality | x | ≤ 5 . | x | ≤ 5 . We saw that the numbers whose distance is less than or equal to five from zero on the number line were −5 −5 and 5 and all the numbers between −5 −5 and 5. See Figure 2.9 .

Now we want to look at the inequality | x | ≥ 5 . | x | ≥ 5 . Where are the numbers whose distance from zero is greater than or equal to five?

Again both −5 −5 and 5 are five units from zero and so are included in the solution. Numbers whose distance from zero is greater than five units would be less than −5 −5 and greater than 5 on the number line. See Figure 2.10 .

In a more general way, we can see that if | u | ≥ a , | u | ≥ a , then u ≤ − a u ≤ − a or u ≤ a . u ≤ a . See Figure 2.11 .

Absolute Value Inequalities with > or ≥

Example 2.75.

Solve | x | > 4 . | x | > 4 . Graph the solution and write the solution in interval notation.

To verify, check a value in each section of the number line showing the solution. Choose numbers such as −6 , −6 , 0, and 7.

Try It 2.149

Solve | x | > 2 . | x | > 2 . Graph the solution and write the solution in interval notation.

Try It 2.150

Solve | x | > 1 . | x | > 1 . Graph the solution and write the solution in interval notation.

Example 2.76

Solve | 2 x − 3 | ≥ 5 . | 2 x − 3 | ≥ 5 . Graph the solution and write the solution in interval notation.

Try It 2.151

Solve | 4 x − 3 | ≥ 5 . | 4 x − 3 | ≥ 5 . Graph the solution and write the solution in interval notation.

Try It 2.152

Solve | 3 x − 4 | ≥ 2 . | 3 x − 4 | ≥ 2 . Graph the solution and write the solution in interval notation.

Solve absolute value inequalities with > or ≥.

• Step 2. Write the equivalent compound inequality. | u | > a is equivalent to u < − a or u > a | u | ≥ a is equivalent to u ≤ − a or u ≥ a | u | > a is equivalent to u < − a or u > a | u | ≥ a is equivalent to u ≤ − a or u ≥ a

Solve Applications with Absolute Value

Absolute value inequalities are often used in the manufacturing process. An item must be made with near perfect specifications. Usually there is a certain tolerance of the difference from the specifications that is allowed. If the difference from the specifications exceeds the tolerance, the item is rejected.

Example 2.77

The ideal diameter of a rod needed for a machine is 60 mm. The actual diameter can vary from the ideal diameter by 0.075 0.075 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?

Try It 2.153

The ideal diameter of a rod needed for a machine is 80 mm. The actual diameter can vary from the ideal diameter by 0.009 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?

Try It 2.154

The ideal diameter of a rod needed for a machine is 75 mm. The actual diameter can vary from the ideal diameter by 0.05 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?

Access this online resource for additional instruction and practice with solving linear absolute value equations and inequalities.

• Solving Linear Absolute Value Equations and Inequalities

Section 2.7 Exercises

Practice makes perfect.

In the following exercises, solve.

ⓐ | x | = 6 | x | = 6 ⓑ | y | = −3 | y | = −3 ⓒ | z | = 0 | z | = 0

ⓐ | x | = 4 | x | = 4 ⓑ | y | = −5 | y | = −5 ⓒ | z | = 0 | z | = 0

ⓐ | x | = 7 | x | = 7 ⓑ | y | = −11 | y | = −11 ⓒ | z | = 0 | z | = 0

ⓐ | x | = 3 | x | = 3 ⓑ | y | = −1 | y | = −1 ⓒ | z | = 0 | z | = 0

| 2 x − 3 | − 4 = 1 | 2 x − 3 | − 4 = 1

| 4 x − 1 | − 3 = 0 | 4 x − 1 | − 3 = 0

| 3 x − 4 | + 5 = 7 | 3 x − 4 | + 5 = 7

| 4 x + 7 | + 2 = 5 | 4 x + 7 | + 2 = 5

4 | x − 1 | + 2 = 10 4 | x − 1 | + 2 = 10

3 | x − 4 | + 2 = 11 3 | x − 4 | + 2 = 11

3 | 4 x − 5 | − 4 = 11 3 | 4 x − 5 | − 4 = 11

3 | x + 2 | − 5 = 4 3 | x + 2 | − 5 = 4

−2 | x − 3 | + 8 = −4 −2 | x − 3 | + 8 = −4

−3 | x − 4 | + 4 = −5 −3 | x − 4 | + 4 = −5

| 3 4 x − 3 | + 7 = 2 | 3 4 x − 3 | + 7 = 2

| 3 5 x − 2 | + 5 = 2 | 3 5 x − 2 | + 5 = 2

| 1 2 x + 5 | + 4 = 1 | 1 2 x + 5 | + 4 = 1

| 1 4 x + 3 | + 3 = 1 | 1 4 x + 3 | + 3 = 1

| 3 x − 2 | = | 2 x − 3 | | 3 x − 2 | = | 2 x − 3 |

| 4 x + 3 | = | 2 x + 1 | | 4 x + 3 | = | 2 x + 1 |

| 6 x − 5 | = | 2 x + 3 | | 6 x − 5 | = | 2 x + 3 |

| 6 − x | = | 3 − 2 x | | 6 − x | = | 3 − 2 x |

Solve Absolute Value Inequalities with “less than”

In the following exercises, solve each inequality. Graph the solution and write the solution in interval notation.

| x | < 5 | x | < 5

| x | < 1 | x | < 1

| x | ≤ 8 | x | ≤ 8

| x | ≤ 3 | x | ≤ 3

| 3 x − 3 | ≤ 6 | 3 x − 3 | ≤ 6

| 2 x − 5 | ≤ 3 | 2 x − 5 | ≤ 3

| 2 x + 3 | + 5 < 4 | 2 x + 3 | + 5 < 4

| 3 x − 7 | + 3 < 1 | 3 x − 7 | + 3 < 1

| 4 x − 3 | < 1 | 4 x − 3 | < 1

| 6 x − 5 | < 7 | 6 x − 5 | < 7

| x − 4 | ≤ −1 | x − 4 | ≤ −1

| 5 x + 1 | ≤ −2 | 5 x + 1 | ≤ −2

Solve Absolute Value Inequalities with “greater than”

| x | > 3 | x | > 3

| x | > 6 | x | > 6

| x | ≥ 2 | x | ≥ 2

| x | ≥ 5 | x | ≥ 5

| 3 x − 8 | > − 1 | 3 x − 8 | > − 1

| x − 5 | > − 2 | x − 5 | > − 2

| 3 x − 2 | > 4 | 3 x − 2 | > 4

| 2 x − 1 | > 5 | 2 x − 1 | > 5

| x + 3 | ≥ 5 | x + 3 | ≥ 5

| x − 7 | ≥ 1 | x − 7 | ≥ 1

3 | x | + 4 ≥ 1 3 | x | + 4 ≥ 1

5 | x | + 6 ≥ 1 5 | x | + 6 ≥ 1

In the following exercises, solve. For each inequality, also graph the solution and write the solution in interval notation.

2 | x + 6 | + 4 = 8 2 | x + 6 | + 4 = 8

| 3 x − 4 | ≥ 2 | 3 x − 4 | ≥ 2

| 4 x − 3 | < 5 | 4 x − 3 | < 5

| 2 x − 5 | + 2 = 3 | 2 x − 5 | + 2 = 3

| 3 x + 1 | − 3 = 7 | 3 x + 1 | − 3 = 7

| 7 x + 2 | + 8 < 4 | 7 x + 2 | + 8 < 4

5 | 2 x − 1 | − 3 = 7 5 | 2 x − 1 | − 3 = 7

| x − 7 | > − 3 | x − 7 | > − 3

| 8 − x | = | 4 − 3 x | | 8 − x | = | 4 − 3 x |

A chicken farm ideally produces 200,000 eggs per day. But this total can vary by as much as 25,000 eggs. What is the maximum and minimum expected production at the farm?

An organic juice bottler ideally produces 215,000 bottle per day. But this total can vary by as much as 7,500 bottles. What is the maximum and minimum expected production at the bottling company?

In order to insure compliance with the law, Miguel routinely overshoots the weight of his tortillas by 0.5 gram. He just received a report that told him that he could be losing as much as $100,000 per year using this practice. He now plans to buy new equipment that guarantees the thickness of the tortilla within 0.005 inches. If the ideal thickness of the tortilla is 0.04 inches, what thickness of tortillas will be guaranteed?

At Lilly’s Bakery, the ideal weight of a loaf of bread is 24 ounces. By law, the actual weight can vary from the ideal by 1.5 ounces. What range of weight will be acceptable to the inspector without causing the bakery being fined?

Writing Exercises

Write a graphical description of the absolute value of a number.

In your own words, explain how to solve the absolute value inequality, | 3 x − 2 | ≥ 4 . | 3 x − 2 | ≥ 4 .

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra/pages/1-introduction

• Authors: Lynn Marecek
• Publisher/website: OpenStax
• Book title: Intermediate Algebra
• Publication date: Mar 14, 2017
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra/pages/2-7-solve-absolute-value-inequalities

© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.