maths coursework ideas

IB Maths IA examples

Type a search phrase to find the most relevant Maths IA examples for you

Not sure what to search for? You can always look through our example Internal Assessments below for inspiration.

All Maths IA Examples

Filter exemplars, modelling india’s population, what trajectory should the spaceship use to minimise the total amount of radiation obtained when travelling to the point exactly opposite of the star, want to get full marks for your ia allow us to review it for you 🎯, investigating the correlation between height and shooting ability in basketball., fourier transform in neuroscience: an application to electric signal analysis, how does the volume of water inside a bottle determine the frequency of the sound emitted by the bottle as more water is filled, fast track your coursework with mark schemes moderated by ib examiners. upgrade now 🚀, optimizing blood vessel branching, employing optimization to minimize amount of packaging material, what is the mathematical formula for the key of c major, modeling a chicken egg, modelling covid 19 using sir model, how can math demonstrate how people can play music by ear without ever reading sheet music, modelling the surface area of a ceramic pot, the mathematics behind singapore's student loans (19/20), exploration into modelling a population pyramid (19/20), how can we develop an accurate model to describe radioactive decay, how does club face loft affect how far the ball carries in golf, the determination of pi constant using geometry, calculus, and technology, an investigation into predicting the outcome of the 2020 new zealand election, how air pressure affects a soccer ball, a model of earth’s orbit, how to calculate the surface area and volume of a bottle through modelling, comparing the rates of change of in temperature for three water bottles, mathematical modelling of doraemon, extension of the moving ladder problem, lanchester’s combat model, investigating the interaction between sinusoidal sound waves and resultant superposition in assembling harmonious guitar chords, exploring an alternative method of calculating the volume of a star, investigation of the relationship between leg length and lateral jumping distance, the role of mathematics in cryptography, tower of hanoi, analysing the cost of filling and crown's structure for humans., an investigation on authorship, small neural networks for simple binary classification., modeling the curve of a dolphin kick of a swimmer, what is the relationship between gdp per capita and co2 emissions per capita, logarithmic transformations of graphs and its importance in real life, plotting log graphs of planetary patterns, bayes’ thorem and the probability of inaccurate diagnosis in 40-89 year-old individuals in relation to the excess healthcare burden of osteoporosis in the united kingdom, modelling financial market with chaos theory (received mark: 15/20).

50 IB Maths IA Topic Ideas

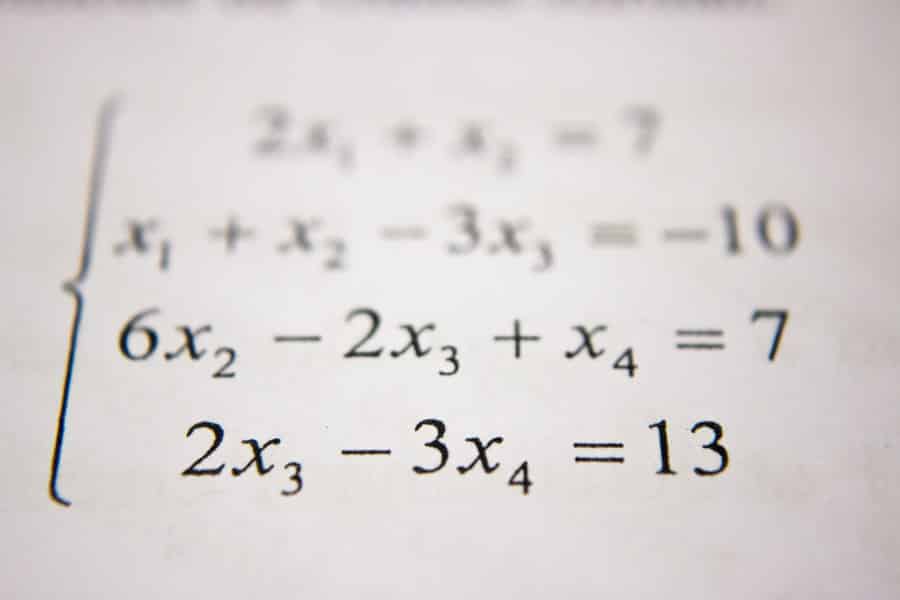
IB Maths is a struggle for most people going through their diploma. To make matters worse, on top of just doing the dreaded maths exam, we’re also expected to write a Maths IA exploration into a topic of our choice! Where do you even begin such a task? How do you even choose a topic? To make things easier, we have plenty of free Maths resources! Firstly though, we’ve compiled 50 common Maths IA topics that may spark some creative juices and set you on your way to conquering one of the hardest assignments of the diploma!

Once you have chosen your topic, you may want to check out our other posts on how to structure and format your Maths IA or how to write your IA .

NOTE: These topics are purely meant as inspiration and are not to be chosen blindly. Even though many of these topics led to high scores for some of our graduates in the past, it is important that you listen to the advice of your subject teacher before choosing any topic!

• Pascal’s triangle : Discovering patterns within this famous array of numbers
• Pythagorean triples : Can you find patterns in what numbers form a pythagorean triple?
• Monty Hall problem : How does Bayesian probability work in this real-life example, and can you add a layer of complexity to it?
• The Chinese Remainder Theorem : An insight into the mathematics of number theory
• Sum of all positive integers is -1/12? Explore this fascinating physics phenomenon through the world of sequences and series
• Birthday paradox : Why is it that in a room of people probability dictates that people are very likely to share a birthday? 
• Harmonic series : Explore why certain notes/chords in music sound dissonant, and others consonant, by looking at the ratios of frequencies between the notes.
• Optimizing areas : Optimizing the area of a rectangle is easy, but can you find a way to do it for any polygon?
• Optimizing volumes : Explore the mathematics of finding a maximum volume of a cuboid subject to some constraint
• Flow of traffic : How does mathematics feed into our traffic jams that we endure every morning?
• Football statistics : Does spending a lot of cash during the transfer window translate to more points the following year? Or is there a better predictor of a team’s success like wages, historic performance, or player valuation?
• Football statistics #2 : How does a manager sacking affect results? 
• Gini coefficient : Can you use integration to derive the gini coefficient for a few countries, allowing you to accurately compare their levels of economic inequality?
• Linear regressions : Run linear regressions using OLS to predict and estimate the effect of one variable on another.
• The Prisoner’s Dilemma : Use game theory in order to deduce the optimal strategy in this famous situation
• Tic Tac Toe : What is the optimal strategy in this legendary game? Will my probability of winning drastically increase by some move that I can make?
• Monopoly : Is there a strategy that dominates all others? Which properties should I be most excited to land on?
• Rock Paper Scissors : If I played and won with rock already, should I make sure to change what I play this time? Or is it better to switch? 
• The Toast problem : If there is a room of some number of people, how many toasts are necessary for everyone to have toasted with everyone?
• Cracking a Password : How long would it take to be able to correctly guess a password? How much safer does a password get by adding symbols or numbers?
• Stacking Balls : Suppose you want to place balls in a cardboard box, what is the optimal way to do this to use your space most effectively?
• The Wobbly Table : Many tables are wobbly because of uneven ground, but is there a way to orient the tables to make sure they are always stable?
• The Stable Marriage Problem : Is there a matching algorithm that ensures each person in society ends up with their one true love? What is the next best alternative if this is not viable?
• Mathematical Card Tricks : Look at the probabilities at play in the famous 3 card monte scam. 
• Modelling the Spread of a Virus : How long would it take for us all to be wiped out if a deadly influenza spreads throughout the population?
• The Tragedy of the Common s : Our population of fish is dwindling, but how much do we need to reduce our production by in order to ensure the fish can replenish faster than we kill?
• The Risk of Insurance : An investigation into asymmetric information and how being unsure about the future state of the world may lead us to be risk-averse
• Gabriel’s Horn : This figure has an infinite surface area but a finite volume, can you p rove this?
• Modelling the Shape of an Egg : Although it may sound easy, finding the surface area or volume of this common shape requires some in-depth mathematical investigation
• Voting Systems : What voting system ensures that the largest amount of people get the official that they would prefer? With 2 candidates this is logical, but what if they have more than 2?
• Probability : Are Oxford and Cambridge biased against state-school applicants?
• Statistics : With Tokyo 2020 around the corner, how aboutmodelling change in record performances for a particular discipline?
• Analysing Data : In the 200 meter dash, is there an advantage to a particular lane in track? 
• Coverage : Calculation of rate of deforestation, and afforestation. How long will our forests last?
• Friendly numbers, Solitary numbers, perfect numbers : Investigate what changes the condition of numbers
• Force : Calculating the intensity of a climber’s fall based upon their distance above where they last clamped in
• Königsberg bridge problem : Using networks to solve problems. 
• Handshake problem : How many handshakes are required so that everyone shakes hands with all the other people in the room? 
• The mathematics of deceit : How con artists use pyramid schemes to get rich quick!
• Modelling radioactive decay : The maths of Chernobyl – when will it be safe to live there?
• Mathematics and photography : Exploring the relationship between the aperture of a camera and a geometric sequence
• Normal Distribution : Using distributions to examine the 2008 financial crisis
• Mechanics : Body Proportions for Track and Field events
• Modelling : How does a cup of Tea cool?
• Relationships : Do BMI ratings and country wealth share a significant relationship?
• Modelling : Can we mathematically model musical chords and concepts like dissonance?
• Evaluating limits : Exploring L’Hôpital’s rule
• Chinese postman problem : How do we calculate shortest possible routes?
• Maths and Time : Exploring ideas regarding time dilation
• Plotting Planets : Using log functions to track planets!

So there we have it: 50 IB Maths IA topic ideas to give you a head-start for attacking this piece of IB coursework ! We also have similar ideas for Biology , Chemistry , Economics , History , Physics , TOK … and many many more tips and tricks on securing those top marks on our free resources page – just click the ‘Maths resources’ button!

Still feeling confused, or want some personalised help? We offer online private tuition from experienced IB graduates who got top marks in their Maths IA. 

Share article links

Related Articles

• Most Popular

30 IB Biology IA Topic Ideas!

Are you struggling with choosing your topic for your IB Biology IA? Don’t worry, we’ve all been there. Finding a topic is one of the – if not THE – most important part of writing your IA, so we want to make sure that you get it right! Luckily, there are so many great topics […]

20 IB Physics IA Topic Ideas!

Choosing where to start with an IA can be the hardest part, and this is definitely true for the Physics IA. We know that our topic has to be somewhat related to the syllabus, but where should we focus? Thankfully, we’ve asked some of our favourite IB graduates for some of the ideas they pursued! […]

25 History IA Topic Ideas!

Are you about to start your History internal assessment? We know the struggle. One of the most difficult parts about the task is finding a good History IA topic because it feels like you can just write about anything. The IB breaks it down into 7 main different types of topics that you can choose, […]

IB Maths IA: 60 Examples and Guidance

Charles Whitehouse

The International Baccalaureate Diploma Programme offers a variety of assessments for students, including Internal Assessments (IAs), which are pieces of coursework marked by students’ teachers. The Mathematics Internal Assessment follows the same assessment criteria across Mathematics Analysis and Approaches (AA) and Mathematics Application and Interpretation (AI). It forms 20% of a student’s Mathematics grade.

The International Baccalaureate (IB) made several changes to the curriculum and assessment methods, particularly in Mathematics. As of 2024, the IB has updated the syllabi for Mathematics Analysis and Approaches (AA) and Mathematics Applications and Interpretation (AI). The IAs now include a greater emphasis on real-world applications and data analysis.

In this article, we will cover everything you need to know about the IB Mathematics IA, including the structure, assessment criteria, and some tips for success.

What is the Mathematics IA?

The Maths IA is an individual exploration of an area of mathematics, based on the student’s own work with guidance from their teacher. Mathematical communication is an important part of the IA, which should be demonstrated through both effective written communication and use of formulae, diagrams, tables, and graphs. A top-rated Singapore IB tutor recommended that the exploration should be 10 to 15 pages long and students will spend 8 to 12 hours on the work.

Even A-Level Maths tutors and A-Level Further Maths tutors have found the concept of an IA-like component in IB Maths to be both challenging and rewarding, enriching the learning experience.

To learn more about the IB Maths Internal Assessment, you can have a look at the IB Maths AA resources as well as the IB Maths AI resources :

• IB Maths AA Past Papers
• IB Maths AI Past Papers

📈Boost your grades with our revision platform, used by 100,000+ students! 📝Access thousands of practice questions, study notes, and past papers for every subject. 📚 View IB Resources 📚 View A-Level Resources 📚 View GCSE Resources 📚 View IGCSE Resources

What are the assessment criteria?

Like most IB IAs, the IB Maths IA is marked on a group of 5 criteria which add up to 20 marks. Online Maths tutors recommend to look through these carefully before and during your investigation, to ensure that you are hitting the criteria to maximise your mark.

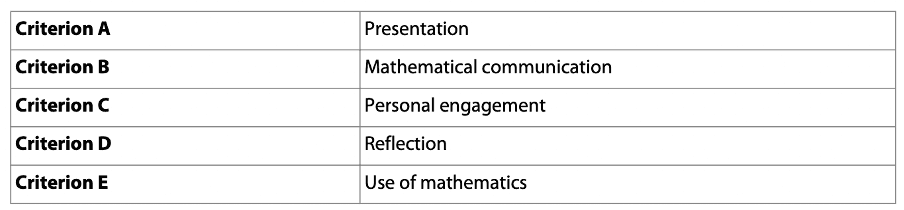
Source : IB Mathematics Applications and Interpretation Guide

Criterion A: Communication (4 marks) – This refers to the organisation and coherence of your work, and the clarity of your explanations. The investigation should be coherent, well-organized, and concise.

Criterion B: Mathematical Presentation (4 marks) – This refers to how well you use mathematical language, including notation, symbols and terminology. Your notation should be accurate, sophisticated, and consistent. Define your key terms and present your data in a varied but proper way (including labelling those graphs).

Criterion C: Personal Engagement (3 marks) – There should be evidence of outstanding personal engagement in the IA. This is primarily demonstrated through showing unique thinking, not just repeating analysis found in textbooks. This can be evidenced through analysing independently or creatively, presenting mathematical ideas in their own way, exploring the topic from different perspectives, making and testing predictions.

Criterion D: Reflection (3 marks) – This refers to how you evaluate both your sources and the strengths and weaknesses of any methodology you use. There should be “substantial evidence of critical reflection”. This could be demonstrated by considering what another stage of investigation could be, discussing implications of results, discussing strengths and weaknesses of approaches, and considering different perspectives.

Criterion E: Use of Mathematics (6 marks ) –

Note that only 6 marks are available for the actual use of mathematics! The focus of the investigation is on explaining well and analysing with genuine, personal curiosity. The level of mathematics expected also depends on the level the subject is studied at: Standard Level students’ maths is expected to be “correct”, while Higher Level students’ maths is expected to be “precise” and demonstrate “sophistication and rigour”. Use of Mathematics has been updated to emphasize the importance of not only correctness but also the innovative application of mathematical concepts.

Examiners are primarily looking for thorough understanding, which also requires clear communication of the principles behind the mathematics used - not just coming to the right answer.

Have a look at our comprehensive set resources for IB Maths developed by expert IB teachers and examiners!

- IB Maths AI SL Study Notes

- IB Maths AI HL Study Notes

- IB Maths AA SL Study Notes

- IB Maths AA HL Study Notes

What are some example research questions?

Students should choose a research area that they are interested in and have a comprehensive understanding of. Often, student may choose to consult with an expert IB Maths tutor to help them decide a good question. It should have a link to something of personal interest, as indicated by Criterion C. Popular topics include Calculus, Algebra and Number (proof), Geometry, Statistics, and Probability, or Physics. Some students make links between Math and other subjects – a good way to combine knowledge from your other IB courses!

Here are examples with details of potential research questions that could inspire your Mathematics IA:

1 - Investigating the properties of fractals and their relationship to chaos theory.

Use computer software or mathematical equations to generate and analyze fractals. Explore the patterns and properties of the fractals, such as self-similarity and complexity. Investigate how changes in the initial conditions or parameters affect the resulting fractals. Analyze the relationship between fractals and chaos theory, and how fractals can be used to model chaotic systems. Present findings through visual representations and data analysis.

2 - Analyzing the behavior of recursive sequences and their applications in computer science and cryptography.

Use mathematical formulas to generate recursive sequences and analyze their behavior. This could involve plotting the sequences and observing patterns, finding closed-form expressions for the sequences, and exploring their applications in computer science and cryptography. For example, recursive sequences can be used in algorithms for sorting and searching data, and in encryption methods such as the Fibonacci cipher. The results of the analysis could be presented in a research paper or presentation.

3 - Exploring the properties of different types of differential equations and their applications in physics and engineering.

Conduct research on the different types of differential equations and their applications in physics and engineering. This could involve studying examples of differential equations used in fields such as fluid dynamics, electromagnetism, and quantum mechanics. The properties of each type of differential equation could be analyzed, such as their order, linearity, and homogeneity. The applications of each type of differential equation could also be explored, such as how they are used to model physical systems and solve engineering problems. The findings could be presented in a report or presentation.

4 - Investigating the properties of chaotic dynamical systems and their applications in physics and biology.

Use computer simulations to model chaotic dynamical systems and explore their behavior. This could involve studying the Lorenz attractor, the logistic map, or other well-known examples of chaotic systems. The simulations could be used to investigate the sensitivity of the systems to initial conditions, the presence of strange attractors, and other key features of chaotic dynamics. The results could then be applied to real-world systems in physics and biology, such as weather patterns, population dynamics, or chemical reactions.

5 - Designing an optimized route for a delivery service to minimize travel time and fuel costs.

Use a computer program or algorithm to analyze data on the locations of delivery destinations and the most efficient routes to reach them. The program would need to take into account factors such as traffic patterns, road conditions, and the size and weight of the packages being delivered. The output would be a map or list of optimized delivery routes that minimize travel time and fuel costs. This could be used to improve the efficiency and profitability of the delivery service.

6 - Developing a model to predict the spread of infectious diseases in a population.

Collect data on the population size, infection rate, and transmission rate of the disease in question. Use this data to create a mathematical model that simulates the spread of the disease over time. The model should take into account factors such as population density, age distribution, and vaccination rates. The accuracy of the model can be tested by comparing its predictions to real-world data on the spread of the disease. The model can be used to explore different scenarios, such as the impact of different vaccination strategies or the effectiveness of quarantine measures.

7 - Investigating the relationship between different geometric shapes and their properties.

Conduct a series of experiments in which different geometric shapes are tested for various properties such as volume, surface area, and weight. The data collected could then be analyzed to determine if there is a relationship between the shape of an object and its properties. This could involve creating 3D models of the shapes using computer software, or physically measuring the shapes using laboratory equipment. The results could be presented in a graph or chart to illustrate any trends or patterns that emerge.

8 - Analyzing the behavior of projectile motion and its applications in physics.

Conduct experiments in which a projectile is launched at different angles and velocities, and its trajectory is tracked using high-speed cameras or other measurement devices. The data collected can be used to analyze the motion of the projectile and determine its velocity, acceleration, and other physical properties. This information can then be applied to real-world scenarios, such as designing rockets or calculating the trajectory of a ball in sports. Additionally, the behavior of projectile motion can be studied in different environments, such as in the presence of air resistance or in a vacuum, to better understand its applications in physics.

9 - Developing a model to predict the path of a planet based on gravitational forces.

Collect data on the mass, position, and velocity of the planet at a given time. Use the law of gravitation to calculate the gravitational forces acting on the planet from other celestial bodies in the system. Use this information to predict the path of the planet over time, taking into account any changes in velocity or direction caused by gravitational forces. The accuracy of the model could be tested by comparing its predictions to observations of the planet's actual path.

10 - Investigating the properties of conic sections and their applications in geometry and physics.

Use mathematical equations to explore the properties of conic sections such as circles, ellipses, parabolas, and hyperbolas. Investigate their applications in geometry, such as in the construction of satellite dishes and reflectors, and in physics, such as in the orbits of planets and comets. Develop models and simulations to demonstrate these applications and their impact on real-world scenarios.

Get expert help with IB Maths

The world's leading online IB Maths tutoring provider trusted by students, parents, and schools globally.

4.93 /5 based on 509 reviews

11 - Modeling the spread of a virus through a population and analyzing the effectiveness of different intervention strategies.

Develop a mathematical model that simulates the spread of the virus through a population. The model would need to take into account factors such as the infectiousness of the virus, the rate of transmission between individuals, and the effectiveness of different intervention strategies such as social distancing or vaccination. The model could then be used to analyze the effectiveness of different intervention strategies and predict the potential impact of future outbreaks. The output of the model would be a set of data and visualizations that show the predicted spread of the virus and the effectiveness of different intervention strategies.

12 - Modeling the spread of a rumor or disease through a network and analyzing the impact of network topology.

Develop a mathematical model that simulates the spread of the rumor or disease through a network. The model should take into account factors such as the probability of transmission between individuals, the rate of recovery or decay of the rumor or disease, and the structure of the network. The impact of network topology could be analyzed by comparing the spread of the rumor or disease in different types of networks, such as random, scale-free, or small-world networks. The results of the simulation could be visualized using graphs or heat maps to show the spread of the rumor or disease over time.

13 - Developing a model to predict the growth of a population over time.

Collect data on the current population size and growth rate of the population over a period of time. Use this data to develop a mathematical model that predicts the population growth rate over time. The model could be tested by comparing its predictions to actual population growth data from previous years. The model could also be used to predict future population growth and to identify factors that may affect the population's growth rate.

14 - Investigating the properties of exponential functions and their applications in finance and economics.

Develop a mathematical model for an exponential function, including its domain and range, growth/decay rate, and asymptotes. Use this model to analyze real-world scenarios in finance and economics, such as compound interest, population growth, or stock market trends. Graph the function and interpret the results in terms of the original problem.

15 - Developing a model to predict the outcomes of a sporting event based on historical data and team statistics.

Collect historical data on the two teams playing in the sporting event, including their win-loss records, player statistics, and any relevant trends or patterns. Use this data to develop a statistical model that predicts the outcome of the game based on these factors. The model can then be tested and refined using additional data and feedback from experts in the field. The final output would be a prediction of the outcome of the game, along with a measure of the model's accuracy and any potential limitations or uncertainties.

16 - Analyzing the behavior of different types of sequences and their convergence or divergence.

Use mathematical models and computer simulations to analyze the behavior of different types of sequences. This would involve testing various sequences for convergence or divergence, and comparing their behavior under different conditions. The results of these simulations could be used to develop new mathematical theories and algorithms for analyzing sequences, and could have applications in fields such as computer science, physics, and engineering.

17 -Investigating the properties of different types of angles and their relationship to geometry and trigonometry.

Conduct a study of different types of angles, including acute, obtuse, right, and straight angles. Explore their properties, such as their degree measurements, relationships to other angles, and their use in geometry and trigonometry. This could involve creating visual aids, such as diagrams or graphs, to illustrate the concepts being studied. The results of the study could be presented in a report or presentation format, highlighting the key findings and insights gained from the investigation.

18 - Developing a model to predict the outcomes of a game based on probability theory.

Collect data on the outcomes of previous games, including the teams playing, the score, and any relevant factors such as weather conditions or injuries. Use this data to calculate the probability of each team winning based on various factors. Develop a model that takes into account these probabilities and predicts the outcome of future games. The model would need to be tested and refined using additional data and statistical analysis. The final output would be a reliable model for predicting the outcomes of games based on probability theory.

19 - Analyzing the behavior of different types of inequalities and their applications in algebra and calculus.

Create a graph to visually represent the behavior of different types of inequalities, such as linear, quadratic, and exponential inequalities. Use examples to demonstrate how these inequalities can be applied in algebra and calculus, such as finding the maximum or minimum value of a function subject to certain constraints. Additionally, provide real-world applications of these concepts, such as optimizing production processes or predicting population growth.

20 - Investigating the properties of different types of graphs and their applications in computer science and social science.

Conduct a literature review to identify the different types of graphs and their applications in computer science and social science. Develop a set of criteria for evaluating the effectiveness of different types of graphs in conveying information and insights. Use these criteria to analyze and compare several examples of graphs from each field. Based on the analysis, identify the most effective types of graphs for different types of data and research questions in each field. Develop guidelines for selecting and creating effective graphs in computer science and social science research.

21 - Analyzing the behavior of different types of matrices and their applications in linear algebra and quantum mechanics.

Conduct experiments to test the behavior of different types of matrices in linear algebra and quantum mechanics. For example, in linear algebra, the inverse of a matrix can be calculated and used to solve systems of linear equations. In quantum mechanics, matrices are used to represent quantum states and operators. The behavior of these matrices can be analyzed by performing matrix operations and observing the resulting changes in the system. The applications of these matrices in various fields can also be explored and analyzed.

22 - Developing a model to predict the outcomes of a business investment based on market trends and financial data.

Collect and analyze market trends and financial data relevant to the business investment. This could include factors such as industry growth rates, consumer demand, and financial statements of similar companies. Using this data, develop a predictive model that takes into account various variables and their potential impact on the investment. The model could be tested and refined using historical data and adjusted as new information becomes available. The output would be a prediction of the potential outcomes of the investment based on the model's calculations.

23 - Modeling the spread of a forest fire and analyzing the effectiveness of different containment strategies.

Develop a computer model of the forest fire spread using data on wind direction, temperature, humidity, and fuel load. The model could be calibrated using historical data on past forest fires to ensure its accuracy. Different containment strategies could then be simulated in the model, such as creating fire breaks or using water or fire retardant chemicals to slow the spread of the fire. The effectiveness of each strategy could be evaluated by comparing the simulated fire spread with and without the strategy in place.

24 - Analyzing the behavior of different types of optimization problems and their applications in engineering and computer science.

Conduct a literature review to identify different types of optimization problems and their applications in engineering and computer science. Develop a framework for analyzing the behavior of these problems, taking into account factors such as the size of the problem, the complexity of the solution space, and the type of optimization algorithm used. Apply this framework to a set of case studies, comparing the performance of different optimization algorithms and identifying best practices for solving different types of optimization problems.

25 - Investigating the properties of different types of geometric transformations and their applications in computer graphics and animation.

Conduct a literature review to gather information on the properties of different geometric transformations and their applications in computer graphics and animation. This could include translations, rotations, scaling, and shearing. Develop a set of test cases to demonstrate the use of these transformations in creating different types of graphics and animations. The results of these tests could be used to compare the effectiveness of different types of transformations for different applications. Additionally, the limitations and challenges associated with each transformation could be identified and discussed.

26 - Developing a model to predict the outcomes of an election based on polling data.

Collect polling data from a representative sample of the population and analyze it using statistical methods such as regression analysis or machine learning algorithms. The model would need to be trained on historical election data to ensure its accuracy. The output of the model would be a prediction of the likely outcome of the election based on the polling data and the historical trends. The model could also be used to identify key factors that are driving voter behavior and to test different scenarios, such as changes in voter turnout or shifts in public opinion.

27 - Analyzing the behavior of different types of integrals and their applications in calculus and physics.

Conduct a series of experiments to analyze the behavior of different types of integrals, such as definite and indefinite integrals, and their applications in calculus and physics. For example, one experiment could involve calculating the area under a curve using both definite and indefinite integrals and comparing the results. Another experiment could involve analyzing the motion of an object using calculus and determining its velocity and acceleration at different points in time. The results of these experiments could be used to develop a deeper understanding of the behavior of integrals and their applications in various fields.

28 - Studying the properties of different types of probability distributions and their applications in statistics and finance.

Conduct a literature review to gather information on different types of probability distributions and their applications in statistics and finance. Develop a theoretical framework to analyze the properties of these distributions and their relevance in different contexts. Use statistical software to simulate data and test the theoretical framework. Analyze the results and draw conclusions about the usefulness of different probability distributions in various applications.

29 - Developing a model to predict the outcomes of a marketing campaign based on consumer data.

Collect consumer data such as demographics, purchasing habits, and social media activity. Use this data to identify patterns and trends that can be used to develop a predictive model. The model would need to be trained using historical data on marketing campaigns and their outcomes. Once the model is trained, it can be used to predict the outcomes of future marketing campaigns based on the input data. The accuracy of the model can be tested by comparing its predictions to the actual outcomes of the campaigns.

30 - Investigating the properties of different types of symmetry and their relationship to geometry and physics.

Conduct a study of different types of symmetry, such as bilateral, radial, and rotational symmetry. This could involve creating models or diagrams of different symmetrical shapes and analyzing their properties, such as the number of axes of symmetry and the angles of rotation. The relationship between symmetry and geometry could be explored by examining how different symmetrical shapes can be used to create geometric patterns. The relationship between symmetry and physics could be investigated by exploring how symmetrical structures are used in physics, such as in the design of crystals or the study of particle physics.

31 - Modeling the spread of a rumor or news story through a population and analyzing its impact.

Develop a mathematical model that simulates the spread of the rumor or news story through a population. This model could take into account factors such as the initial number of people who hear the rumor, the rate at which they share it with others, and the likelihood that each person will believe and share the rumor. The impact of the rumor could be analyzed by looking at factors such as changes in people's behavior or attitudes, or the spread of related rumors or misinformation. The model could be refined and tested using data from real-world examples of rumor or news story propagation.

32 - Analyzing the behavior of different types of exponential growth and decay functions and their applications in science and engineering.

Use mathematical models to analyze the behavior of exponential growth and decay functions. This could involve studying the equations that describe these functions, graphing them to visualize their behavior, and analyzing how they are used in various fields such as biology, economics, and physics. Applications could include modeling population growth, decay of radioactive materials, and the spread of diseases. The results of this analysis could be used to inform decision-making in these fields and to develop more accurate models for predicting future trends.

33 - Modeling the spread of a pandemic through a population and analyzing the effectiveness of different intervention strategies.

Develop a mathematical model that simulates the spread of the pandemic through a population, taking into account factors such as the transmission rate, incubation period, and recovery rate. The model could be used to predict the number of cases over time and the effectiveness of different intervention strategies, such as social distancing, mask-wearing, and vaccination. The model would need to be validated using real-world data and adjusted as new information becomes available. The results of the analysis could be used to inform public health policies and interventions to control the spread of the pandemic.

34 - Analyzing the behavior of different types of functions and their applications in science and engineering.

Conduct a study of different types of functions, such as linear, quadratic, exponential, and logarithmic functions, and their applications in science and engineering. This could involve analyzing real-world data sets and modeling them using different types of functions to determine which function best fits the data. The study could also explore the use of functions in fields such as physics, chemistry, and economics, and how they are used to make predictions and solve problems. The results of the study could be presented in a report or presentation, highlighting the importance of understanding the behavior of different types of functions in various fields.

35 - Analyzing the behavior of different types of numerical methods for solving differential equations and their applications in science and engineering.

Conduct a series of simulations using different numerical methods for solving differential equations, such as Euler's method, Runge-Kutta methods, and finite difference methods. The simulations could involve modeling physical phenomena such as fluid flow, heat transfer, or chemical reactions. The accuracy and efficiency of each method could be compared by analyzing the error and computational time for each simulation. The results could be applied to optimize numerical methods for solving differential equations in various scientific and engineering applications.

36 - Developing a model to predict the outcomes of a medical treatment based on patient data and medical history.

Collect patient data and medical history, including demographic information, medical conditions, medications, and treatment outcomes. Use statistical analysis and machine learning algorithms to develop a predictive model that can accurately predict the outcomes of a medical treatment based on patient data and medical history. The model would need to be validated using a separate set of patient data to ensure its accuracy and reliability. The model could then be used to inform medical decision-making and improve patient outcomes.

37 - Analyzing the behavior of different types of linear regression models and their applications in analyzing trends in public opinion polls.

Collect data from public opinion polls on a particular topic of interest, such as political preferences or social attitudes. Use different types of linear regression models, such as simple linear regression, multiple linear regression, and logistic regression, to analyze the data and identify trends and patterns. Compare the performance of the different models and determine which one is most appropriate for the specific data set and research question. The results of the analysis could be used to make predictions or inform policy decisions.

38 - Developing a model to predict the growth of a startup company based on market trends and financial data.

Collect market trend data and financial data for a range of startup companies. Use statistical analysis to identify patterns and correlations between the data. Develop a predictive model based on these patterns and correlations, taking into account factors such as industry trends, competition, funding, and management. The model could be tested and refined using data from existing startups, and could be used to make predictions about the growth potential of new startups based on their characteristics and market conditions.

39 - Studying the properties of different types of statistical distributions and their applications in analyzing public health data.

Analyze public health data using different statistical distributions such as normal, Poisson, and binomial distributions. This would involve understanding the properties and characteristics of each distribution and selecting the appropriate one based on the nature of the data being analyzed. The data could then be plotted and analyzed using statistical software to identify trends and patterns, and to draw conclusions about the health outcomes being studied. The results could be presented in the form of graphs, tables, and statistical summaries.

40 - Investigating the properties of different types of series and their convergence or divergence.

Conduct a series of tests on different types of series, such as geometric, arithmetic, and harmonic series. Use mathematical formulas and calculations to determine their convergence or divergence. Graphs and charts could be used to visually represent the data and make comparisons between the different types of series. The results of the tests could be analyzed to draw conclusions about the properties of each type of series and their behavior under different conditions.

41 - Analyzing the behavior of different types of functions and their limits.

Graph the different types of functions and analyze their behavior as the input values approach certain limits. This could involve finding the asymptotes, determining if the function is continuous or discontinuous at certain points, and identifying any points of inflection. The results could be presented in a report or presentation, highlighting the similarities and differences between the different types of functions and their limits.

42 - Investigating the properties of different types of sets and their relationships in set theory.

Conduct a comparative analysis of different types of sets, such as finite and infinite sets, empty sets, and subsets. Investigate their properties, such as cardinality, intersection, union, and complement. Use diagrams and examples to illustrate the relationships between the different types of sets. This analysis could be used to develop a deeper understanding of set theory and its applications in various fields.

43 - Exploring the properties of different types of number systems, such as real, complex, or p-adic numbers.

Conduct a literature review of the properties of different number systems and compile a list of key characteristics and equations. Then, design a series of mathematical problems that test these properties for each type of number system. These problems could include solving equations, graphing functions, and analyzing patterns. The results of these problems could be used to compare and contrast the properties of each number system.

44 - Developing a model to predict the behavior of a physical system using calculus of variations.

Collect data on the physical system being studied, such as its initial state and any external factors that may affect its behavior. Use the calculus of variations to develop a mathematical model that predicts the system's behavior over time. The model can then be tested against real-world observations to determine its accuracy and refine the model as needed. The final output would be a reliable model that accurately predicts the behavior of the physical system.

45 - Investigating the properties of different types of topological spaces and their relationships in topology.

Conduct a study of the different types of topological spaces, including Euclidean spaces, metric spaces, and topological manifolds. Analyze their properties, such as compactness, connectedness, and continuity, and explore how they are related to each other. This could involve creating visual representations of the spaces, such as diagrams or models, and using mathematical tools to analyze their properties. The results of the study could be used to better understand the fundamental principles of topology and their applications in various fields.

46 - Analyzing the behavior of different types of integrals, such as line integrals or surface integrals, and their applications in physics and engineering.

Conduct a literature review on the different types of integrals and their applications in physics and engineering. This could include researching the use of line integrals in calculating work done by a force field or the use of surface integrals in calculating flux through a surface. Based on the findings, develop a research question or hypothesis related to the behavior of a specific type of integral and its application in a particular field. Design and conduct an experiment or simulation to test the hypothesis and analyze the results to draw conclusions about the behavior of the integral and its practical applications.

47 - Developing a model to predict the behavior of a chemical reaction using chemical kinetics.

Collect data on the initial concentrations of reactants, temperature, and other relevant factors for the chemical reaction being studied. Use this data to develop a mathematical model that predicts the behavior of the reaction over time. The model could be tested by comparing its predictions to actual experimental data collected during the reaction. Adjustments could be made to the model as needed to improve its accuracy. The final model could be used to predict the behavior of the reaction under different conditions or to optimize reaction conditions for maximum efficiency.

48 - Investigating the properties of different types of algebraic structures, such as groups, rings, or fields.

Conduct a thorough literature review to gather information on the properties of different algebraic structures. Develop a clear research question or hypothesis to guide the investigation. Choose a specific algebraic structure to focus on and collect data by performing calculations and analyzing examples. Compare and contrast the properties of the chosen algebraic structure with other types of algebraic structures to draw conclusions about their similarities and differences. Present findings in a clear and organized manner, using appropriate mathematical language and notation.

49 - Analyzing the behavior of different types of functions, such as trigonometric, logarithmic, or hyperbolic functions, and their applications in science and engineering.

Conduct a study of the behavior of different types of functions, such as trigonometric, logarithmic, or hyperbolic functions, and their applications in science and engineering. This study could involve analyzing real-world data sets and identifying which type of function best fits the data. The study could also involve creating models using different types of functions to predict future outcomes or behavior. The results of this study could be used to inform decision-making in fields such as engineering, finance, or physics.

50 - Developing a model to predict the behavior of a financial market using mathematical finance.

Collect data on the financial market, such as stock prices, interest rates, and economic indicators. Use mathematical models, such as stochastic calculus and differential equations, to analyze the data and develop a predictive model. The model could be tested and refined using historical data and validated using real-time data. The output would be a model that can be used to predict the behavior of the financial market and inform investment decisions.

51 - Investigating the properties of different types of complex systems and their behavior, such as network dynamics, agent-based models, or game theory.

Develop a simulation model for each type of complex system being investigated. The model would need to incorporate the relevant variables and interactions between agents or components of the system. The behavior of the system could then be observed and analyzed under different conditions or scenarios. This would allow for a better understanding of the properties and dynamics of each type of complex system and how they may behave in real-world situations.

52 - Analyzing the behavior of different types of partial differential equations and their applications in physics and engineering.

Conduct a literature review to identify different types of partial differential equations and their applications in physics and engineering. Develop mathematical models to simulate the behavior of these equations and analyze their solutions using numerical methods. The results of the analysis could be used to gain insights into the behavior of physical systems and to develop new technologies or improve existing ones. Examples of applications could include fluid dynamics, heat transfer, and electromagnetic fields.

53 - Developing a model to predict the behavior of a fluid using fluid dynamics.

Use computational fluid dynamics software to create a model of the fluid system being studied. The software would simulate the behavior of the fluid under different conditions, such as changes in flow rate or temperature. The model could be validated by comparing its predictions to experimental data. Once validated, the model could be used to predict the behavior of the fluid under different conditions, such as changes in the geometry of the system or the addition of different chemicals. These predictions could be used to optimize the design and operation of the fluid system.

54 - Investigating the properties of different types of geometric objects, such as manifolds or curves, and their applications in geometry and physics.

Conduct a literature review to gather information on the properties of different geometric objects and their applications in geometry and physics. This could involve researching existing theories and models, as well as conducting experiments or simulations to test these theories. The findings could then be analyzed and synthesized to draw conclusions about the properties of different geometric objects and their potential applications in various fields. This could also involve developing new theories or models based on the findings.

55 - Analyzing the behavior of different types of stochastic processes, such as random walks or Markov chains, and their applications in probability theory and statistics.

Conduct simulations of different stochastic processes using software such as R or Python. Analyze the behavior of the simulations and compare them to theoretical predictions. Use the results to draw conclusions about the properties of the different stochastic processes and their applications in probability theory and statistics. Additionally, explore real-world examples of stochastic processes, such as stock prices or weather patterns, and analyze their behavior using the concepts learned from the simulations.

56 - Developing a model to predict the behavior of a biological system using mathematical biology, such as population dynamics, epidemiology, or ecology.

Collect data on the biological system being studied, such as population size, birth and death rates, and environmental factors. Use this data to develop a mathematical model that can predict the behavior of the system over time. The model can be tested and refined using additional data and compared to real-world observations to ensure its accuracy. This model could be used to make predictions about the future behavior of the system, such as the spread of a disease or the impact of environmental changes on a population.

57 - Investigating the properties of different types of wave phenomena, such as sound waves or electromagnetic waves, and their applications in physics and engineering.

Conduct experiments to study the properties of different types of wave phenomena, such as frequency, wavelength, amplitude, and speed. These experiments could involve using instruments such as oscilloscopes, microphones, and antennas to measure and analyze the waves. Applications of these wave phenomena could include designing communication systems, medical imaging technologies, and musical instruments. The results of these experiments could be presented in a report or presentation, highlighting the key findings and their significance in physics and engineering.

58 - Analyzing the behavior of different types of optimization problems in dynamic environments, such as optimal control or dynamic programming.

Conduct simulations of different optimization algorithms in dynamic environments, using various scenarios and parameters to test their performance. The results could be analyzed to determine which algorithms are most effective in different types of dynamic environments and under what conditions. This information could be used to develop more efficient and effective optimization strategies for real-world applications.

59 - Developing a model to predict the behavior of a social network using social network analysis, such as centrality measures, community detection, or opinion dynamics.

Collect data on the social network, such as the number of connections between individuals, the frequency and content of interactions, and any changes in the network over time. Use social network analysis techniques to identify patterns and trends in the data, such as the most influential individuals, the formation of subgroups or communities, and the spread of opinions or behaviors. Develop a model based on these findings that can predict future behavior or changes in the network. The model could be tested and refined using additional data or by comparing its predictions to real-world outcomes.

60 - Investigating the properties of different types of algebraic curves and surfaces, such as elliptic curves or algebraic varieties, and their applications in algebraic geometry.

Conduct a literature review to gather information on the properties of different types of algebraic curves and surfaces. Use mathematical software to generate and analyze examples of these curves and surfaces. Explore their applications in algebraic geometry, such as in cryptography or coding theory. Present findings in a research paper or presentation.

61. What are Interdisciplinary Approaches in Mathematics IA?

With the increasing focus on interdisciplinary learning, students are encouraged to link their Mathematics IA with subjects such as economics, environmental science, and computer science. This approach not only enriches the mathematical exploration but also allows students to showcase their ability to connect concepts across different fields.

How can I score highly?

Scoring highly in the mathematics internal assessment in the IB requires a combination of a thorough understanding of mathematical concepts and techniques, effective problem-solving skills, and clear and effective communication.

To achieve a high score, students should start by choosing a topic that interests them and that they can explore in depth. They should also take the time to plan and organize their report, making sure to include a clear introduction, a thorough development, and a thoughtful conclusion. The introduction in particular should demonstrate students’ genuine personal engagement with the topics.

An IB tutor in Hong Kong said:

"One important aspect that students ignore is that they should pay attention to the formal presentation and mathematical communication, making sure to use proper mathematical notation, correct grammar and spelling, and appropriate use of headings and subheadings."

Finally, students should make sure to engage with the problem and reflect on their own learning, and also make connections between different mathematical concepts and techniques. If they feel difficulty in these, then taking the help of an IB tutor can prove to be quite beneficial.

By following these steps, students can increase their chances of scoring highly on their mathematics internal assessment and contribute positively to their overall grade in the IB Mathematics course.

Need help from an expert?

The world’s top online tutoring provider trusted by students, parents, and schools globally.

Study and Practice for Free

Trusted by 100,000+ Students Worldwide

Achieve Top Grades in your Exams with our Free Resources.

Practice Questions, Study Notes, and Past Exam Papers for all Subjects!

Need Expert Help?

If you’re looking for assistance with IB Maths, get in touch with the TutorChase team and we’ll be able to provide you with an expert IB Maths tutor . We’ll be there every step of the way!

Professional tutor and Cambridge University researcher

Written by: Charles Whitehouse

Charles scored 45/45 on the International Baccalaureate and has six years' experience tutoring IB and IGCSE students and advising them with their university applications. He studied a double integrated Masters at Magdalen College Oxford and has worked as a research scientist and strategy consultant.

Related Posts

Is IB Maths Hard?

IB Chemistry IA: 60 Examples and Guidance

IB Physics IA: 60 Examples and Guidance

Hire a tutor

Please fill out the form and we'll find a tutor for you

• Select your country
• Afghanistan
• Åland Islands
• American Samoa
• Antigua and Barbuda
• Bosnia and Herzegovina
• Bouvet Island
• British Indian Ocean Territory
• Brunei Darussalam
• Burkina Faso
• Cayman Islands
• Central African Republic
• Christmas Island
• Cocos (Keeling) Islands
• Congo, The Democratic Republic of the
• Cook Islands
• Cote D'Ivoire
• Czech Republic
• Dominican Republic
• El Salvador
• Equatorial Guinea
• Falkland Islands (Malvinas)
• Faroe Islands
• French Guiana
• French Polynesia
• French Southern Territories
• Guinea-Bissau
• Heard Island and Mcdonald Islands
• Holy See (Vatican City State)
• Iran, Islamic Republic Of
• Isle of Man
• Korea, Democratic People'S Republic of
• Korea, Republic of
• Lao People'S Democratic Republic
• Libyan Arab Jamahiriya
• Liechtenstein
• Macedonia, The Former Yugoslav Republic of
• Marshall Islands
• Micronesia, Federated States of
• Moldova, Republic of
• Netherlands
• Netherlands Antilles
• New Caledonia
• New Zealand
• Norfolk Island
• Northern Mariana Islands
• Palestinian Territory, Occupied
• Papua New Guinea
• Philippines
• Puerto Rico
• Russian Federation
• Saint Helena
• Saint Kitts and Nevis
• Saint Lucia
• Saint Pierre and Miquelon
• Saint Vincent and the Grenadines
• Sao Tome and Principe
• Saudi Arabia
• Serbia and Montenegro
• Sierra Leone
• Solomon Islands
• South Africa
• South Georgia and the South Sandwich Islands
• Svalbard and Jan Mayen
• Switzerland
• Syrian Arab Republic
• Taiwan, Province of China
• Tanzania, United Republic of
• Timor-Leste
• Trinidad and Tobago
• Turkmenistan
• Turks and Caicos Islands
• United Arab Emirates
• United Kingdom
• United States
• United States Minor Outlying Islands
• Virgin Islands, British
• Virgin Islands, U.S.
• Wallis and Futuna
• Western Sahara

Alternatively contact us via WhatsApp, Phone Call, or Email

Simple and Manageable IB Math IA Topics

Hey there, fellow IB procrastinator! So, you’ve been putting off choosing a topic for your Math IA, and now you’re in full panic mode. Don’t worry, I’ve got your back. Let’s dive into some of the easiest IB Math IA ideas that will help you get that assignment done and dusted. Plus, I’ll tell you how RevisionDojo can be your secret weapon to ace your IA and boost your grades.

1. Golden Ratio in Nature and Architecture

• What’s the Deal: The Golden Ratio (around 1.618) pops up everywhere—in flowers, seashells, and even famous buildings. You can measure and analyze these proportions to see if they fit the Golden Ratio.
• Why It’s Easy: Tons of resources and examples are out there. Plus, measuring stuff isn’t too tough and can be pretty fun.

2. Mathematics of Music

• What’s the Deal: Dive into how math and music are connected. You could explore the frequencies of musical notes, the math behind scales, or patterns in different music genres.
• Why It’s Easy: This topic is creative and doesn’t require super complex math. You’ll get to mix your love for music with some cool math concepts.

3. Fibonacci Sequence in Nature

• What’s the Deal: The Fibonacci sequence appears in nature, like in the arrangement of leaves or the pattern of seeds in a sunflower. You’ll count and analyze these natural patterns.
• Why It’s Easy: The sequence is simple to understand and easy to spot in nature. Plus, it’s super interesting to see math in the world around you.

4. Mathematics of Games and Puzzles

• What’s the Deal: Look into the math behind your favorite games or puzzles. Analyze probability in card games, strategies in chess, or patterns in Sudoku.
• Why It’s Easy: Games are fun and engaging, and the math involved is usually straightforward. It’s a win-win!

5. Statistics in Sports

• What’s the Deal: Use stats to analyze data from your favorite sport. Look at player performance, team stats, or game outcomes.
• Why It’s Easy: Sports stats are easy to find and work with. Plus, if you love sports, this will keep you interested and motivated.

6. Symmetry in Art and Nature

• What’s the Deal: Investigate different types of symmetry in art or nature. Analyze patterns in wallpaper designs, tiling, or the symmetrical structure of flowers and animals.
• Why It’s Easy: Symmetry is visually intuitive and the math is often straightforward. You’ll get to appreciate the beauty in math.

7. Mathematical Patterns in Pascal’s Triangle

• What’s the Deal: Explore various patterns in Pascal’s Triangle, like binomial coefficients, the Fibonacci sequence, or prime numbers. Discuss their significance and applications.
• Why It’s Easy: Pascal’s Triangle is easy to construct and analyze, with plenty of well-documented patterns to explore.

8. Cryptography and Basic Encryption Methods

• What’s the Deal: Look into simple cryptographic techniques like Caesar ciphers or substitution ciphers. Explain how these methods encrypt and decrypt information.
• Why It’s Easy: Basic cryptographic methods are straightforward and fun to play around with. This topic is fascinating and accessible.

9. Population Growth Models

• What’s the Deal: Study mathematical models of population growth, such as linear, exponential, or logistic growth. Apply these models to real-world data and analyze the results.
• Why It’s Easy: The math concepts are simple to grasp and apply. Plus, real-world data is readily available.

10. Exploring Probability with Everyday Activities

• What’s the Deal: Conduct experiments to explore probability in everyday activities like rolling dice, flipping coins, or drawing cards. Compare theoretical vs. experimental probability.
• Why It’s Easy: Probability experiments are easy to set up and analyze. The math involved is basic but can be very revealing.

Choosing Your IA Topic and Making It a Success

Now that you’ve got some ideas, let’s talk about how to choose the best IA topic and ensure it scores high. The best scoring IA isn’t just about picking an easy topic—it’s about how you handle and present your work. Here are some IA tips to help you out:

Structure and Time Management: A well-structured IA is key to scoring high. Start by outlining your IA with clear sections—introduction, methodology, analysis, and conclusion. Break down your work into smaller tasks and set deadlines for each part. This will help you manage your time effectively and avoid last-minute stress.

RevisionDojo to the Rescue: Now, here’s how RevisionDojo can turn your IA from good to great. RevisionDojo provides detailed guides that break down each part of the IA, so you know exactly what to do and when to do it. With step-by-step instructions, you’ll never feel lost. Plus, they offer high-scoring examples that show you what excellence looks like, giving you a clear benchmark to aim for.

Feedback and Refinement: One of the best features of RevisionDojo is the feedback system. Submit your drafts and get constructive criticism from peers or professional reviewers. This helps you refine your work, ensuring it’s polished and ready for submission.

Practice and Polishing: Use RevisionDojo’s resources to practice your math skills and polish your IA. Their tools can help you iron out any errors and present your work in the best possible light.

Time Management Tools: Struggling to keep track of everything? RevisionDojo’s time management tools can help you plan your work and stick to a schedule, making it easier to stay on top of your workload without feeling overwhelmed.

By leveraging RevisionDojo, you’ll have all the support you need to make your IA not just good, but great. So, take a deep breath, pick a topic that excites you, and dive in with confidence. With RevisionDojo by your side, you’re set to crush your IA and boost your grades. You’ve got this!

Ace your exams with RevisionDojo

• Thousands of practice questions
• Study notes and flashcards for every topic and subject
• Free Jojo AI tutor

RevisionDojo, saved my exams. I went from a 4 to a 6 in math, a 5 to a 7 in econ and a 5 to a 7 in chem. ”

Joseph Chan

IBDP student

Rated Excellent

On Trustpilot

• Mathematics: AA SL
• Mathematics: AA HL
• Mathematics: AI SL
• Mathematics: AI HL
• Biology SL (FE2025)
• Biology HL (FE2025)
• Biology SL (FE2016)
• Biology HL (FE2016)
• Chemistry SL (FE2025)
• Chemistry HL (FE2025)
• Chemistry SL (FE2016)
• Chemistry HL (FE2016)
• Physics SL (FE2025)
• Physics HL (FE2025)
• Physics SL (FE2016)
• Physics HL (FE2016)
• Business SL (FE2024)
• Business HL (FE2024)
• Business SL (FE2016)
• Business HL (FE2016)
• Economics SL
• Economics HL
• Psychology SL
• Psychology HL
• Computer Science SL
• Computer Science HL
• English A LAL SL
• English A LAL HL

20 Amazing Mathematics IA Ideas to ace your IBDP

One fact about students hating Mathematics is considering it boring, Usually, IB students view Maths as an inappropriate subject so they strive hard to understand all those equations and formulas. Hard as a subject itself, some of the students even find confusing how to pick a good Mathematics IA topic?

But, Blen got you!

We have assembled 20 best Maths IA topics to make things easy for you.

• Pythagorean triples:  Find out three numbers that can form a Pythagorean triple.
• Pascal's Triangle: Discover pattern by using Pascal's triangle array of numbers.

Probability and Number Theory 

• Chinese Remainder Theorem:  Determine the remainder of the division of n by the product of integer values.
• Birthday problem:  Find the probability of how many people share the same birthday if placed in the same room?
• Monty Hall problem:  Explore how Baye’s rule is used in real life as in given problem.
• Probability: Find out how Oxford and Cambridge are biased towards state-school applicants?
• Traffic flow:  How do mathematical applications work in traffic jams?
• Radioactive decay modelling:  How long Chernobyl will take to become safe for a living?
• Modelling:  Can musical notes or dissonance be mathematically modeled?
• Egg shape modelling:  Calculate the surface area and volume of an egg by mathematical applications.
• Virus spreading:  Find out how long will it take for the whole world to wipe out if a deadly virus breaks out?
• Modelling: How does tea in the cup cool down?

Series and Sequences

• Prove that the sum of all positive integers is -1/12 through series and sequences.

Integration and Derivation

• Gini coefficient: Derive Gini coefficient for some countries using integration approach, if explicitly compared their level of economic inequality.

Optimization Strategy

• Area Optimization:  Use strategies to optimize the area of a polygon.
• Volume Optimization:  Find the maximum volume of a cuboid to some constraint.
• Stacking Balls: Let's assume you want to place balls on cardboard, what is the optimal method to use the space effectively? 
• Wobbly Tables:  Due to uneven grounds mostly tables are wobbly; can you find a way of orienting tables to make them stable?
• Prisoner's dilemma problem:  By using game theory deduce the optimal strategy for the prisoner's dilemma.
• Tic Tac Toe: Find the optimal strategy used in this game, does your probability of winning boost up by some move?

Disclaimer: Topics suggested in this article are only for the motivational purpose and to give students some ideas of how they can link some real-world investigations with IB Maths internal assessment to secure a good grade. 

One Subscription, for All Your IBDP Subjects

Unrestricted access to IBDP Exam-style questions, key concepts, mock test, performance score cards and more…

One FREE student Account with Unrestricted access to IBDP Exam-style questions, key concepts, mock test, assignment, student analytics and more…

What innovative concepts can be explored for an IB Economics IA?

Navigating the environmental systems and societies (ess) ia, mastering the ib english oral commentary, an ultimate handbook for ib math internal assessment (ia), a comprehensive guide to choosing history ia topics, unveiling the perfect economics ia: exploring real-world applications, a comprehensive manual for crafting ib psychology internal assessment (ia), stuck for ideas for your chemistry ia.

Blen is an interactive, auto-graded platform for IBDP students, teachers, and schools. It provides curriculum-aligned content, interactive questions, adaptive mock tests, assignments, and detailed reports to help unlock IBDP potential.

Be the first to know about our news and special offers direct to your inbox.

I consent to the processing of my personal data, in order to receive news and updates of Blen, according to the " Privacy Statement "

• Find A Tutor
• Geneva Tutors
• Lausanne Tutors
• Zurich Tutors
• Basel Tutors
• Online Tutors
• Maths Tutors
• Chemistry Tutors
• Physics Tutors
• Biology Tutors
• English Tutors
• History Tutors
• Geography Tutors
• Language Tutors
• Special Educational Needs
• Residential Tutors
• Primary School
• School Entrance Exams
• Middle School
• Combined Science
• Maths AA and AI
• IB Internal Assessment
• Environmental Systems & Societies (ESS)
• Sports, Exercise & Health Science
• Computer Science
• Global Politics
• Digital Society
• Business Management
• Visual Arts
• English A/B
• English Oral (IO)
• German Oral (IO)
• French Oral (IO)
• Spanish A/B
• French Ab Initio
• German Ab Initio
• Spanish Ab Initio
• IB Extended Essay
• IB Theory of Knowledge
• University Applications
• Our Approach
• Happy Parents
• School Choice
• Become a Tutor

How to choose your Maths IA topic

By TutorsPlus

The Maths IA accounts for a big chunk of your final score (20%). Plus, if you do well, these points are in the bag before you even step into the exam hall.

You can see why it is worth putting in the effort to choose the right Maths IA subject, right?

But like many students, it is common to struggle when trying to choose the best topic.

Fear not!  We are here to help.  Click here to reach our IB Maths teachers & examiners for help with your IA, or just the topic choice and question to allow you to get the best grade possible.

Like our tutor Vineet, one of our IB Maths IA Examiners and certified IB teacher. In this article, he takes you through the steps you need to follow to choose the best Maths IA topic for you.

He knows what is talking about, as he has taught IB Maths in international schools in New Zealand, Russia, and also China, and specialises in teaching Maths IAs.

But how do you choose the right topic for your Maths IA?

So we know that the IA is an individual piece of research undertaken by the student and requires students to explore an aspect of mathematics at a deeper level. But most importantly, the IA is not a separate project, it is an integral part of your learning.

Actually, you will find that every Maths topic you are learning has the potential to develop an IA topic.

If any of the five topics tickle your mathematical curiosity you can start working on your IA topic as early as in Grade 11.

However, I recommend starting when you have had a full explanation of the requirements from your class teacher.  But, most importantly, do stick to the deadlines that they give you.

Above all, this is to avoid you becoming overwhelmed by deadlines crashing together in your IB2 year.

Should I use one of the online lists to help me?

As an examiner, I want to see the aspect of personal interest in an IA.  As a rule, the more individual the topic is, the more care and attention the student tends to put into the work. So, I would recommend not using one of the published lists.  By the very fact that it is on the internet thousands of students will have looked at them and chosen the same topics.  Think of the poor examiner come marking time!

Also, the subject needs to interest you.  After all, you’re going to spend a lot of time working on it.  There may be better ways of selecting an area of mathematical exploration that you are going to write 6-12 pages about than choosing from someone else’s list.

It shouldn’t be too narrow or too broad.

Sometimes this feels like an impossible balance when choosing a Maths IA topic.  But, perhaps this can help.

It needs to be broad enough that your essay can answer all the criteria of the marking criteria.  So check any potential topics against the in-depth rubric , a simplified version is here below.

Example exploring IA topics for Algebra and Number

So I can make this a little bit clearer, let’s give you an example of an IA topic below that can be developed while you are studying Algebra & Number. At the same time, I have outlined the steps to go through when deciding what is the best IA Maths topic for you.

How to Come Up With Unique IA Math Topics: Examples and Steps that Work

Here are some other tips on how to choose unique IA Math topics.

Brainstorm IA ideas

When trying to choose your own IA topic you can brainstorm potential ideas within the course topics that most interest you.

Binomial theorem is one of the subtopics of Algebra and there are so many interesting aspects of binomial theorem that can be explored in much detail.

Binomial theorem – IA options exploration – Brainstorm

• You could look at Pascal’s triangle and patterns in Pascal’s triangle to start with.
• Almost everything in Math can be proved unless it is an axiom? So why not prove Binomial theorem. The proof of this theorem is an HL topic which uses mathematical induction to prove this result. However, to be able to use mathematical induction you need to have a conjecture and you could develop/ form a conjecture which is neither sighted in SL nor in HL? Once a conjecture is formed you could either use induction or could use Calculus to prove this theorem.
• You could look at the binomial theorem for rational exponents.
• De Moivre’s theorem is a case of binomial and it can be seen as an application of this theorem within mathematics?
• If you looked at extending binomial expansions to trinomial expansions, you will find some interesting ideas such as Pascal’s pyramid.

Seek Guidance from Your Teacher

Your teacher is your first point of contact. As a curriculum expert, they can help you understand whether your topic meets the programme’s requirements. Moreover, they know your strengths and weaknesses as a math student. Hence, they are able to evaluate whether this topic is manageable.

The next tip is listen to their advice! As the IAs are internally assessend, as the name suggests, they have likely been marking IAs for years. Above all, they know if you are choosing a sensible topic. So, like it or not, we recommend you listen to their suggestions.

Do Your Research

Don’t settle on the first topic that comes to mind. It is better to choose between several options. For inspiration, you can check online resources, libraries, and past Math IAs . Besides, past projects can offer valuable insights into expectations and successful approaches.

When you have a few options to choose from, ask yourself two questions:

Which IA Math topics are the most interesting for me?

Do they provide enough material for a comprehensive IA? If you choose a topic you find interesting and engaging it will come through in your work.

Showcase Your Passion

IA is not just another assignment. Is your opportunity to explore mathematical concepts that excite you. The best topic for your IA is one that sparks your curiosity and allows for applying your knowledge with a deeper understanding.

Remember, to earn marks for Personal Engagement, your work should explain why you chose this particular topic. Maybe you’ve always been a basketball fan and wanted to understand the secrets behind the perfect free throw. That’s why in your IA, you’d like to analyse how the angle of release, the force applied, and the trajectory of the ball all work together to influence the success of a shot.

Choosing an interesting AI Math topic is important not only to maximise your score. It will also help make the research and writing process more enjoyable.

Prioritise Feasibility

While uniqueness is important, the chosen topic should also be easy to explore.

Many students believe that they need something above the IB level to impress their examiners. However, this path is risky. First of all, complex concepts may be too hard to grasp with your current level of Maths comprehension. And if you fail to understand something, your IA may end up weak, shallow, or riddled with errors. Second, do you really have the time and resources to complete a challenging task? Do you have access to the necessary information? Finally, you will not pick up extra marks as they ask for Maths at the expected level of the IB.

If there seem to be too many obstacles, it is wise to try a different path.

Seek Expert Support

If you find yourself struggling to find a suitable topic or navigate through the research and writing process, consider getting support from a professional tutor.

At TutorsPlus , we are happy to become your partner in navigating the challenge of Math IA. Our expertise can guide you to identify efficient data analysis or collection methods. We can also suggest additional resources and ways to improve your work to meet the IA criteria.

A final thought

IA stimulus could come from other learning disciplines such as Economics, Geography, Physics, Biology or Sports can be intriguing or appear more exciting. However, based on my experience of over 10 years as an IB Math HL/ SL teacher, and an IA Maths Examiner, if it’s a Math IA then surprise, surprise it should revolve around Maths. Maths is the main actor. Criteria E: Use of Mathematics that has the highest marks among other criteria.

Finally, if you are still feeling lost or confused why not work with one of our tutors to help find the best IA topic for you?  Here is some more information about our IA specialist tutors across all IB subjects.

Either one-to-one or by joining one of our online group courses you needn’t feel at a loss. Vineet is an IB Maths Examiner, and certified teacher. He has taught in international schools in New Zealand, Russia, and also China. At the same time, he specialises in teaching Maths IAs.

Vineet is a highly experienced maths teacher and IB examiner. If you would like tuition with Vineet, get in touch at [email protected] or fill out the form below.

For more details on the IB Diploma Maths course visit the IBO page .

Sara has been an education consultant for TutorsPlus for 15 years, and is an expert on international IB education.  She is also a parent of two lively children.

Find a Tutor

Popular Posts

English IO – How to Ace Your IB English Literature & Language Oral

Tips to get a Top Grade in Your IGCSE English

How to get a top score in your IB TOK Exhibition

IGCSE Maths Revision Tips To Help You Today

What is the IA, EE or TOK? Everything you need to know about the IB written assignments

Maths Anxiety – How Parents Can Help 

More articles from our expert tutors.

Why handwriting is still important

Full Guide to IB Economics Internal Assessment (IA)

The Best IGCSE Chemistry Tips to Crush Your Exam

Find a Tutor Today

" * " indicates required fields

Step 1 of 5

Find the best support for your family

• International
• Topical and themed
• Early years
• Special needs
• Schools directory
• Resources Jobs Schools directory News Search

Tes Maths: Projects, investigations and enrichment tasks

Tes resources team.

Take a trip off-plan and get creative with your maths lessons with projects, investigation ideas and enrichment tasks

As the final half-term of the school year approaches, there may be time to do something slightly different in your maths lessons. Perhaps an investigation to apply the knowledge and skills students have acquired over the year, a project to allow them to work creatively as a team to produce something special, or an enrichment activity to show students just how interesting maths can be. Whatever you have in mind, explore this selection of resources from the Tes community for some inspiration.

Investigations

Investigations offer an opportunity for students to pull together the skills and knowledge they have learned over the course of the year and to apply them in a different context.

Maths Investigations

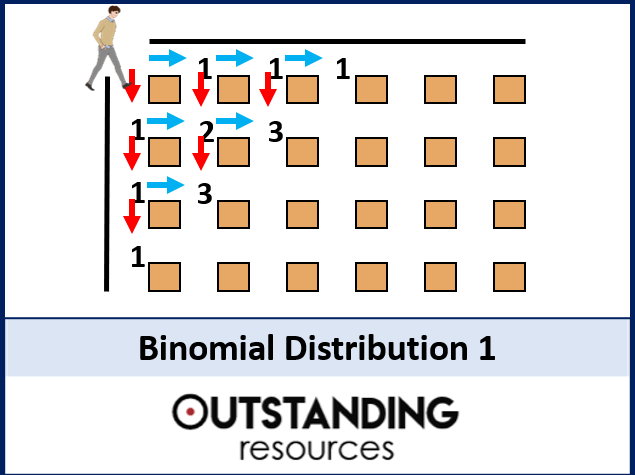
Binomial Distribution Investigation

Assorted Investigations

3D enlargement investigation

Angles in polygons investigation

Much like investigations, projects prompt pupils to use and apply their knowledge, often with the option to work as part of a team in a fun context.

Build the School Project

Functional Mathematics: Design a Bedroom

DATA PROJECT

Make A Million - Maths Housing Design Project

KS3 Finance/Investment/Business Maths Project

The end of the year is the perfect time to stop worrying about whether something is on the GCSE/IGCSE or A-level syllabus and to challenge students with some interesting mathematics.

Theme Park - Enrichment Activities

Creativity in Maths

Emergency maths cover lesson? Enrichment materials

Fermi Estimation