grade 5 module 5 lesson 9 homework answer key

Eureka Math Grade 5 Module 3 Lesson 9 Answer Key

Engage ny eureka math 5th grade module 3 lesson 9 answer key, eureka math grade 5 module 3 lesson 9 sprint answer key.

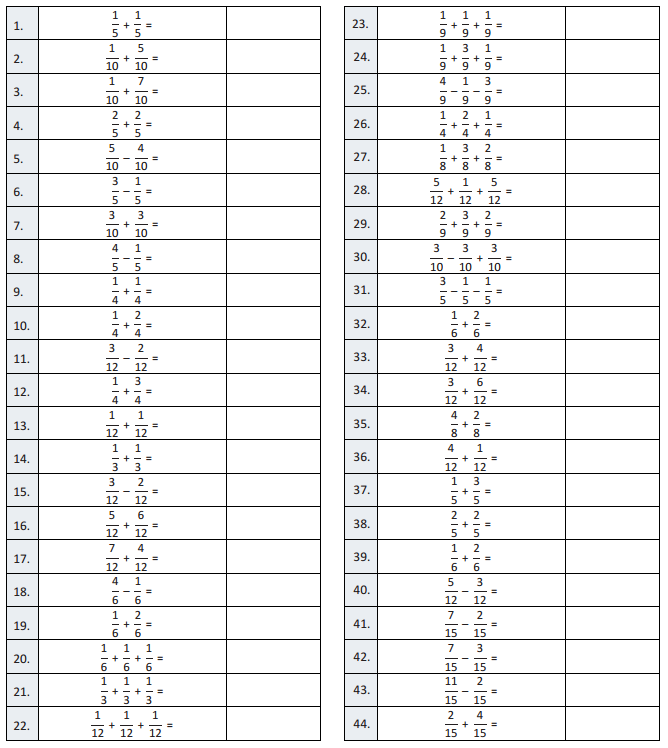
Question 1. \(\frac{1}{5}\) + \(\frac{1}{5}\) = Answer: \(\frac{1}{5}\) + \(\frac{1}{5}\) = \(\frac{2}{5}\)

Question 2. \(\frac{1}{10}\) + \(\frac{5}{10}\) = Answer: \(\frac{1}{10}\) + \(\frac{5}{10}\) = \(\frac{6}{10}\) = \(\frac{3}{5}\)

Question 3. \(\frac{1}{10}\) + \(\frac{7}{10}\) = Answer: \(\frac{1}{10}\) + \(\frac{7}{10}\) = \(\frac{8}{10}\) = \(\frac{4}{5}\)

Question 4. \(\frac{2}{5}\) + \(\frac{2}{5}\) = Answer: \(\frac{2}{5}\) + \(\frac{2}{5}\) = \(\frac{4}{5}\)

Question 5. \(\frac{5}{10}\) – \(\frac{4}{10}\) = Answer: \(\frac{5}{10}\) – \(\frac{4}{10}\) = \(\frac{1}{10}\)

Question 6. \(\frac{3}{5}\) – \(\frac{1}{5}\) = Answer: \(\frac{3}{5}\) – \(\frac{1}{5}\) = \(\frac{2}{5}\)

Question 7. \(\frac{3}{10}\) + \(\frac{3}{10}\) = Answer: \(\frac{3}{10}\) + \(\frac{3}{10}\) = \(\frac{6}{10}\) = \(\frac{3}{5}\)

Question 8. \(\frac{4}{5}\) – \(\frac{1}{5}\) = Answer: \(\frac{4}{5}\) – \(\frac{1}{5}\) = \(\frac{3}{5}\)

Question 9. \(\frac{1}{4}\) + \(\frac{1}{4}\) = Answer: \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\)

Question 10. \(\frac{1}{4}\) + \(\frac{2}{4}\) = Answer: \(\frac{1}{4}\) + \(\frac{2}{4}\) = \(\frac{3}{4}\)

Question 11. \(\frac{3}{12}\) – \(\frac{2}{12}\) = Answer: \(\frac{3}{12}\) – \(\frac{2}{12}\) = \(\frac{1}{12}\)

Question 12. \(\frac{1}{4}\) + \(\frac{3}{4}\) = Answer: \(\frac{1}{4}\) + \(\frac{3}{4}\) = \(\frac{4}{4}\) = 1

Question 13. \(\frac{1}{12}\) + \(\frac{1}{12}\) = Answer: \(\frac{1}{12}\) + \(\frac{1}{12}\) = \(\frac{2}{12}\) = \(\frac{1}{6}\)

Question 14. \(\frac{1}{3}\) + \(\frac{1}{3}\) = Answer: \(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{2}{3}\)

Question 15. \(\frac{3}{12}\) – \(\frac{2}{12}\) = Answer: \(\frac{3}{12}\) – \(\frac{2}{12}\) = \(\frac{1}{12}\)

Question 16. \(\frac{5}{12}\) + \(\frac{6}{12}\) = Answer: \(\frac{5}{12}\) + \(\frac{6}{12}\) = \(\frac{11}{12}\)

Question 17. \(\frac{7}{12}\) + \(\frac{4}{12}\) = Answer: \(\frac{7}{12}\) + \(\frac{4}{12}\) = \(\frac{11}{12}\)

Question 18. \(\frac{4}{6}\) – \(\frac{1}{6}\) = Answer: \(\frac{4}{6}\) – \(\frac{1}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

Question 19. \(\frac{1}{6}\) + \(\frac{2}{6}\) = Answer: \(\frac{1}{6}\) + \(\frac{2}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

Question 20. \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = Answer: \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{3}{6}\) =  \(\frac{1}{2}\)

Question 21. \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) = Answer: \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{3}{3}\) = 1

Question 22. \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) = Answer: \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)

Question 23. \(\frac{1}{9}\) + \(\frac{1}{9}\) + \(\frac{1}{9}\) = Answer: \(\frac{1}{9}\) + \(\frac{1}{9}\) + \(\frac{1}{9}\) = \(\frac{3}{9}\) =  \(\frac{1}{3}\)

Question 24. \(\frac{1}{9}\) + \(\frac{3}{9}\) + \(\frac{1}{9}\) = Answer: \(\frac{1}{9}\) + \(\frac{3}{9}\) + \(\frac{1}{9}\) = \(\frac{5}{9}\)

Question 25. \(\frac{4}{9}\) – \(\frac{1}{9}\) – \(\frac{3}{9}\) = Answer: \(\frac{4}{9}\) – \(\frac{1}{9}\) – \(\frac{3}{9}\) = \(\frac{8}{9}\)

Question 26. \(\frac{1}{4}\) + \(\frac{2}{4}\) + \(\frac{1}{4}\) = Answer: \(\frac{1}{4}\) + \(\frac{2}{4}\) + \(\frac{1}{4}\) = \(\frac{4}{4}\) = 1

Question 27. \(\frac{1}{8}\) + \(\frac{3}{8}\) + \(\frac{2}{8}\) = Answer: \(\frac{1}{8}\) + \(\frac{3}{8}\) + \(\frac{2}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)

Question 28. \(\frac{5}{12}\) + \(\frac{1}{12}\) + \(\frac{5}{12}\) = Answer: \(\frac{5}{12}\) + \(\frac{1}{12}\) + \(\frac{5}{12}\) = \(\frac{11}{12}\)

Question 29. \(\frac{2}{9}\) + \(\frac{3}{9}\) + \(\frac{2}{9}\) = Answer: \(\frac{2}{9}\) + \(\frac{3}{9}\) + \(\frac{2}{9}\) = \(\frac{7}{9}\)

Question 30. \(\frac{3}{10}\) – \(\frac{3}{10}\) + \(\frac{3}{10}\) = Answer: \(\frac{3}{10}\) – \(\frac{3}{10}\) + \(\frac{3}{10}\) = \(\frac{9}{10}\)

Question 31. \(\frac{3}{5}\) – \(\frac{1}{5}\) – \(\frac{1}{5}\) = Answer: \(\frac{3}{5}\) – \(\frac{1}{5}\) – \(\frac{1}{5}\) = \(\frac{3}{5}\) – \(\frac{2}{5}\) = \(\frac{1}{5}\)

Question 32. \(\frac{1}{6}\) + \(\frac{2}{6}\) = Answer: \(\frac{1}{6}\) + \(\frac{2}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\) =\

Question 33. \(\frac{3}{12}\) + \(\frac{4}{12}\) = Answer: \(\frac{3}{12}\) + \(\frac{4}{12}\) = \(\frac{7}{12}\)

Question 34. \(\frac{3}{12}\) + \(\frac{6}{12}\) = Answer: \(\frac{3}{12}\) + \(\frac{6}{12}\) = \(\frac{9}{12}\) = \(\frac{3}{4}\)

Question 35. \(\frac{4}{8}\) + \(\frac{2}{8}\) = Answer: \(\frac{4}{8}\) + \(\frac{2}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)

Question 36. \(\frac{4}{12}\) + \(\frac{1}{12}\) = Answer: \(\frac{4}{12}\) + \(\frac{1}{12}\) = \(\frac{5}{12}\)

Question 37. \(\frac{1}{5}\) + \(\frac{3}{5}\) = Answer: \(\frac{1}{5}\) + \(\frac{3}{5}\) = \(\frac{4}{5}\)

Question 38. \(\frac{2}{5}\) + \(\frac{2}{5}\) = Answer: \(\frac{2}{5}\) + \(\frac{2}{5}\) = \(\frac{4}{5}\)

Question 39. \(\frac{1}{6}\) + \(\frac{2}{6}\) = Answer: \(\frac{1}{6}\) + \(\frac{2}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

Question 40. \(\frac{5}{12}\) – \(\frac{3}{12}\) = Answer: \(\frac{5}{12}\) – \(\frac{3}{12}\) = \(\frac{2}{12}\) = \(\frac{1}{6}\)

Question 41. \(\frac{7}{15}\) – \(\frac{2}{15}\) = Answer: \(\frac{7}{15}\) – \(\frac{2}{15}\) = \(\frac{5}{15}\) = \(\frac{1}{3}\)

Question 42. \(\frac{7}{15}\) – \(\frac{3}{15}\) = Answer: \(\frac{7}{15}\) – \(\frac{3}{15}\) = \(\frac{4}{15}\)

Question 43. \(\frac{11}{15}\) – \(\frac{2}{15}\) = Answer: \(\frac{11}{15}\) – \(\frac{2}{15}\) = \(\frac{9}{15}\)

Question 44. \(\frac{2}{15}\) + \(\frac{4}{15}\) = Answer: \(\frac{2}{15}\) + \(\frac{4}{15}\) = \(\frac{6}{15}\) = \(\frac{2}{5}\)

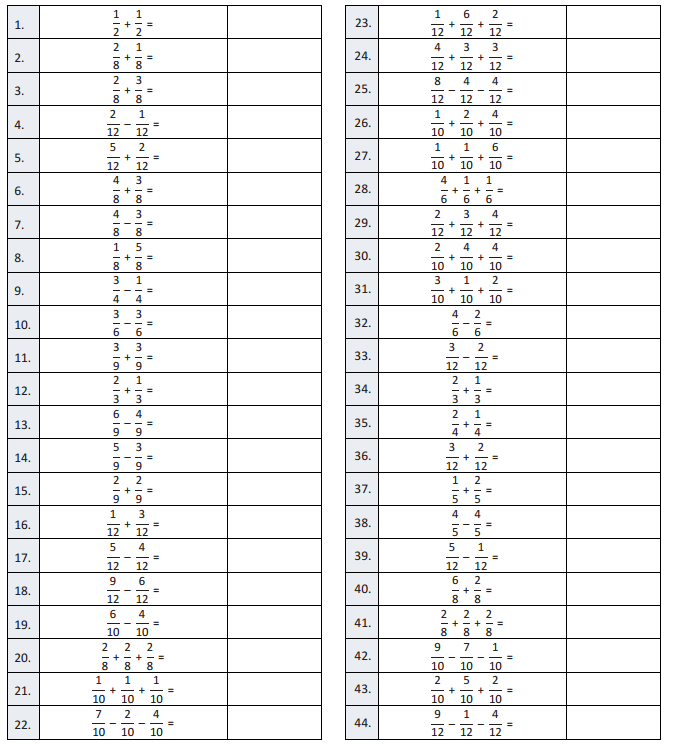
Question 1. \(\frac{1}{2}\) + \(\frac{1}{2}\) = Answer: \(\frac{1}{2}\) + \(\frac{1}{2}\) = \(\frac{2}{2}\) = 1

Question 2. \(\frac{2}{8}\) + \(\frac{1}{8}\) = Answer: \(\frac{2}{8}\) + \(\frac{1}{8}\) = \(\frac{3}{8}\)

Question 3. \(\frac{2}{8}\) + \(\frac{3}{8}\) = Answer: \(\frac{2}{8}\) + \(\frac{3}{8}\) = \(\frac{5}{8}\)

Question 4. \(\frac{2}{12}\) – \(\frac{1}{12}\) = Answer: \(\frac{2}{12}\) – \(\frac{1}{12}\) = \(\frac{1}{12}\)

Question 5. \(\frac{5}{12}\) + \(\frac{2}{12}\) = Answer: \(\frac{5}{12}\) + \(\frac{2}{12}\) = \(\frac{7}{12}\)

Question 6. \(\frac{4}{8}\) – \(\frac{3}{8}\) = Answer: \(\frac{4}{8}\) – \(\frac{3}{8}\) = \(\frac{1}{8}\)

Question 7. \(\frac{4}{8}\) – \(\frac{3}{8}\) = Answer: \(\frac{4}{8}\) – \(\frac{3}{8}\) = \(\frac{1}{8}\)

Question 8. \(\frac{1}{8}\) + \(\frac{5}{8}\) = Answer: \(\frac{1}{8}\) + \(\frac{5}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)

Question 9. \(\frac{3}{4}\) – \(\frac{1}{4}\) = Answer: \(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\)

Question 10. \(\frac{3}{6}\) – \(\frac{3}{6}\) = Answer: \(\frac{3}{6}\) – \(\frac{3}{6}\) = 0

Question 11. \(\frac{3}{9}\) + \(\frac{3}{9}\) = Answer: \(\frac{3}{9}\) + \(\frac{3}{9}\) = \(\frac{6}{9}\) = \(\frac{2}{3}\)

Question 12. \(\frac{2}{3}\) + \(\frac{1}{3}\) = Answer: \(\frac{2}{3}\) + \(\frac{1}{3}\) = \(\frac{3}{3}\) = 1

Question 13. \(\frac{6}{9}\) – \(\frac{4}{9}\) = Answer: \(\frac{6}{9}\) – \(\frac{4}{9}\) = \(\frac{2}{9}\)

Question 14. \(\frac{5}{9}\) – \(\frac{3}{9}\) = Answer: \(\frac{5}{9}\) – \(\frac{3}{9}\) = \(\frac{2}{9}\)

Question 15. \(\frac{2}{9}\) + \(\frac{2}{9}\) = Answer: \(\frac{2}{9}\) + \(\frac{2}{9}\) = \(\frac{4}{9}\)

Question 16. \(\frac{1}{12}\) + \(\frac{3}{12}\) = Answer: \(\frac{1}{12}\) + \(\frac{3}{12}\) = \(\frac{4}{12}\) = \(\frac{1}{4}\)

Question 17. \(\frac{5}{12}\) – \(\frac{4}{12}\) = Answer: \(\frac{5}{12}\) – \(\frac{4}{12}\) = \(\frac{1}{12}\)

Question 18. \(\frac{9}{12}\) – \(\frac{6}{12}\) = Answer: \(\frac{9}{12}\) – \(\frac{6}{12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)

Question 19. \(\frac{6}{10}\) – \(\frac{4}{10}\) = Answer: \(\frac{6}{10}\) – \(\frac{4}{10}\) = \(\frac{2}{10}\) = \(\frac{1}{5}\)

Question 20. \(\frac{2}{8}\) + \(\frac{2}{8}\) + \(\frac{2}{8}\) = Answer: \(\frac{2}{8}\) + \(\frac{2}{8}\) + \(\frac{2}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)

Question 21. \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) = Answer: \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) = \(\frac{3}{10}\) +

Question 22. \(\frac{7}{12}\) – \(\frac{2}{10}\) – \(\frac{4}{10}\) = Answer: \(\frac{7}{12}\) – \(\frac{2}{10}\) – \(\frac{4}{10}\) = \(\frac{7}{12}\) – \(\frac{6}{10}\) = \(\frac{1}{10}\)

Question 23. \(\frac{1}{12}\) + \(\frac{6}{12}\) + \(\frac{2}{12}\) = Answer: \(\frac{1}{12}\) + \(\frac{6}{12}\) + \(\frac{2}{12}\) = \(\frac{9}{12}\) = \(\frac{3}{4}\)

Question 24. \(\frac{4}{12}\) + \(\frac{3}{12}\) + \(\frac{3}{12}\) = Answer: \(\frac{4}{12}\) + \(\frac{3}{12}\) + \(\frac{3}{12}\) = \(\frac{10}{12}\) = \(\frac{5}{6}\)

Question 25. \(\frac{8}{12}\) – \(\frac{4}{12}\) – \(\frac{4}{12}\) = Answer: \(\frac{8}{12}\) – \(\frac{4}{12}\) – \(\frac{4}{12}\) = \(\frac{8}{12}\) – \(\frac{8}{12}\) = 0

Question 26. \(\frac{1}{10}\) + \(\frac{2}{10}\) + \(\frac{4}{10}\) = Answer: \(\frac{1}{10}\) + \(\frac{2}{10}\) + \(\frac{4}{10}\) = \(\frac{7}{10}\)

Question 27. \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{6}{10}\) = Answer: \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{6}{10}\) = \(\frac{8}{10}\) = \(\frac{4}{5}\)

Question 28. \(\frac{4}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = Answer: \(\frac{4}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{6}{6}\) = 1

Question 29. \(\frac{2}{12}\) + \(\frac{3}{12}\) + \(\frac{4}{12}\) = Answer: \(\frac{2}{12}\) + \(\frac{3}{12}\) + \(\frac{4}{12}\) = \(\frac{9}{12}\) = \(\frac{3}{4}\)

Question 30. \(\frac{2}{10}\) + \(\frac{4}{10}\) + \(\frac{4}{10}\) = Answer: \(\frac{2}{10}\) + \(\frac{4}{10}\) + \(\frac{4}{10}\) = \(\frac{10}{10}\) = 1

Question 31. \(\frac{3}{10}\) + \(\frac{1}{10}\) + \(\frac{2}{10}\) = Answer: \(\frac{3}{10}\) + \(\frac{1}{10}\) + \(\frac{2}{10}\) = \(\frac{6}{10}\) = \(\frac{3}{5}\)

Question 32. \(\frac{4}{6}\) – \(\frac{2}{6}\) = Answer: \(\frac{4}{6}\) – \(\frac{2}{6}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\)

Question 33. \(\frac{3}{12}\) – \(\frac{2}{12}\) = Answer: \(\frac{3}{12}\) – \(\frac{2}{12}\) = \(\frac{1}{12}\)

Question 34. \(\frac{2}{3}\) + \(\frac{1}{3}\) = Answer: \(\frac{2}{3}\) + \(\frac{1}{3}\) = \(\frac{3}{3}\) = 1

Question 35. \(\frac{2}{4}\) + \(\frac{1}{4}\) = Answer: \(\frac{2}{4}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\)

Question 36. \(\frac{3}{12}\) + \(\frac{2}{12}\) = Answer: \(\frac{3}{12}\) + \(\frac{2}{12}\) = \(\frac{5}{12}\)

Question 37. \(\frac{1}{5}\) + \(\frac{2}{5}\) = Answer: \(\frac{1}{5}\) + \(\frac{2}{5}\) = \(\frac{3}{5}\)

Question 38. \(\frac{4}{5}\) – \(\frac{4}{5}\) = Answer: \(\frac{4}{5}\) – \(\frac{4}{5}\) = 0

Question 39. \(\frac{5}{12}\) – \(\frac{1}{12}\) = Answer: \(\frac{5}{12}\) – \(\frac{1}{12}\) = \(\frac{4}{12}\) = \(\frac{1}{3}\)

Question 40. \(\frac{6}{8}\) + \(\frac{2}{8}\) = Answer: \(\frac{6}{8}\) + \(\frac{2}{8}\) = \(\frac{8}{8}\) = 1

Question 41. \(\frac{2}{8}\) + \(\frac{2}{8}\) + \(\frac{2}{8}\) = Answer: \(\frac{2}{8}\) + \(\frac{2}{8}\) + \(\frac{2}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)

Question 42. \(\frac{9}{10}\) – \(\frac{7}{10}\) – \(\frac{1}{10}\) = Answer: \(\frac{9}{10}\) – \(\frac{7}{10}\) – \(\frac{1}{10}\) = \(\frac{9}{10}\) – \(\frac{8}{10}\) = \(\frac{1}{10}\) =

Question 43. \(\frac{2}{10}\) + \(\frac{5}{10}\) + \(\frac{2}{10}\) = Answer: \(\frac{2}{10}\) + \(\frac{5}{10}\) + \(\frac{2}{10}\) = \(\frac{9}{10}\)

Question 44. \(\frac{9}{12}\) – \(\frac{1}{12}\) – \(\frac{4}{12}\) = Answer: \(\frac{9}{12}\) – \(\frac{1}{12}\) – \(\frac{4}{12}\) = \(\frac{9}{12}\) – \(\frac{5}{12}\) = \(\frac{4}{12}\) = \(\frac{1}{3}\)  .

Eureka Math Grade 5 Module 3 Lesson 9 Problem Set Answer Key

Question 1. First make like units, and then add. a. \(\frac{3}{4}\) + \(\frac{1}{7}\) = b. \(\frac{1}{4}\) + \(\frac{9}{8}\) = c. \(\frac{3}{8}\) + \(\frac{3}{7}\) = d. \(\frac{4}{9}\) + \(\frac{4}{7}\) = e. \(\frac{1}{5}\) + \(\frac{2}{3}\) = f. \(\frac{3}{4}\) + \(\frac{5}{6}\) = g. \(\frac{2}{3}\) + \(\frac{1}{11}\) = h. \(\frac{3}{4}\) + 1\(\frac{1}{10}\) = Answer: a. \(\frac{3}{4}\) + \(\frac{1}{7}\) lcm of 4 and 7 is 28 =\(\frac{21}{28}\) + \(\frac{4}{28}\) = \(\frac{25}{28}\) b. \(\frac{1}{4}\) + \(\frac{9}{8}\) lcm of 4 and 8 is 8 \(\frac{2}{8}\) + \(\frac{9}{8}\) =\(\frac{11}{8}\) = 1\(\frac{3}{8}\) c. \(\frac{3}{8}\) + \(\frac{3}{7}\) lcm of 8 and 7 is 56 \(\frac{21}{56}\) + \(\frac{24}{56}\) = \(\frac{45}{56}\) d. \(\frac{4}{9}\) + \(\frac{4}{7}\) lcm of 9 and 7 is 63 \(\frac{28}{63}\) + \(\frac{36}{63}\) = \(\frac{64}{63}\) = 1\(\frac{1}{63}\) e. \(\frac{1}{5}\) + \(\frac{2}{3}\) lcm of 5 and 3 is 15 . \(\frac{3}{15}\) + \(\frac{10}{15}\) = \(\frac{13}{15}\) f. \(\frac{3}{4}\) + \(\frac{5}{6}\) lcm of 4 and 6 is 12. \(\frac{9}{12}\) + \(\frac{10}{12}\) = \(\frac{19}{12}\) =1 \(\frac{7}{12}\) g. \(\frac{2}{3}\) + \(\frac{1}{11}\) lcm of 3 and 11 is 33 \(\frac{22}{33}\) + \(\frac{3}{33}\) = \(\frac{25}{33}\) h. \(\frac{3}{4}\) + 1\(\frac{1}{10}\) = \(\frac{3}{4}\) + \(\frac{11}{10}\) lcm of 4 and 10 is 20. \(\frac{15}{20}\) + \(\frac{22}{10}\) = \(\frac{37}{20}\) = 1\(\frac{17}{20}\)

Question 2. Whitney says that to add fractions with different denominators, you always have to multiply the denominators to find the common unit; for example: \(\frac{1}{4}+\frac{1}{6}=\frac{6}{24}+\frac{4}{24}\) Show Whitney how she could have chosen a denominator smaller than 24, and solve the problem. Answer: multiples of 4 and 6 are 4 : 4, 8, 12, 16, 20, 24 6: 6, 12, 18, 24, 30 . 12 and 24 are the common multiplies of 4 and 6. smaller than 24 we get 12 multiple . (\(\frac{1 × 3}{4 × 3}\)) + (\(\frac{1 × 2}{6 × 2}\)) = \(\frac{3}{12}\) + \(\frac{2}{12}\) = \(\frac{5}{12}\)

Question 3. Jackie brought \(\frac{3}{4}\) of a gallon of iced tea to the party. Bill brought \(\frac{7}{8}\) of a gallon of iced tea to the same party. How much iced tea did Jackie and Bill bring to the party? Answer: Fraction of iced tea brought by Jackie = \(\frac{3}{4}\) Fraction of iced tea brought by Bill = \(\frac{7}{8}\) Total Fraction of iced tea brought to party = \(\frac{3}{4}\) + \(\frac{7}{8}\)  = \(\frac{6}{8}\) + \(\frac{7}{8}\) = \(\frac{13}{8}\) = 1\(\frac{5}{8}\) Therefore, Total Fraction of iced tea brought to party = \(\frac{13}{8}\) = 1\(\frac{5}{8}\) .

Question 4. Madame Curie made some radium in her lab. She used \(\frac{2}{5}\) kg of the radium in an experiment and had 1\(\frac{1}{4}\) kg left. How much radium did she have at first? (Extension: If she performed the experiment twice, how much radium would she have left?) Answer: Quantity of Radium made by Madam Curie = x kgs Fraction of Quantity of Radium used by Experiment = \(\frac{2}{5}\) kg Fraction of Quantity of Radium left = 1\(\frac{1}{4}\) kg = \(\frac{5}{4}\) kg Quantity of Radium made by Madam Curie = \(\frac{2}{5}\) + \(\frac{5}{4}[/latex lcm of 5 and 4 is 20 . [latex]\frac{8}{20}\)  + \(\frac{25}{20}\) = \(\frac{33}{20}\) =1\(\frac{13}{20}\) . Therefore if the experiment is done once the Total Quantity = \(\frac{33}{20}\) =1\(\frac{13}{20}\) If the Experiment if done twiced . Total Quantity – Quantity Used for Experiment twice = left Quantity . \(\frac{33}{20}\) – 2 × \(\frac{2}{5}\) = \(\frac{33}{20}\) –  \(\frac{4}{5}\) = \(\frac{33}{20}\) – \(\frac{16}{20}\) = \(\frac{17}{20}\) Therefore if the experiment is done once the Total Quantity = \(\frac{17}{20}\)

Eureka Math Grade 5 Module 3 Lesson 9 Exit Ticket Answer Key

Make like units, and then add. a. \(\frac{1}{6}\) + \(\frac{3}{4}\) = b. 1\(\frac{1}{2}\) + \(\frac{2}{5}\) = Answer: a. \(\frac{1}{6}\) + \(\frac{3}{4}\) lcm of 6 and 4 is 12 \(\frac{2}{12}\) + \(\frac{9}{12}\) = \(\frac{11}{12}\) b. 1\(\frac{1}{2}\) + \(\frac{2}{5}\) = \(\frac{3}{2}\) + \(\frac{2}{5}\) lcm of 2 and 5 is 10. \(\frac{15}{10}\) + \(\frac{4}{10}\) =\(\frac{19}{10}\) = 1\(\frac{9}{10}\)

Eureka Math Grade 5 Module 3 Lesson 9 Homework Answer Key

Question 1. Make like units, and then add. a. \(\frac{3}{5}\) + \(\frac{1}{3}\) = b. \(\frac{3}{5}\) + \(\frac{1}{11}\) = c. \(\frac{2}{9}\) + \(\frac{5}{6}\) = d. \(\frac{2}{5}\) + \(\frac{1}{4}\) + \(\frac{1}{10}\) = e. \(\frac{1}{3}\) + \(\frac{7}{5}\) = f. \(\frac{5}{8}\) + \(\frac{7}{12}\) = g. 1\(\frac{1}{3}\) + \(\frac{3}{4}\) = h. \(\frac{5}{6}\) + 1\(\frac{1}{4}\) = Answer: a. \(\frac{3}{5}\) + \(\frac{1}{3}\) lcm of 5 and 3 is 15 \(\frac{9}{15}\) + \(\frac{5}{15}\) = \(\frac{14}{15}\) b. \(\frac{3}{5}\) + \(\frac{1}{11}\) lcm of 5 and 11 is 55 \(\frac{33}{55}\) + \(\frac{5}{55}\) = \(\frac{38}{55}\) c. \(\frac{2}{9}\) + \(\frac{5}{6}\) lcm of 9 and 6 is 18 . \(\frac{4}{18}\) + \(\frac{15}{18}\) = \(\frac{19}{18}\) = 1 \(\frac{1}{18}\) d. \(\frac{2}{5}\) + \(\frac{1}{4}\) + \(\frac{1}{10}\) lcm of 5 , 4 and 10 is 20 . \(\frac{8}{20}\) + \(\frac{5}{20}\) + \(\frac{2}{20}\) = \(\frac{15}{20}\)= \(\frac{3}{4}\) e. \(\frac{1}{3}\) + \(\frac{7}{5}\) lcm of 3 and 5 is 15 . \(\frac{5}{15}\) + \(\frac{21}{15}\) =\(\frac{26}{3}\) =1\(\frac{11}{15}\) f. \(\frac{5}{8}\) + \(\frac{7}{12}\) lcm of 8 and 12 is 24. \(\frac{15}{24}\) + \(\frac{14}{24}\) = \(\frac{29}{24}\) = 1\(\frac{5}{24}\) g. 1\(\frac{1}{3}\) + \(\frac{3}{4}\) = \(\frac{4}{3}\) + \(\frac{3}{4}\) lcm of 3 and 4  is 12 \(\frac{16}{12}\) + \(\frac{9}{12}\) = \(\frac{25}{12}\) = 2 \(\frac{1}{12}\) h. \(\frac{5}{6}\) + 1\(\frac{1}{4}\) =\(\frac{5}{6}\) + \(\frac{5}{4}\) lcm of 4 and 6 is 12 . \(\frac{10}{12}\) + \(\frac{15}{12}\) = \(\frac{25}{12}\) = 2\(\frac{1}{12}\)

Question 2. On Monday, Ka practiced guitar for \(\frac{2}{3}\) of one hour. When she finished, she practiced piano for \(\frac{3}{4}\) of one hour. How much time did Ka spend practicing instruments on Monday? Answer: Fraction of Time spent in playing guitar of one hour = \(\frac{2}{3}\) Fraction of Time spent in playing guitar when finished = \(\frac{3}{4}\) Total Time taken for practicing = \(\frac{2}{3}\) + \(\frac{3}{4}\) = \(\frac{8}{12}\) + \(\frac{9}{12}\) = \(\frac{17}{12}\) = 1\(\frac{5}{12}\) hour . Therefore, Total Time taken in practicing = \(\frac{17}{12}\) = 1\(\frac{5}{12}\) hour

Question 3. Ms. How bought a bag of rice for dinner. She used \(\frac{3}{5}\) kg of the rice and still had 2\(\frac{1}{4}\) kg left. How heavy was the bag of rice that Ms. How bought? Answer: Fraction of Quantity of rice used = \(\frac{3}{5}\) kg Fraction of Quantity of rice left = 2\(\frac{1}{4}\) kg Total Quantity of rice = \(\frac{3}{5}\)  + 2\(\frac{1}{4}\)  = \(\frac{3}{5}\) + \(\frac{9}{4}\) = \(\frac{12}{20}\) + \(\frac{45}{20}\) =\(\frac{57}{20}\) = 2\(\frac{17}{20}\) Therefore, Total Quantity of rice = \(\frac{57}{20}\) = 2\(\frac{17}{20}\) .

Question 4. Joe spends \(\frac{2}{5}\) of his money on a jacket and \(\frac{3}{8}\) of his money on a shirt. He spends the rest on a pair of pants. What fraction of his money does he use to buy the pants? Answer: Money spent on jacket = \(\frac{2}{5}\) Money spent on a shirt = \(\frac{3}{8}\) Money spent on pair of pants = x 1 = \(\frac{2}{5}\) + \(\frac{3}{8}\)  + x lcm of 5 and 8 is 40. \(\frac{40}{40}\)  = \(\frac{16}{40}\) + \(\frac{10}{40}\) +x \(\frac{40}{40}\)  = \(\frac{26}{40}\) + x x = \(\frac{40}{40}\)  – \(\frac{13}{40}\) x = \(\frac{27}{40}\)

Leave a Comment Cancel Reply

You must be logged in to post a comment.