critical thinking process mathematics

Check Out the New Website Shop!

Novels & Picture Books

Anchor Charts

• Critical Thinking

How To Encourage Critical Thinking in Math

By Mary Montero

Share This Post:

• Facebook Share
• Twitter Share
• Pinterest Share
• Email Share

Critical thinking is more than just a buzzword… It’s an essential skill that helps students develop problem-solving abilities and make logical connections between different concepts. By encouraging critical thinking in math, students learn to approach problems more thoughtfully, they learn to analyze and evaluate math concepts, identify patterns and relationships, and explore different strategies for finding the solution. Critical thinking also involves a great deal of persistence. Those are critical life skills!

When you think about it, students are typically asked to solve math problems and find the answer. Showing their work is frequently stressed too, which is important, but not the end. Instead, students need to be able to look at math in different ways in order to truly grasp a complete understanding of math concepts. Mathematics requires logical reasoning, problem-solving, and abstract thinking.

What Does Critical Thinking in Math Look Like?

When I think about critical thinking in math, I focus on:

• Solving problems through logical thinking . Students learn how to break down complex problems, analyze the different parts, and understand how they fit together logically.
• Identifying patterns and making connections. Students learn how to identify patterns across different math concepts, make connections between seemingly unrelated topics, and develop a more in-depth understanding of how math works.
• Evaluating and comparing solutions. Students learn to evaluate which solution is best for a given problem and identify any flaws in their reasoning or others’ reasoning when looking at different solutions

Mathematician Posters

These FREE Marvelous Mathematician posters have been a staple in my classroom for the last 8+ years! I first started using a version from MissMathDork and adapted them for my classroom over the years. 

I print, laminate, and add magnetic stickers on the back. At the beginning of the year, I only put one or two up at a time depending on our area of focus. Now, they are all hanging on my board, and I’ll pull out different ones depending on our area of focus. They are so empowering to my mathematicians and help them stay on track!

A Marvelous Mathematician:

• knows that quicker doesn’t mean better
• looks for patterns
• knows mistakes happen and keeps going
• makes sense of the most important details
• embraces challenges and works through frustrations
• uses proper math vocabulary to explain their thinking
• shows their work and models their thinking
• discusses solutions and evaluates reasonableness
• gives context by labeling answers
• applies mathematical knowledge to similar situations
• checks for errors (computational and conceptual)

Critical Thinking Math Activities

Here are a few of my favorite critical thinking activities. 

Square Of Numbers

I love to incorporate challenge problems (use Nrich and Openmiddle to get started) because they teach my students so much more than how to solve a math problem. They learn important lessons in teamwork, persistence, resiliency, and growth mindset. We talk about strategies for tackling difficult problems and the importance of not giving up when things get hard.

This square of numbers challenge was a hit!

ALL kids need to feel and learn to embrace challenge. Oftentimes, kids I see have rarely faced an academic challenge. Things have just come easy to them, so when it doesn’t, they can lack strategies that will help them. In fact, they will often give up before they even get started.

I tell them it’s my job to make sure I’m helping them stretch and grow their brain by giving them challenges. They don’t love it at first, but they eventually do! 

This domino challenge was another one from Nrich . I’m always on the hunt for problems like this!!  How would you guide students toward an answer??

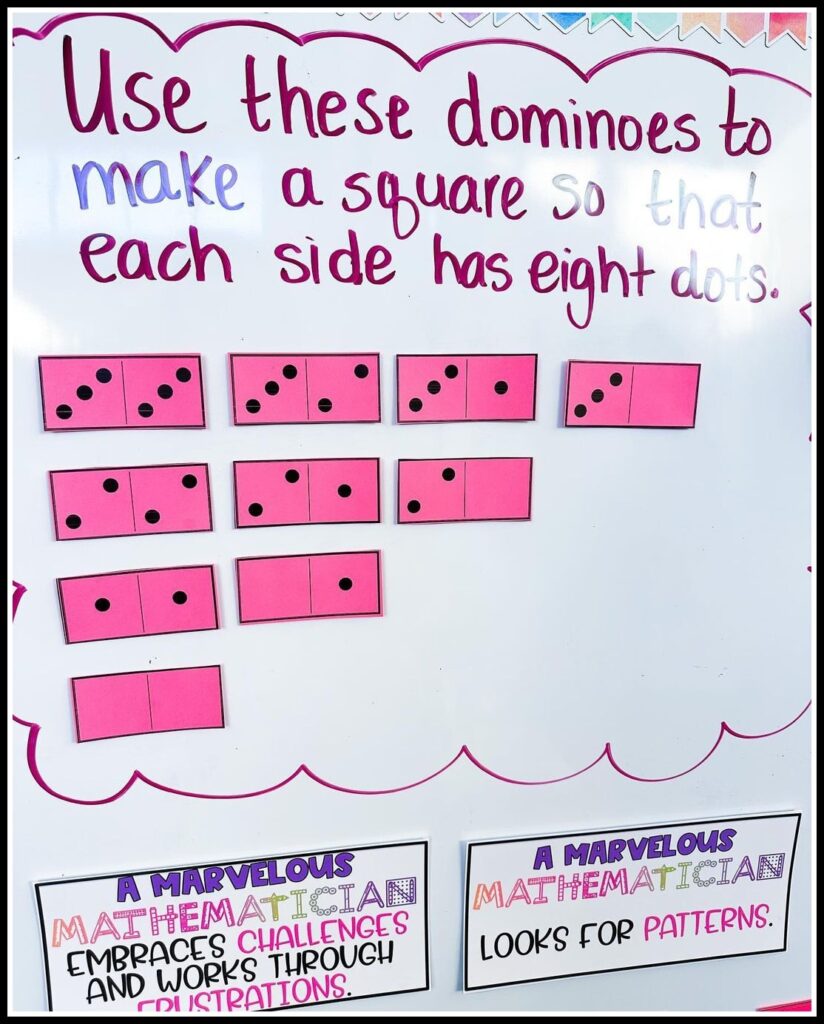
Fifteen Cards

This is a well-loved math puzzle with my students, and it’s amazing for encouraging students to consider all options when solving a math problem.

We have number cards 1-15 (one of each number) and only seven are laid out. With the given clues, students need to figure out which seven cards should be put out and in what order. My students love these, and after they’ve done a few, they enjoy creating their own, too! Use products, differences, and quotients to increase the challenge.

This is also adapted from Nrich, which is an AMAZING resource for math enrichment!

This is one of my favorite fraction lessons that I’ve done for years! Huge shout out to Meg from The Teacher Studio for this one. I give each child a slip of paper with this figure and they have to silently write their answer and justification. Then I tally up the answers and have students take a side and DEBATE with their reasoning! It’s an AMAZING conversation, and I highly recommend trying it with your students. 

Sometimes we leave it hanging overnight and work on visual models to make some proofs. 

Logic Puzzles

Logic puzzles are always a hit too! You can enrich and extend your math lessons with these ‘Math Mystery’ logic puzzles that are the perfect challenge for 4th, 5th, and 6th grades. The puzzles are skills-based, so they integrate well with almost ANY math lesson. You can use them to supplement instruction or challenge your fast-finishers and gifted students… all while encouraging critical thinking about important math skills!

Three levels are included, so they’re perfect to use for differentiation.

• Introductory logic puzzles are great for beginners (4th grade and up!)
• Advanced logic puzzles are great for students needing an extra challenge
• Extra Advanced logic puzzles are perfect for expert solvers… we dare you to figure these puzzles out! 

Do you have a group of students who are ready for more of a fraction challenge? My well-loved fraction puzzlers are absolutely perfect for fraction enrichment. They’ll motivate your students to excel at even the most challenging tasks! 

Math Projects

Math projects are another way to differentiation while building critical thinking skills. Math projects hold so much learning power with their real-world connections, differentiation options, collaborative learning opportunities, and numerous avenues for cross curricular learning too. 

If you’re new to math projects, I shared my best tips and tricks for using math projects in this blog post . They’re perfect for cumulative review, seasonal practice, centers, early finisher work, and more.

I use both concept-based math projects to focus on specific standards and seasonal math projects that integrate several skills.

Error Analysis

Finally, error analysis is always a challenging way to encourage critical thinking. When we use error analysis, we encourage students to analyze their own mistakes to prevent making the same mistakes in the future.

For my gifted students, I use error analysis tasks as an assessment when they have shown mastery of a unit during other tasks. For students in the regular classroom needing enrichment, I usually have them complete the tasks in a center or with a partner.

For students needing extra support, we complete error analysis in small groups.  We go step-by-step through the concept and they are always able to eventually identify what the error is. It is so empowering to students when they finally figure out the error AND it helps prevent them from making the same error in the future!

My FREE addition error analysis is a good place to start, no matter the grade level. I show them the process of walking through the problem and how best to complete an error analysis task.

When you’re ready for more, this bundle of error analysis tasks contains more than 240 tasks to engage and enrich your students in critical thinking practice.

If you want to dig even deeper, visit this conceptual vs computational error analysis post to learn more about using error analysis in the classroom. 

Related Critical Thinking Posts

• How to Increase Critical Thinking and Creativity in Your “Spare” Time
• More Tips to Increase Critical Thinking

Critical thinking is essential for students to develop a deeper understanding of math concepts, problem-solving skills, and a stronger ability to reason logically. When you learn how to encourage critical thinking in math, you’re setting your students up for success not only in more advanced math subjects they’ll encounter, but also in life. 

How do you integrate critical thinking in your classroom? Come share your ideas with us in our FREE Inspired In Upper Elementary Facebook group .

Mary Montero

I’m so glad you are here. I’m a current gifted and talented teacher in a small town in Colorado, and I’ve been in education since 2009. My passion (other than my family and cookies) is for making teachers’ lives easier and classrooms more engaging.

You might also like…

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

One Comment

Mary Thankyou for your inspirational activities. I have just read and loved the morning talk activities. I do have meetings with my students but usually at end of day. What time do you

©2023 Teaching With a Mountain View . All Rights Reserved | Designed by Ashley Hughes

Username or Email Address

Remember Me

Lost your password?

Review Cart

No products in the cart.

How to Improve Problem-Solving Skills: Mathematics and Critical Thinking

In today’s rapidly changing world, problem-solving has become a quintessential skill. When we discuss the topic, it’s natural to ask, “What is problem-solving?” and “How can we enhance this skill, particularly in children?” The discipline of mathematics offers a rich platform to explore these questions. Through math, not only do we delve into numbers and equations, but we also explore how to improve problem-solving skills and how to develop critical thinking skills in math. Let’s embark on this enlightening journey together.

What is Problem-Solving?

At its core, problem-solving involves identifying a challenge and finding a solution. But it’s not always as straightforward as it sounds. So, what is problem-solving? True problem-solving requires a combination of creative thinking and logical reasoning. Mathematics, in many ways, embodies this blend. When a student approaches a math problem, they must discern the issue at hand, consider various methods to tackle it, and then systematically execute their chosen strategy.

But what is problem-solving in a broader context? It’s a life skill. Whether we’re deciding the best route to a destination, determining how to save for a big purchase, or even figuring out how to fix a broken appliance, we’re using problem-solving.

How to Develop Critical Thinking Skills in Math

Critical thinking goes hand in hand with problem-solving. But exactly how to develop critical thinking skills in math might not be immediately obvious. Here are a few strategies:

• Contextual Learning: Teaching math within a story or real-life scenario makes it relevant. When students see math as a tool to navigate the world around them, they naturally begin to think critically about solutions.
• Open-ended Questions: Instead of merely seeking the “right” answer, encourage students to explain their thought processes. This nudges them to think deeply about their approach.
• Group Discussions: Collaborative learning can foster different perspectives, prompting students to consider multiple ways to solve a problem.
• Challenging Problems: Occasionally introducing problems that are a bit beyond a student’s current skill level can stimulate critical thinking. They will have to stretch their understanding and think outside the box.

What are the Six Basic Steps of the Problem-Solving Process?

Understanding how to improve problem-solving skills often comes down to familiarizing oneself with the systematic approach to challenges. So, what are the six basic steps of the problem-solving process?

• Identification: Recognize and define the problem.
• Analysis: Understand the problem’s intricacies and nuances.
• Generation of Alternatives: Think of different ways to approach the challenge.
• Decision Making: Choose the most suitable method to address the problem.
• Implementation: Put the chosen solution into action.
• Evaluation: Reflect on the solution’s effectiveness and learn from the outcome.

By embedding these steps into mathematical education, we provide students with a structured framework. When they wonder about how to improve problem-solving skills or how to develop critical thinking skills in math, they can revert to this process, refining their approach with each new challenge.

Making Math Fun and Relevant

At Wonder Math, we believe that the key to developing robust problem-solving skills lies in making math enjoyable and pertinent. When students see math not just as numbers on a page but as a captivating story or a real-world problem to be solved, their engagement skyrockets. And with heightened engagement comes enhanced understanding.

As educators and parents, it’s crucial to continuously ask ourselves: how can we demonstrate to our children what problem-solving is? How can we best teach them how to develop critical thinking skills in math? And how can we instill in them an understanding of the six basic steps of the problem-solving process?

The answer, we believe, lies in active learning, contextual teaching, and a genuine passion for the beauty of mathematics.

The Underlying Beauty of Mathematics

Often, people perceive mathematics as a rigid discipline confined to numbers and formulas. However, this is a limited view. Math, in essence, is a language that describes patterns, relationships, and structures. It’s a medium through which we can communicate complex ideas, describe our universe, and solve intricate problems. Understanding this deeper beauty of math can further emphasize how to develop critical thinking skills in math.

Why Mathematics is the Ideal Playground for Problem-Solving

Math provides endless opportunities for problem-solving. From basic arithmetic puzzles to advanced calculus challenges, every math problem offers a chance to hone our problem-solving skills. But why is mathematics so effective in this regard?

• Structured Challenges: Mathematics presents problems in a structured manner, allowing learners to systematically break them down. This format mimics real-world scenarios where understanding the structure of a challenge can be half the battle.
• Multiple Approaches: Most math problems can be approached in various ways . This teaches learners flexibility in thinking and the ability to view a single issue from multiple angles.
• Immediate Feedback: Unlike many real-world problems where solutions might take time to show results, in math, students often get immediate feedback. They can quickly gauge if their approach works or if they need to rethink their strategy.

Enhancing the Learning Environment

To genuinely harness the power of mathematics in developing problem-solving skills, the learning environment plays a crucial role. A student who is afraid of making mistakes will hesitate to try out different approaches, stunting their critical thinking growth.

However, in a nurturing, supportive environment where mistakes are seen as learning opportunities, students thrive. They become more willing to take risks, try unconventional solutions, and learn from missteps. This mindset, where failure is not feared but embraced as a part of the learning journey, is pivotal for developing robust problem-solving skills.

Incorporating Technology

In our digital age, technology offers innovative ways to explore math. Interactive apps and online platforms can provide dynamic problem-solving scenarios, making the process even more engaging. These tools can simulate real-world challenges, allowing students to apply their math skills in diverse contexts, further answering the question of how to improve problem-solving skills.

More than Numbers 

In summary, mathematics is more than just numbers and formulas—it’s a world filled with challenges, patterns, and beauty. By understanding its depth and leveraging its structured nature, we can provide learners with the perfect platform to develop critical thinking and problem-solving skills. The key lies in blending traditional techniques with modern tools, creating a holistic learning environment that fosters growth, curiosity, and a lifelong love for learning.

Join us on this transformative journey at Wonder Math. Let’s make math an adventure, teaching our children not just numbers and equations, but also how to improve problem-solving skills and navigate the world with confidence. Enroll your child today and witness the magic of mathematics unfold before your eyes!

FAQ: Mathematics and Critical Thinking

1. what is problem-solving in the context of mathematics.

Problem-solving in mathematics refers to the process of identifying a mathematical challenge and systematically working through methods and strategies to find a solution.

2. Why is math considered a good avenue for developing problem-solving skills?

Mathematics provides structured challenges and allows for multiple approaches to find solutions. This promotes flexibility in thinking and encourages learners to view problems from various angles.

3. How does contextual learning enhance problem-solving abilities?

By teaching math within a story or real-life scenario, it becomes more relevant for the learner. This helps them see math as a tool to navigate real-world challenges , thereby promoting critical thinking.

4. What are the six basic steps of the problem-solving process in math?

The six steps are: Identification, Analysis, Generation of Alternatives, Decision Making, Implementation, and Evaluation.

5. How can parents support their children in developing mathematical problem-solving skills?

Parents can provide real-life contexts for math problems , encourage open discussions about different methods, and ensure a supportive environment where mistakes are seen as learning opportunities.

6. Are there any tools or apps that can help in enhancing problem-solving skills in math?

Yes, there are various interactive apps and online platforms designed specifically for math learning. These tools provide dynamic problem-solving scenarios and simulate real-world challenges, making the learning process engaging.

7. How does group discussion foster critical thinking in math?

Group discussions allow students to hear different perspectives and approaches to a problem. This can challenge their own understanding and push them to think about alternative methods.

8. Is it necessary to always follow the six steps of the problem-solving process sequentially?

While the six steps provide a structured approach, real-life problem-solving can sometimes be more fluid. It’s beneficial to know the steps, but adaptability and responsiveness to the situation are also crucial.

9. How does Wonder Math incorporate active learning in teaching mathematics?

Wonder Math integrates mathematics within engaging stories and real-world scenarios, making it fun and relevant. This active learning approach ensures that students are not just passive recipients but active participants in the learning process.

10. What if my child finds a math problem too challenging and becomes demotivated?

It’s essential to create a supportive environment where challenges are seen as growth opportunities. Remind them that every problem is a chance to learn, and it’s okay to seek help or approach it differently.

Related posts

Summer Math Programs: How They Can Prevent Learning Loss in Young Students

As summer approaches, parents and educators alike turn their attention to how they can support young learners during the break. Summer is a time for relaxation, fun, and travel, yet it’s also a critical period when learning loss can occur. This phenomenon, often referred to as the “summer slide,” impacts students’ progress, especially in foundational subjects like mathematics. It’s reported…

Math Programs 101: What Every Parent Should Know When Looking For A Math Program

  As a parent, you know that a solid foundation in mathematics is crucial for your child’s success, both in school and in life. But with so many math programs and math help services out there, how do you choose the right one? Whether you’re considering Outschool classes, searching for “math tutoring near me,” or exploring tutoring services online, understanding…

Engaging Maths

Promoting creative and critical thinking in mathematics and numeracy.

What is critical and creative thinking, and why is it so important in mathematics and numeracy education?

Numeracy is often defined as the ability to apply mathematics in the context of day to day life. However, the term ‘critical numeracy’ implies much more. One of the most basic reasons for learning mathematics is to be able to apply mathematical skills and knowledge to solve both simple and complex problems, and, more than just allowing us to navigate our lives through a mathematical lens, being numerate allows us to make our world a better place.

The mathematics curriculum in Australia provides teachers with the perfect opportunity to teach mathematics through critical and creative thinking. In fact, it’s mandated. Consider the core processes of the curriculum. The Australian Curriculum (ACARA, 2017), requires teachers to address four proficiencies : Problem Solving, Reasoning, Fluency, and Understanding. Problem solving and reasoning require critical and creative thinking (). This requirement is emphasised more heavily in New South wales, through the graphical representation of the mathematics syllabus content , which strategically places Working Mathematically (the proficiencies in NSW) and problem solving, at its core. Alongside the mathematics curriculum, we also have the General Capabilities , one of which is Critical and Creative Thinking – there’s no excuse!

Critical and creative thinking need to be embedded in every mathematics lesson . Why? When we embed critical and creative thinking, we transform learning from disjointed, memorisation of facts, to sense-making mathematics. Learning becomes more meaningful and purposeful for students.

How and when do we embed critical and creative thinking?

There are many tools and many methods of promoting thinking. Using a range of problem solving activities is a good place to start, but you might want to also use some shorter activities and some extended activities. Open-ended tasks are easy to implement, allow all learners the opportunity to achieve success, and allow for critical thinking and creativity. Tools such as Bloom’s Taxonomy and Thinkers Keys  are also very worthwhile tasks. For good mathematical problems go to the nrich website . For more extended mathematical investigations and a wonderful array of rich tasks, my favourite resource is Maths300   (this is subscription based, but well worth the money). All of the above activities can be used in class and/or for homework, as lesson starters or within the body of a lesson.

Will critical and creative thinking take time away from teaching basic concepts?

No, we need to teach mathematics in a way that has meaning and relevance, rather than through isolated topics. Therefore, teaching through problem-solving rather than for problem-solving. A classroom that promotes and critical and creative thinking provides opportunities for:

• higher-level thinking within authentic and meaningful contexts;
• complex problem solving;
• open-ended responses; and
• substantive dialogue and interaction.

Who should be engaging in critical and creative thinking?

Is it just for students? No! There are lots of reasons that teachers should be engaged with critical and creative thinking. First, it’s important that we model this type of thinking for our students. Often students see mathematics as black or white, right or wrong. They need to learn to question, to be critical, and to be creative. They need to feel they have permission to engage in exploration and investigation. They need to move from consumers to producers of mathematics.

Secondly, teachers need to think critically and creatively about their practice as teachers of mathematics. We need to be reflective practitioners who constantly evaluate our work, questioning curriculum and practice, including assessment, student grouping, the use of technology, and our beliefs of how children best learn mathematics.

Critical and creative thinking is something we cannot ignore if we want our students to be prepared for a workforce and world that is constantly changing. Not only does it equip then for the future, it promotes higher levels of student engagement, and makes mathematics more relevant and meaningful.

How will you and your students engage in critical and creative thinking?

Share this:

[…] of this recognition that the 1940s menu makes a perfect stimulus for mathematical investigation and critical thinking. The links between mathematics and children’s lives are not always obvious for students, so […]

[…] several of my previous posts I discussed the importance of promoting critical thinking in mathematics teaching and learning. I’ve also discussed at length various ways to contextualise […]

Leave a comment Cancel reply

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar

We apologize for the inconvenience...

To ensure we keep this website safe, please can you confirm you are a human by ticking the box below.

If you are unable to complete the above request please contact us using the below link, providing a screenshot of your experience.

https://ioppublishing.org/contacts/

Conceptualising critical mathematical thinking in young students

• Original Article
• Open access
• Published: 08 February 2023
• Volume 35 , pages 339–359, ( 2023 )

Cite this article

You have full access to this open access article

• Chrissy Monteleone   ORCID: orcid.org/0000-0002-3860-2109 1 ,
• Jodie Miller   ORCID: orcid.org/0000-0003-0561-9972 2 &
• Elizabeth Warren 2  

5325 Accesses

4 Citations

3 Altmetric

Explore all metrics

International curriculum and policy directions have called to embed critical thinking across discipline areas including mathematics; however, conceptually, this is under-theorised and under-researched in the field of mathematics education. This paper presents the conceptualisation of critical mathematical thinking (CMT) and the application of a literature informed conceptual framework; in particular, it examines what CMT capabilities young students exhibit as they enter formal schooling. We present the findings from one-on-one task-based interviews, undertaken with 16 young students (aged 5–6) as a means to investigate their CMT capabilities and refine the CMT framework. The interview data were analysed using the new critical mathematical thinking conceptual framework. The data confirms the definition and understanding of CMT in young students, indicating a need for curriculum refinement, improved teaching practices, and further research in this area.

Similar content being viewed by others

Threshold Concepts in Primary School Maths and Science: An Investigation of Some Underlying Ideas of STEM

Mapping Computational Thinking Skills to the South African Secondary School Mathematics Curriculum

Critical stance within a community of inquiry in an advanced mathematics course for pre-service teachers

Avoid common mistakes on your manuscript.

Introduction

Internationally, curriculum expectations indicate that as young students progress through primary school, they need to build capabilities in both critical thinking and mathematical thinking. In Australia, the term critical thinking is referred to in both the Australian National Curriculum (ACARA, 2014 ) and the Early Years Learning Framework (DEEWR,  2022 ) with an expectation that learning experiences are provided to support young students to develop this thinking from before school settings through to the end of primary school across a range of disciplines (Ab Kadir, 2018 ; Heard et al., 2020 ). As such, critical thinking is not seen as discipline specific but rather a general capability that is embedded in all subject areas, including mathematics.

Critical thinking is found to be a necessary requirement in both education and employability (Heard et al., 2020 ; National Council of Teachers of Mathematics (NCTM), 2000a ,  b ; Urib-Enciso et al., 2017 ). Critical thinking is defined as process skills, qualities, competencies and characteristics that help individuals to analyse a situation and make judgements (Elder & Paul, 2020 ; Lai, 2011 ; Lipman, 1987 ; Siswono, 2010 ; Sternberg, 1986 ). Internationally, curriculum and policy directions have embedded critical thinking as a key skill to support students to become prepared for the twenty-first century (Urib-Enciso et al., 2017 ). In addition, research evidences that twenty-first-century skills that are underpinned by critical thinking are required for workforce preparedness and long-term economic success (Burrus et al., 2013 ; Rios et al., 2020 ). Despite this, presently, there is little understanding of how critical thinking presents in young students.

Mathematics is a required subject area across levels of education. It can be defined as knowledge, skills, understandings and procedures that require an individual to interpret mathematical content of patterns, like number and space (Animasaun, 2021 ).Curriculum documents internationally and locally identify the necessity of mathematics for teaching and the need to acquire  mathematical thinking processes. However, the embedding of mathematical thinking as a theme in curriculum documents varies. For example, the American National Council of Teachers of Mathematics (Ferrini-Mundy, 2000 ) includes the processes of problem solving, reasoning and proof, communication, connections and representations, whereas the Singaporean Mathematics Framework identifies five areas of mathematical proficiency. These are conceptual understanding, procedural fluency, strategic competence, adaptive reasoning and productive disposition (Groves, 2012 ). The Australian Curriculum: Mathematics includes the following proficiency (process) strands: understanding, fluency, problem solving and reasoning, which are at the centre of the curriculum.

Mathematical thinking is deemed an important construct that underpins one’s ability to solve problems; however, Australian students continue to underperform in both international and national mathematical benchmarks. In comparison to other countries, Australian students’ mathematical performance has at best plateaued and in some cases has declined over recent years (McGaw et al., 2020 ; Thomson et al., 2020 ). This decline is particularly prevalent in the area of mathematical thinking with Australian students underperforming in the cognitive domains of knowing and applying; however, data suggests an increase in Australian students reasoning ability in the Trends in International Mathematics and Science Study (TIMSS) (Thomson et al., 2020 ). Thus, overall, Year 4 students have demonstrated no change in their mathematics achievement in TIMSS between 2015 and 2019, with 70% attaining national proficiency standards which is less than the international medium (Thomson et al., 2020 ). While mathematical thinking appears to contribute to the decline in mathematics performance, we argue in this paper that there are also implications for that application of critical thinking in this discipline area. The two types of thinking, critical and mathematical, need to be more closely considered in mathematics, with strong foundations formed early in a child’s schooling.

While there is considerable research that supports that many young students are mathematically competent prior to entering formal schooling (Clarke et al., 2006 ; Clements & Sarama, 2011 ; Hunting et al., 2009 ; MacDonald & Carmichael, 2018 ; Papic & Mulligan, 2005 ; Perry et al., 2015 ; Scammacca et al., 2020 ) and mathematical thinking begins at a young age (Bobis et al., 2005 ; Doig & Ompok, 2010 ; Sarama & Clements, 2009 ), there is little understanding between the relationship of mathematical thinking and critical thinking for young learners. There are a number of inconsistencies in and overlaps between both critical thinking and mathematical thinking definitions in the research literature and curriculum documents. In this paper, we address this gap by drawing on the research literature pertaining to critical thinking and mathematical thinking to conceptualise and define the term critical mathematical thinking (CMT). This new term (CMT) is then further conceptualised to present the critical mathematical thinking conceptual framework, presented in the following sections. Data presented in this paper is analysed in light of the critical mathematical thinking conceptual framework to provide evidence of the types of critical mathematical thinking young students displayed as they entered formal schooling. These data support the final reconceptualization of the framework to present the critical mathematical thinking framework for young students.

Conceptualising critical mathematical thinking

For the larger study, a review of the seminal literature pertaining to the broad areas of critical thinking and mathematical thinking was conducted (Monteleone, 2021 ). The review of both sets of literature provided an opportunity to blend critical and mathematical thinking to establish an initial literature informed conceptual framework for defining critical mathematical thinking. It is important to note that in this context, critical mathematical thinking is not a term pertaining to critical mathematical education or mathematics for social justice (Skovsmose, 1994 ), but is a focus on applying critical thinking within a mathematical context. The following sections present the analysis of the themes (overarching recurring terms) and sub-themes (secondary terms aligned to the overarching theme) that emerged across the critical thinking and mathematical thinking literature to develop an initial conceptual framework of critical mathematical thinking.

Themes pertaining to critical thinking

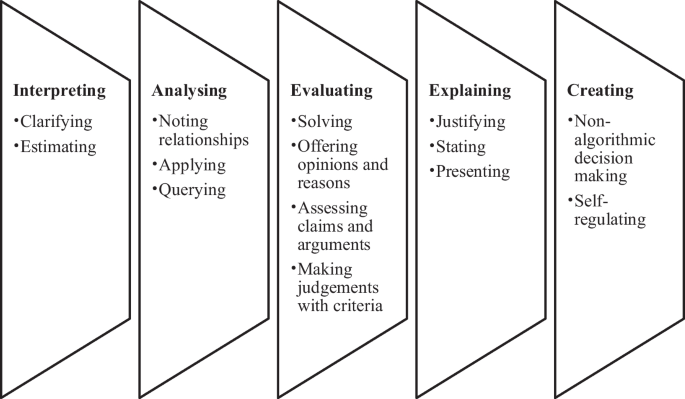
The term, critical thinking , has been explored by many researchers, for example, Davies ( 2006 ), Ennis ( 1992 ), and Facione ( 1990 ), and primarily within the “critical thinking movement” in the USA. The definition is complicated as critical thinking often encapsulates: a judgement; a sceptical and interim view of knowledge, a simple innovation, a way to make sense of texts; rationality, the adoption of an ethical and activist stance and self-reflexivity (Moore, 2013 ). Since the early critical thinking movement, research in this space has primarily focused on skills, qualities, competencies and characteristics of individuals across a range of disciplines including philosophy, psychology and education (Heard et al., 2020 ). Siswono ( 2010 , p. 19) states that, “critical thinking is thinking that examines, relates, and evaluates all aspects of a situation or problem”. While there is no consensus on terms used to define critical thinking, it is apparent that there are five recurring themes referred to in the literature describing the cognitive skills or dispositions to represent critical thinking. These five themes are (i) interpreting, (ii) analysing, (iii) evaluating, (iv) explaining and (v) creating. Additionally, when examining the literature, it appeared that the themes were not hierarchical in nature. The following examines these five themes pertaining to critical thinking.

Interpreting

Critical thinking experts include interpreting as a key indicator of critical thinking ability (Ellerton, 2018 ; Ennis, 2013 ; Facione & Facione, 2008 ; Watson & Glaser, 2002 ). According to Watson and Glaser ( 2002 ), interpreting is when an individual can form a logical judgement about conclusions generated. Facione ( 2011 ) states that ideal critical thinkers make decisions, which can result in interpretation. To further position how a critical thinker uses the skill of interpreting, the literature reviewed elaborates on interpreting to include sub-themes of assessing (Facione, 2011 ), categorising (Ellerton, 2018 ; Facione, 2011 ), decoding (Facione, 2011 ), clarifying (Facione, 2011 ) and identifying (Facione, 2011 ). The seminal work of Lipman ( 1987 ) provided associated sub-themes for good thinking (ways to transition from ordinary to critical thinking). He explains that an individual can interpret and defend their thinking with the use of particular skills. These sub-themes include, assuming, classifying and estimating (Lipman, 1987 , 2003 ). According to Lipman ( 2003 ), the use of these sub-themes supports an individual to transition from ordinary thinking to good thinking and allows one to provide sufficient reasons to support their opinions. To build on the sub-themes identified, Siswono ( 2010 ) suggests sense making (interpreting) requires examining, remembering and understanding the situation at hand. The theme and sub-themes identify dispositions of an ideal critical thinker to apply interpreting across a range of learning areas.

Analysing is found to be a further crucial component associated with critical thinking. Facione ( 2011 ) includes analysing as a core critical thinking skill in his definition, referring to analysing as both a cognitive skill and affective disposition. Lai ( 2011 ) defines analysing to include the analysis of arguments, judging, making inferences (inductive and deductive reasoning) and solving problems. Literature pertaining to analysing has identified a myriad of sub-themes that represent components of analysing in critical thinking (for example, Facione, 1990 ,  2011 ; Lai, 2011 ; Lipman, 1987 ; Siswono, 2010 ). The sub-themes identified have primarily emerged from a systematic review conducted by The American Philosophical Association (Facione, 1990 ) whereby dispositions that constitute critical thinking are identified in the following sub-themes: applying, conjecturing, drawing conclusions, hypothesising, inferring and noting relationships.

Evaluating is another inter-connected theme associated with critical thinking. This theme often occurs when someone evaluates their thought processes and evaluates their decision or the efficacy of their problem-solving technique (Alsaleh, 2020 ). Empirical evidence confirms critical thinking dispositions associated with evaluating support students to think critically (Facione & Facione, 2008 ). The most commonly cited dispositions (sub-themes) include assessing claims and making judgements (Facione, 1990 ), offering opinions and reasons (Lipman, 1987 ), making judgements with criteria (Lai, 2011 ; Lipman, 1987 ) and querying evidence (Facione, 1990 ). According to Bailin ( 2002 ), evaluating would be evident during domain-specific learning and can be transferable from one domain to another.

Ideal critical thinkers use explaining to broaden their thinking. However, it is important to note that explaining on its own might not constitute critical thinking. Fisher ( 2011 , p. 24) states that “working out an explanation” is more advanced than explaining something to another person. Similarly, Halpern ( 2013 ) states that providing reasons for the decisions made as well as the depth of detail explained would signify critical thinking. To further position explaining within critical thinking, sub-themes were identified, mainly by the seminal literature of Facione ( 1990 ). In particular, stating, presenting and justifying promote an individual’s skill to think critically. According to Facione ( 2011 ), using the sub-themes allows for someone to explain their thinking and the process they undertook to arrive at the judgement.

Innovative thinking or novel ideas are often exhibited when someone is creating (Facione, 2011 ). Creating or creative thinking is also aligned with critical thinking (Lipman, 1987 ). Siswono ( 2010 , p. 548) distinguishes creative thinking as “thinking that consists of non-algorithmic decision making”. Non-algorithmic decision-making is considered a complex approach to thinking where there are many possible solutions (Miri et al., 2007 ; Resnick, 1987 ). Lewis and Smith ( 1993 ) highlight higher-order thinking as a broader term that encapsulates “problem solving, critical thinking, creative thinking, and decision making” (p. 136). Sub-themes that an individual can apply to demonstrate creating are associated with evaluating and decision-making. One such sub-theme is self-regulating. Self-regulating is an action, similar to non-algorithm decision-making, whereby an individual self-evaluates their own inferences (Facione, 1990 ; Resnick, 1987 ). An individual that demonstrates self-regulating considers ways to revisit or review their learning prior to making final decisions. A self-regulator would consider conflicting conclusions or a review of their evidence (Facione, 2011 ). Sternberg ( 1986 ) identifies non-algorithmic decision-making as an element of critical thinking through his definition, “mental processes, strategies, and representations people use to solve problems, make decisions, and learn new concepts” (Sternberg, 1986 , p. 3).

Themes pertaining to young students’ mathematical thinking

There is a range ofliterature associated with mathematical thinking and mathematical understanding in the early years and primary years. What is prevalent in the literature is that in order for young students to engage in mathematical thinking, young students require multiple learning opportunities as well as a range of strategies. However, the strategies in the mathematical thinking literature show some commonality to the critical thinking literature reviewed above. For the purpose of this paper, we have aligned the mathematics literature to the critical thinking themes (cf. Monteleone, 2021 ). First, within the mathematical thinking literature, there was robust evidence of the two themes evaluating and explaining together with additional sub-themes associated with each of these themes. Second, while the two themes interpreting, and analysing, were not strong themes across the mathematical literature, there were additional identified sub-themes that contributed to these themes. Finally, there was no evidence of the theme creating within this review of the literature pertaining to mathematical thinking in the primary and early years. For these reasons, the next section focusses on further illuminating the themes and sub-themes associated with evaluating and explaining and additional identified sub-themes related to interpreting and analysing from the mathematics thinking literature.

Evaluating and explaining

The notion of young students evaluating their thinking is seen as central to thinking mathematically. For example, inviting students to evaluate a claim, thought processes or elaborate on an observation are identified by Cengiz et al. ( 2011 ) as key to extending students’ mathematical thinking. Additionally, a mathematical thinking framework created by Williams ( 2000 ) and extended by Wood et al. ( 2006 ) presents categorisations which increase in complexity that ultimately allow a student to evaluate their mathematical thinking. These researchers suggest that in order for students to effectively evaluate their mathematical thinking, they must first comprehend the problem, progress through applying, analysing and synthesising and finally engage in evaluating (Wood et al., 2006 ). This progression appears to align with the notion of evaluating, as evaluating is identified as a problem-solving technique or solution process in the critical thinking literature (Alsaleh, 2020 ). Similarly, Cengiz et al. ( 2011 ) study considers the type of learning that can support students to evaluate their mathematical thinking. It appears that during classroom discussions, the theme of evaluating dominated students’ responses (Cengiz et al., 2011 ; Franke & Kazemi, 2001 ; Wood et al., 2006 ). Additionally, the mathematical thinking literature agreed that making judgements with criteria (Cengiz et al., 2011 ), solving ; (Francisco & Maher, 2005 ) and offering their opinions with reasons (Cengiz et al., 2011 ) were sub-themes of evaluating. Findings from these studies also indicate that the skill of evaluating occurs when the tasks included mathematical problems that allow students to identify mathematical language and make connections with other mathematical concepts. Thus, it is evidenced that the types of tasks set and classroom discussions that occurred contribute to students’ ability to evaluate their thought process and their problem-solving techniques.

Explaining is considered a key mathematical thinking theme often aligned with literature pertaining to reasoning or justifying, focusing on students explaining the “how” and “why” (reasoning, justifying) rather than the “what” (stating, presenting), which aligned to the critical thinking literature. At times within the literature, the terms reasoning and justifying were seen as interchangeable, and other times, they were separated with distinct features. In addition, the definition of the terms seemed to closely align with each study’s aims and methodology (e.g., Diezmann et al., 2001 ; Melhuish et al.,  2020 ; Wood et al., 2006 ). However, across the definitions, there are common features. These include defending solutions, providing evidence, making conjectures and presenting logical argument. Studies that focused on students’ reasoning or justifying have also identified that the way the learning experience is framed can provide a platform for young students to reason and justify (Anthony et al., 2015 ; Hunter & Anthony, 2011 ; Papandreou & Tsiouli, 2020 ; Papic et al., 2009 ; Vale et al., 2017 ).

Findings from these studies ascertained that a focus on mathematical practices over time that promote and scaffold student participation, in particular opportunities for talk, resulted in students explaining their own mathematical ideas and other students’ ideas and solutions more regularly in class (Cengiz et al., 2011 ; Hufferd-Ackles et al., 2004 ; Hunter & Anthony, 2011 ). These findings further support the notion that the types of tasks set and the classroom discussions that occur are crucial to allowing students to explain and evaluate their own and other students’ mathematical thinking.

Interpreting and analysing

The mathematical thinking literature review also agreed that the sub-themes that support students to interpret the mathematics include estimating (Clarke & Kamii, 1996 ; Clements & Sarama, 2020 ; Lambdin & Walcott, 2007 ; Sowder, 1992 ), remembering (Cengiz et al., 2011 ; Fraivillig et al., 1999 ) and understanding (Bobis et al., 2005 ; Cengiz et al., 2011 ; Fraivillig et al., 1999 ; Jacobs et al., 2010 ; Mulligan et al., 2020 ). From a mathematical thinking perspective, estimating has progressed from a simple “guess” to a sophisticated process required to interpret mathematics (Clements & Sarama, 2020 ). Estimating is evidenced across a range of mathematical concepts: (1) measurement (e.g., estimating the length of a room), (2) numerosity (e.g., estimating the number of people on a bus) and (3) mathematical operations (e.g., estimating how much 12 × 20 is) (Sowder, 1992 ). Remembering has been found to build on students already established mathematical thinking and to then extend their thinking to include new information (Fraivillig et al., 1999 ). Similarly, understanding has been identified as a strategy to assist students’ and further challenge students to interpret their mathematical thinking (Fraivillig et al., 1999 ) and transfer their understandings to other mathematical concepts (Mulligan et al., 2015 ). Therefore, based on the mathematical thinking literature, a student can interpret (make sense of the mathematics) by using the sub-themes of estimating , remembering and understanding .

Adding on to the already identified sub-themes associated with analysing, the review of the mathematical thinking literature evidenced that the sub-themes noting relationships (Papandreou & Tsiouli, 2020 ) and grasping principles (Fennema et al., 1998 ) support young students’ mathematical thinking. While noting relationships was also evidenced in the critical thinking literature, a mathematical thinking perspective by Papandreou and Tsiouli ( 2020 ) highlighted how children’s use of representations (blocks, illustrations, written work, body movement or gestures) during mathematics free time provided opportunities for young students to note relationships and grasp principles . Thus, to grasp principles is an additional sub-theme that emerged from this review. Fennema et al. ( 1998 ) found that when students used a variety of ways to display their mathematical understandings, they were able to grasp principles and apply these principles to tackle more complex mathematical problems as they progressed through the grades. Although these two sub-themes, noting relationships and grasping principles , are identified as separate terms in the mathematical thinking literature, they both assist students to analyse their mathematical thinking.

The themes and sub-themes cited in accordance with the critical thinking and mathematical thinking literature provided five themes with several associated sub-themes. Table 1 presents themes pertaining to critical thinking and mathematical thinking. The review of literature identified thirty sub-themes across the critical thinking and mathematical thinking literature. At times, mathematical thinking sub-themes were categorised with critical thinking themes, for example, the sub-theme of grasping principles (mathematical thinking) is under the theme of analysing (critical thinking). This is due to the way the sub-theme was described in the literature. Many sub-themes are associated with critical thinking (presented in column 2); however, some sub-themes were present in both sets of literature (presented in column 3) with only two emerging solely from the mathematical thinking literature review (presented in column 4).

The review and synthesise of the literature pertaining to both mathematical thinking and critical thinking have led to the amalgamation of the terms as critical mathematical thinking (CMT) and the development of a literature informed conceptual framework to situate the construct CMT. There is little research to suggest that the term CMT exists as a notion, nor was it evident that there had previously been a conceptualization of CMT as a framework. Thus, the review of literature provided an opportunity to blend critical thinking and mathematical thinking to provide a literature informed conceptual framework for defining the term CMT which is then applied to understand the CMT capabilities presented by young students as they enter formal schooling.

Research design

The data reported in this paper are derived from a larger mixed method study. The larger study (Monteleone, 2021 ), which included 161 students, aimed to investigate CMT in young students and the teaching actions/questions that help young students to exhibit their CMT. The data in this paper reports on the qualitative student data of the larger study. The research question addressed in this paper includes what are the CMT capabilities young students exhibit as they begin formal schooling? As the participants were young students, and the purpose was to identify their CMT capabilities, the data collection process included a task-based clinical interview. The conceptual framework presented in Table 1 forms the basis of the qualitative component of the study and is used as a lens to analyse the student data.

Participants

In total, 161 kindergarten students, aged between 5 years and 1 month to 6 years and 8 months of age, participated in the larger study (Monteleone, 2021 ). These students were from three primary schools located in New South Wales Australia all within an urban setting in southern Sydney. The schools had similar demographics and ranges in the Index of Community Socio-Educational Advantage (ICSEA) level (1092–1112). The ICSEA score above 1000 indicates schools that are considered socio-economically advantaged. Finally, the average Numeracy National Assessment Program—Literacy and Numeracy (NAPLAN) results were similar and above the Australian average results. Informed written consent was obtained from principals, teachers, parents and students before data collection commenced.

High CMT students

As the larger study moved through different stages of data collection, including quantitative measures, the participants were narrowed from 161 students to include 16 students that displayed high levels of CMT in alignment with the literature informed conceptual framework. These 16 students are the focus of this paper and were identified as high CMT students. The students were selected across the three schools with four students from School A (25% of the sample from School A), five students from School B (32% of the sample from School B) and seven students from School C (43% of the sample from School C) (16 students in total). In summary of the 16 high CMT students, nine were male, and seven were female.

Data collection

The larger mixed method study included quantitative measures that assisted in the purposeful selection of participants. For the purpose of this paper, findings from the one-on-one task-based interview are drawn on to evidence and illustrate the types of critical mathematical thinking of young learners. All 16 high CMT students participated in the video recorded interviews conducted by the researcher. On average, each interview was 20 min.

Task-based one-on-one interviews

A task-based one-on-one clinical interview schedule, the Critical Mathematical Thinking Learning Experiences (CMTLE) consisting of eight learning experiences, was used with the high CMT students (n = 16). The process of a clinical interview has roots in Piaget’s methode clinique (Hunting & Doig,  1997 ) that identifies children’s cognitive ability within the social context of the learning. Piaget included specific methods and strategies tailored to children so that he could observe their behaviour. In mathematics education, clinical research methods are common approaches to assessing young children’s mathematical learning (Hunting & Doig,  1997 ; Ginsburg, 2005 ; Opper, 1977 ; Sarama & Clements, 2009 ; Warren et al., 2012 ).

A clinical interview involves many methods and strategies. They include intensively working one-on-one with an individual child, an ongoing conversation between the adult and the child and the inclusion of flexible questioning based on how the child is interacting (Ginsburg, 2005 ; Posner & Gertzog, 1982 ). Clinical interview methods highlight language as a significant component. The dialogue between the participant and the researcher supported the researcher to clarify, ask questions and pose problems during the CMTLE interview. According to Hunting and Doig ( 1997 ), the questioning should be open-ended in design, include freedom of choice in responses, maximise discussion opportunities and allow for the researcher and the student to reflect on the process.

Design of the CMTLE

For the purpose of this study, each learning experience of the CMTLE was designed to include (i) a pre-planned mathematics learning experience with an open-ended question (Nicol & Bragg, 2009 ; Sullivan & Lilburn, 1997 ) posed to students, (ii) opportunities for multiple entry points (Jorgensen et al., 2010 ) and (iii) appropriate physical manipulatives (concrete material or a visual stimulus) (Cooper & Warren,  2007 ; Lingefjärd, & Ghosh, 2016 ; MacDonald & Lowrie, 2011 ) to support the experience. Designing each learning experience to be an open-ended experience provided the opportunity for students to solve the problem in multiple ways.

In addition, each learning experience covered a range of mathematical content that drew from all strands of the Australian mathematics curriculum appropriate for this age group. For example, learning experience one allowed for the young student to apply their mathematical understanding in the following ways: estimating, two-dimensional space, estimation of half, coordinating the middle point using two dimensions and symmetry. Before implementing the task-based interviews, the following was conducted: (i) each learning experience was trialled with a group of young students; (ii) member checking was conducted with other experts in mathematics education; and (iii) the classroom teachers were consulted to ensure these learning experiences (and relevant mathematical content) had not previously occurred in mathematics lessons. Table 2 presents learning experience one including the physical manipulatives and examples of the teacher questions used when implementing the learning experiences.

The additional seven learning experiences included young students identifying strategies to count unseen objects; making connections with addition understandings; identifying taller towers with the use of different manipulatives; using manipulatives for a real world subtraction problem; identifying the amount of floor tiles required; equally halving irregular shapes and using spatial awareness to replicate an irregular shape.

The administration of the CMTLE took between 25 and 35 min for each student. The learning experiences were administered using a one-on-one clinical interview. All CMTLE interviews were video recorded to capture both the student responses and researchers questioning. One video camera was set up on a tripod focusing on the student and researcher. These videos were downloaded at the conclusion of the student interviews and were later transcribed for data analysis. In addition to this, the researcher also took notes and collected student work samples produced during the CMTLE.

Data analysis of the CMTLE interview

At the conclusion of the administration of the CMTLE, the high CMT students ( n  = 16) videos were transcribed. To analyse CMT capabilities, one researcher identified components within each high CMT student transcript that aligned with the CMT conceptual framework (see Table 1 ). The other researchers were consulted during the analysis phase and development of the coding systems. The CMT conceptual framework themes and sub-themes were coded for across the entire transcript, including both the student’s and researcher’s utterances. At the conclusion of the coding, all authors met to discuss the codes and examples provided. Once there was agreement, frequencies were calculated for each theme and sub-theme and provided a summary of the student responses. If a work sample was available or produced by the student, the researcher included the work sample in the table and was a part of the analysis process. Figure  1 provides an example of the collation and coding of the transcription from one student’s response for learning experience one. This is an example of the explaining theme aligned to the CMT conceptual framework.

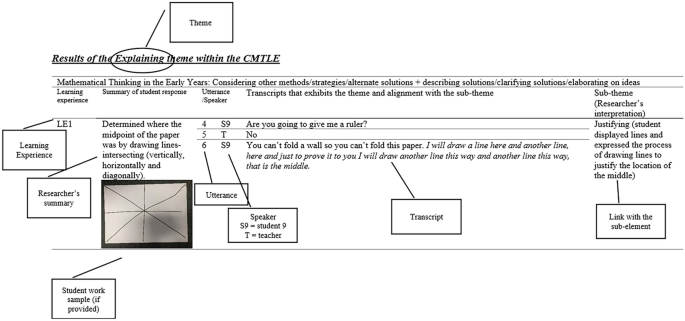
Example of coding of transcripts using the themes and sub-themes of the CMT conceptual framework

As depicted in Fig.  1 , the first column identifies the learning experience. Column two is a summary of the student response and the inclusion of a work sample. The third column (utterance/speaker) records when the particular response occurred in the interview. For example, 4 indicates it is the fourth utterance in the interview, and T indicates that the teacher said this utterance. S9 references student 9 in the study, and T references the teacher. The transcript section that aligns with CMT is added to the next column. The final column is the researcher’s interpretation in alignment with the CMT conceptual framework sub-themes. The purpose of this process was to identify the capabilities of high CMT students.

The full analysis of the high CMT student data were coded under the following CMT conceptual framework themes and sub-themes (see Table 1 ).

Findings to support CMT in young students

Across the full analysis of the data pertaining to the alignment of the 16 high CMT students , there were 53 instances that evidenced critical mathematical thinking. The analysis of data identified that occurrences appeared more than once in a student’s transcript. Table 3 presents the CMT theme, the sub-theme, examples from the transcripts related to learning experience one and the frequency across all eight learning experiences.

Students exhibited responses pertaining to all five themes of the CMT conceptual framework. The most frequent theme identified in the analysis of the transcripts was explaining (20), followed by evaluating (12). The least frequent theme identified in the analysis of the transcripts was creating (6).

The descriptions that emerged from the data analysis provided a nuanced understanding of some of the sub-themes when young students are engaged in critical mathematic thinking. It was evident that there are defined CMT capabilities in young students and these align with aspects of the CMT conceptual framework that emerged from the literature. However, the in-depth data analysis found that while all five themes were present in the qualitative data, not all sub-themes were evidenced in the young students in the study. Therefore, five themes and 14 sub-themes emerged from the data analysis.

Critical mathematical thinking framework for young students

Results from this study refined the identified themes and sub-themes in the literature and provided a succinct version of a framework that begins to structure the CMT found in young students (between 5 years and 1 month to 6 years and 8 months of age) who participated in this study. The findings are related to what the 16 high CMT students displayed; however, a larger sample may allow for the expansion of the CMT conceptual framework. There were two key findings in relation to the refinement of the CMT conceptual framework.

First, the initial identified five themes were evident in the student responses; however, some were more evident than others. It appeared for these young students that explaining was the most prominent critical mathematical thinking skill displayed in their responses. The factors that may have contributed to explaining being the most prominent may include the age of the participants, the design of the tasks and the types of teacher questions posed. This was followed by evaluating. There was limited evidence of creating , interpreting , and analysing in the data.

Second, the findings from the study identified fewer sub-themes than originally presented in the CMT conceptual framework (see Fig.  2 ). For example, the theme in which most sub-themes were not evidenced was the theme interpreting and thus will be used as an illustrative example . The identified sub-themes drew on several researchers’ work in relation to mathematical and critical thinking (for example, Facione, 1990 ; Facione & Facione, 2008 ; Lipman, 1987 ; Siswono, 2010 ). For this particular theme, the two sub-themes that were most identified in the high CMT students ( n  = 16) were clarifying and estimating.

CMT Conceptual Framework for Young Students (CMTFYS)

As only two of the eleven sub-themes were evidenced in the theme interpreting , it could, therefore, be hypothesised that this occurred for one or more of the following two reasons: (a) The other sub-themes were difficult to identify in student responses from the suite of eight CMTLE presented to these young students; (b) there is overlap between the sub-themes identified in the critical thinking literature (for example, aspects of categorising and examining form dimensions of noting relationships). Thus, in general, the definition of the sub-themes and the overlap between and across sub-themes identified in the literature requires further investigation.

Figure  2 presents the final version of the conceptual framework, now titled, Critical Mathematical Thinking Framework for Young Students (CMTFYS) with the themes and sub-themes. In addition, sub-themes within each theme are ordered from the most frequent to the least frequent.

Both sets of literature the critical thinking literature and the mathematical thinking literature are represented in the CMTFYS. The five themes that emerged from the results of this study aligned with the five themes that were identified in the literature review. The themes, interpreting, analysing and creating emerged from the critical thinking literature while evaluating and explaining emerged from both critical thinking and mathematical thinking literature.

Limitations and future directions

There are a number of potential limitations to consider from the interpretation of findings which can provide direction for future research. One limitation was that the findings in this paper focused on a small sample of young students, resulting in limited generalisations drawn from the data. However, the data provided rich descriptive information about young students’ CMT and teacher methods to exhibit CMT. As a second limitation, the young students were from similar schools in NSW. We suggest the study is repeated with more young students in various school and early learning settings to provide transferability of results. Third, the learning experiences were intended for implementation prior to the young students engaging in similar content or learning in class. It would be beneficial to ensure a repeat of the study was to occur in advance of too much school-based teaching input.

It is imperative that further research in CMT can take these factors into consideration. The findings of the study highlight the importance of the CMTFYS as a platform for teachers to support young students to exhibit CMT. It is by fully understanding CMT and the themes and sub-themes of the CMTFYS that teaching and learning practices will be modified to support young students in their mathematics learning. As the data reported in this paper is a part of a larger mixed method study, future papers will report on other key finding which includes a proposed model to support teacher questioning to exhibit young students’ CMT and how the model can influence approaches teachers use.

In order to address the aim of the paper, the findings are aligned to the research question, what are the CMT capabilities young students exhibit as they begin formal schooling? First, the use of the Critical Mathematical Thinking Framework for Young Students is a unique contribution to the research literature and supports the definition and conceptualisation of critical mathematical thinking for young students. Additionally, the blending of both sets of literature (critical thinking and mathematical thinking) and the refinement of themes and sub-themes supported the formation of the notion of CMT, a domain specific thinking with critical thinking. A second finding of this study suggest that a literature and data informed conceptual framework—CMTFYS is required to support teachers in identifying CMT in young students. The analysis of data and identification of findings highlight that the development and use of a conceptual framework (CMTFYS) supports the definition of CMT capabilities in young students. The definition in the CMTFYS is presented as five themes and 14 sub-themes . As discussed, there are differing views as to whether critical thinking is subject specific or standalone. A body of literature supports domain-specific knowledge as a requirement for critical thinking (Bailin, 2002 ), whereas Facione ( 1990 ) and Facione and Facione ( 2008 ) believe critical thinking is across all content or subject areas. The CMTFYS supports and extends on the literature that critical thinking is subject specific.

Conclusions drawn from this study confirm that CMT can be evidenced in young students. New insights are gained into CMT presented by young students in two ways. First, findings presented from this study offer a unique contribution with the development of the CMTFYS. Furthermore, the CMTFYS is specific to young students and can be considered for use in both prior to school early learning settings and formal primary school classes. Second, the data from the young students used for the refinement of the CMTFYS demonstrated sophisticated CMT. More instances of identifying such thinking from young students can shift the ways teachers plan for mathematics learning.

Based on the conclusions of this study, there are implications for curriculum, teaching and learning, and recommendations for teaching and research with the future application of CMTFYS.

A practical implication from this study is that the curriculum (both national and international e.g., Australia; Singapore; NCTM) for students in their first year of formal schooling includes the themes and sub-themes of the CMTFYS. Within an international context, the CMTFYS has potential to provide a nuanced framework to support and scaffold how young students exhibit critical mathematical thinking and how this differs to, and or aligns with, the identified mathematical processes in the curriculum (e.g., how does CMT for young students align with problem solving, reasoning and proof, communication, connections and representations as identified by NCTM). In the Australian context, this could be in the form of mathematics proficiencies (problem solving, understanding, reasoning, fluency) that are also supported through the critical thinking general capability (ACARA, 2014 ). It is anticipated that the CMTFYS has the potential to provide clarification of what specific mathematics proficiencies are for young students and will assist teachers in identifying CMT during mathematics learning experiences. This will provide a better understanding of how critical thinking is exhibited within the specific subject domain of mathematics.

The results from this study can enhance teachers’ knowledge about CMT. Therefore, it is recommended further understanding of CMT is required by teachers of young students. In addition, teachers can consider ways in which open-ended learning experiences can be embedded in their practice.

This study has framed a new term in mathematics educational research, critical mathematical thinking, and has evidenced how this conceptual framework can be applied to a research study with young learners. It is apparent that there is more work to be undertaken in this space with a larger sample of students from a range of contexts to continue to develop and refine or expand the conceptual framework and application of the framework across the primary school setting. Despite this, the application of the conceptual framework as a means to better understand the critical mathematical thinking capabilities for young students presents a contemporary shift in the literature that continues to support the strengths young children bring to the mathematics classroom as they begin school.

Data Availability

The datasets generated during and/or analysed during this study are not publicly available due to ethical considerations but are available from the corresponding author on reasonable request.

Ab Kadir, M. A. (2018). An inquiry into critical thinking in the Australian curriculum: Examining its conceptual understandings and their implications on developing critical thinking as a “general capability” on teachers’ practice and knowledge. Asia Pacific Journal of Education, 38 (4), 533–549. https://doi.org/10.1080/02188791.2018.1535424

Article   Google Scholar  

Alsaleh, N. J. (2020). Teaching critical thinking skills: Literature review.  Turkish Online Journal of Educational Technology-TOJET, 19(1), 21–39.

Animasaun, I. L. (2021). Significance of offering further mathematics and personal interest in mathematics on some variables common to secondary school students. International Journal of Learning and Change, 13 (6), 640–655.

Anthony, G., Hunter, J., & Hunter, R. (2015). Supporting prospective teachers to notice students’ mathematical thinking through rehearsal activities. Mathematics Teacher Education and Development, 17 (2), 7–24.

Google Scholar  

Australian Curriculum, Assessment and Reporting Authority. (2014). General capabilities. https://www.australiancurriculum.edu.au/f-10-curriculum/general-capabilities#

Bailin, S. (2002). Critical thinking and science education. Science & Education, 11 (4), 361–375.

Bobis, J., Clarke, B., Clarke, D., Thomas, G., Wright, B., Young-Loveridge, J., & Gould, P. (2005). Supporting teachers in the development of young children’s mathematical thinking: Three large scale cases. Mathematics Education Research Journal, 16 (3), 27–57. https://doi.org/10.1007/bf03217400

Burrus, J., Jackson, T., Xi, N., & Steinberg, J. (2013). Identifying the most important 21st century workforce competencies: An analysis of the Occupational Information Network (O* NET). ETS Research Report Series, 2013 (2), i–55. https://doi.org/10.1002/j.2333-8504.2013.tb02328.x‌

Cengiz, N., Kline, K., & Grant, T. J. (2011). Extending students’ mathematical thinking during whole-group discussions. Journal of Mathematics Teacher Education, 14 (5), 355–374. https://doi.org/10.1007/s10857-011-9179-7

Clark, F. B., & Kamii, C. (1996). Identification of multiplicative thinking in students in grades 1–5. Journal for Research in Mathematics Education , 27, 41–51.

Clarke, B., Cheeseman, J., & Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Mathematics Education Research Journal, 18 (1), 78–102. https://doi.org/10.1007/bf03217430

Clements, D. H., & Sarama, J. (2011). Early childhood teacher education: The case of geometry. Journal of Mathematics Teacher Education, 14 (2), 133–148.  https://doi.org/10.1007/s10857-011-9173-0

Clements, D. H., & Sarama, J. (2020).  Learning and teaching early math: The learning trajectories approach . Routledge.

Cooper, T. J., & Warren, E. (2007). The effect of different representations on Years 3 to 5 students’ ability to generalise. ZDM, 40(1), 23–37. https://doi.org/10.1007/s11858-007-0066-8

Davies, W. M. (2006). An ‘infusion ‘approach to critical thinking: Moore on the critical thinking debate. Higher Education Research & Development, 25 (2), 179–193. https://doi.org/10.1080/07294360600610420

Department of Education, Employment and Workplace Relations. (2022). Belonging, being and becoming: the Early Years Learning Framework for Australia . V2.0. Barton: Commonwealth of Australia.

Diezmann, C.M., Watters, J. J., & English, L. D. (2001) Implementing mathematical investigations with young children. In Proceedings 24th Annual Conference of the Mathematics Education Research Group of Australasia , pages 170–177, Sydney.

Doig, B., & Ompok, C. (2010). Assessing young children’s mathematical abilities through games. Procedia - Social and Behavioral Sciences, 8 , 228–235. https://doi.org/10.1016/j.sbspro.2010.12.031

Elder, L., & Paul, R. (2020). Fact over fake: A critical thinker’s guide to media bias and political propaganda. Foundation for Critical Thinking.

Ellerton, P. (2018). On critical thinking and collaborative inquiry.  Forthcoming, and to be presented at the SFU critical thinking round table in February .

Ennis, R. H. (1992). The degree to which critical thinking is subject specific: Clarification and needed research. The generalizability of critical thinking: Multiple perspectives on an educational ideal , 21–37.

Ennis, R. H. (2013). Critical thinking across the curriculum: The wisdom CTAC program. Inquiry: Critical Thinking Across the Disciplines, 28 (2), 25–45.

Facione, P. A. (1990). Critical thinking: A statement of expert consensus for purposes of educational assessment and instruction . The California Academic Press.

Facione, P. A. (2011). Critical thinking: What it is and why it counts.  Insight assessment, 2007(1), 1–23.

Facione, N. C., & Facione, P. A. (2008). Critical thinking and clinical judgment.  Critical thinking and clinical reasoning in the health sciences: A teaching anthology , 1–13.

Fennema, E., Carpenter, T. P., Jacobs, V. R., Franke, M. L., & Levi, L. W. (1998). A longitudinal study of gender differences in young children’s mathematical thinking. Educational Researcher, 27 (5), 6–11.

Ferrini-Mundy, J. (2000). Principles and standards for school mathematics: A guide for mathematicians.  Notices of the American Mathematical Society ,  47 (8).

Fisher, A. (2011).  Critical thinking: An introduction . Cambridge University Press.

Fraivillig, J. L., Murphy, L. A., & Fuson, K. C. (1999). Advancing children’s mathematical thinking in everyday mathematics classrooms. Journal for Research in Mathematics Education, 30 (2), 148–170.

Francisco, J. M., & Maher, C. A. (2005). Conditions for promoting reasoning in problem solving: Insights from a longitudinal study. The Journal of Mathematical Behavior, 24 (3–4), 361–372.

Franke, M. L., & Kazemi, E. (2001). Learning to teach mathematics: Focus on student thinking. Theory into Practice, 40 (2), 102–109. https://doi.org/10.1207/s15430421tip4002_4

Ginsburg, H. (2005).  Entering the child’s mind: The clinical interview in psychological research and practice . Cambridge University Press.

Groves, S. (2012). Developing mathematical proficiency. Journal of Science and Mathematics Education in Southeast Asia, 35 (2), 119–145.

Halpern, D. F. (2013).  Thought and knowledge: An introduction to critical thinking.  Psychology Press.

Heard, J., Scoular, C., Duckworth, D., Ramalingam, D., & Teo, I. (2020). Critical thinking: Skill development framework. The Australian Council for Educational Research Ltd.

Hufferd-Ackles, K., Fuson, K. C., & Sherin, M. G. (2004). Describing levels and components of a math-talk learning community. Journal for Research in Mathematics Education, 35 (2), 81–116. https://doi.org/10.2307/30034933

Hunter, R., & Anthony, G. (2011). Forging mathematical relationships in inquiry-based classrooms with Pasifika students. Journal of Urban Mathematics Education, 4 (1), 98–119.

Hunting, R. P., & Doig, B. A. (1997). Clinical assessment in mathematics: Learning the craft. Focus on Learning Problems in Mathematics, 19 (3), 29–48.

Hunting, R., & Pearn, C. (2009). Mathematical thinking of young children through the eyes of preschool practitioners. In Crossing divides: Proceedings of the 32nd annual conference of the Mathematics Education Research Group of Australasia (vol. 1).

Jacobs, V. R., Lamb, L. L. C., & Philipp, R. A. (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education, 41 (2), 169–202. https://doi.org/10.5951/jresematheduc.41.2.0169

Jorgensen, R., Grootenboer, P., Niesche, R., & Lerman, S. (2010). Challenges for teacher education: The mismatch between beliefs and practice in remote Indigenous contexts. Asia Pacific Journal of Teacher Education, 32 (2), 161–175.Kim, Y. H. (2011). Prospective early childhood educators’ meta-cognitive knowledge and teacher self-efficacy: exploring domain-specific associations. Educational Psychology, 31 (6), 707–721. https://doi.org/10.1080/01443410.2011.599924

Lai, E. R. (2011). Critical thinking: A literature review. Pearson’s Research Reports, 6 , 40–41.

Lambdin, D. V., & Walcott, C. (2007) Connections between psychological learning theories and the elementary school curriculum. In G. Martin & M. Strutchens (Eds.), The sixty-ninth annual yearbook of the National Council of Teachers of Mathematics. Reston: National Council of Teachers of Mathematics.

Lewis, A., & Smith, D. (1993). Defining higher order thinking. Theory into Practice, 32 (3), 131–137.

Lingefjärd, T., & Ghosh, J. B. (2016). Learning mathematics as an interplay between internal and external representations.  Far East Journal of Mathematical Education ,  16 (3), 271–297. https://doi.org/10.17654/me016030271

Lipman, M. (1987). Critical thinking—What can it be? Educational Leadership, 46 (1), 38–43.

Lipman, M. (2003). Thinking in education . Cambridge University Press.

Book   Google Scholar  

MacDonald, A., & Lowrie, T. (2011). Developing measurement concepts within context: Children’s representations of length. Mathematics Education Research Journal, 23 (1), 27–42. https://doi.org/10.1007/s13394-011-0002-7

MacDonald, A., & Carmichael, C. (2018). Early mathematical competencies and later achievement: Insights from the Longitudinal Study of Australian Children. Mathematics Education Research Journal, 30 (4), 429–444. https://doi.org/10.1007/s13394-017-0230-6

McGaw, B., Louden, W., & Wyatt-Smith, C. (2020). NAPLAN Review Final Report.

Melhuish, K., Thanheiser, E., & Guyot, L. (2020). Elementary school teachers’ noticing of essential mathematical reasoning forms: Justification and generalization. Journal of Mathematics Teacher Education, 23 (1), 35–67. https://doi.org/10.1007/s10857-018-9408-4

Miri, B., David, B. C., & Uri, Z. (2007). Purposely teaching for the promotion of higher-order thinking skills: A case of critical thinking. Research in Science Education, 37 (4), 353–369. https://doi.org/10.1007/s11165-006-9029-2

Monteleone, C. (2021). Critical mathematical thinking in young students [Doctoral this, Australian Catholic University]. Australia. https://acuresearchbank.acu.edu.au/item/8x1z9/critical-mathematical-thinking-in-young-students

Moore, T. (2013). Critical thinking: Seven definitions in search of a concept. Studies in Higher Education, 38 (4), 506–522. https://doi.org/10.1080/03075079.2011.586995

Mulligan, J., Mitchelmore, M., & Stephanou, A. (2015). Patterns and structure assessment: An assessment program for early mathematics (F - 2) Teacher Guide . Australia: Australian Council for Educational Research.

Mulligan, J., Oslington, G., & English, L. (2020). Supporting early mathematical development through a “pattern and structure” intervention program. ZDM Mathematics Education . https://doi.org/10.1007/s11858-020-01147-9

National Council of Teachers of Mathematics. (2000a). Principles and standards for school mathematics . Reston, VA, USA: The National Council of Teachers of Mathematics.

National Council of Teachers of Mathematics. (2000b). Principles and standards for school mathematics. In Grades K - 4: Standard 3: Mathematics as Reasoning, Reston, VA: The National Council of Teachers of Mathematics.

Nicol, C., & Bragg, L. (2009). Designing problems: What kinds of open-ended problems do preservice teachers pose? Proceedings of 33rd Annual Meeting of the International Group for the Psychology of Mathematics Education (pp. 225–232). PME.

Opper, S. (1977). Piaget’s clinical method. Journal of Children’s Mathematical Behaviour, 1 (4), 90–107.

Papandreou, M., & Tsiouli, M. (2020). Noticing and understanding children’s everyday mathematics during play in early childhood classrooms.  International Journal of Early Years Education , 1–18. https://doi.org/10.1080/09669760.2020.1742673

Papic, M., & Mulligan, J. (2005). Pre-schoolers’ mathematical patterning. In P. Clarkson, A. Downton, D. Gronn, M. Horne, A. McDonough, R. Pierce, & A. Roche (Eds.),  Proceedings of the 28th annual conference of the Mathematics Education Research Group of Australasia  (Vol. 2, pp. 609–616). Sydney, Australia: Program Committee.

Papic, M., Mulligan, J., & Bobis, J. (2009). Developing mathematical concepts in Australia pre-school settings: Children’s mathematical thinking . Paper presented at the MERGA, New Zealand.

Perry, B., MacDonald, A., & Gervasoni, A. (2015). Mathematics and transition to school: Theoretical frameworks and practical implications. In  Mathematics and Transition to School  (pp. 1–12). Springer, Singapore.

Posner, G. J., & Gertzog, W. A. (1982). The clinical interview and the measurement of conceptual change.  Science Education ,  66 (2), 195–209.

Rios, J. A., Ling, G., Pugh, R., Becker, D., & Bacall, A. (2020). Identifying critical 21st-century skills for workplace success: A content analysis of job advertisements. Educational Researcher, 49 (2), 80–89. https://doi.org/10.3102/0013189x19890600

Resnick, L. B. (1987). Education and learning to think . National Academy Press.

Sarama, J., & Clements, D. H. (2009). Early childhood mathematics education research:  Learning trajectories for young children . New York Routledge.

Scammacca, N., Fall, A.-M., Capin, P., Roberts, G., & Swanson, E. (2020). Examining factors affecting reading and math growth and achievement gaps in grades 1–5: A cohort-sequential longitudinal approach. Journal of Educational Psychology, 112 (4), 718–734. https://doi.org/10.1037/edu0000400

Skovsmose, O. (1994). Towards a critical mathematics education. Educational Studies in Mathematics, 27 (1), 35–57. https://doi.org/10.1007/bf01284527

Siswono, T. (2010). Leveling students’ creative thinking in solving and posing mathematical problem. Indonesian Mathematical Society Journal on Mathematics Education, 1 (1), 17–40.

Sowder, J. T. (1992). Making sense of numbers in school mathematics. In G. Leinhardt, Putman, & R. A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching (pp. 1–45). Mahwah, NJ: Lawrence Erlbaum Associates.

Sternberg, R. J. (1986). Critical thinking: Its nature, measurement, and improvement National Institute of Education.

Sullivan, P., & Lilburn, P. (1997). Open-ended maths activities: Using “good” questions to enhance learning: Oxford University Press.

Thomson, S., Wernert, N., Rodrigues, S., & O'Grady, E. (2020). TIMSS 2019 Australia highlights.

Uribe-Enciso, O. L., Enciso, D. S. U., Daza, M., & d. P. V. (2017). Critical thinking and its importance in education: Some reflections. Rastros Rostros, 19 (34), 78–88.

Vale, C., Widjaja, W., Herbert, S., Bragg, L. A., & Loong, E.Y.-K. (2017). Mapping variation in children’s mathematical reasoning: The case of ‘what else belongs?’ International Journal of Science and Mathematics Education, 15 (5), 873–894.

Watson, G., & Glaser, E. (2002). Watson-Glaser critical thinking appraisal (UK). Psychological Corporation.

Williams, G. (2000). Collaborative problem solving and discovered complexity. Mathematics Education beyond, 2 , 656–663.

Wood, T., Williams, G., & McNeal, B. (2006). Children’s mathematical thinking in different classroom cultures. Journal for Research in Mathematics Education, 37 (3), 222–255.

Download references

Open Access funding enabled and organized by CAUL and its Member Institutions.

Author information

Authors and affiliations.

Australian Catholic University, NSW, Australia

Chrissy Monteleone

The University of Queensland, Brisbane, Australia

Jodie Miller & Elizabeth Warren

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Chrissy Monteleone .

Ethics declarations

Ethical approval and informed consent.

In adhering to ethical guidelines set out by the Australian Catholic University (ACU) and in conjunction with the Australian National Statement on Ethical Conduct in Human Research, ethical clearance to conduct this research was approved (2014212N). We obtained informed consent from the principals, teachers, parents and children in the class.

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Missing Open Access funding information has been added in the Funding Note.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Monteleone, C., Miller, J. & Warren, E. Conceptualising critical mathematical thinking in young students. Math Ed Res J 35 , 339–359 (2023). https://doi.org/10.1007/s13394-023-00445-1

Download citation

Received : 30 November 2021

Revised : 01 September 2022

Accepted : 23 January 2023

Published : 08 February 2023

Issue Date : June 2023

DOI : https://doi.org/10.1007/s13394-023-00445-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Critical thinking
• Mathematical thinking
• Critical mathematical thinking
• Early years
• Find a journal
• Publish with us
• Track your research