unit 1 equations and inequalities homework 6 absolute value inequalities

Solving Absolute Value Equations and Inequalities

As we saw earlier in the Negative Numbers and Absolute Value section, an absolute value  (designated by |  |) means take the positive value of whatever is between the two bars. The absolute value is always positive, so you can think of it as the distance from 0 . As an example, $ \left| 3 \right|=3$ and $ \left| {-3} \right|=3$. It’s as simple as that!

(Note that we also address absolute values here in the Piecewise Functions section  and  here in the Rational Functions, Equations, and Inequalities section .)

Solving Absolute Value Equations

Solving absolute equations  isn’t too difficult; just have to separate the equation into two different equations (once we isolate the absolute value), since we don’t if what’s inside the absolute value is  positive  or  negative . Then, make the expression on the right-hand side (without the variables) both positive and negative and solve each equation; typically, we will get two answers . We must  check our answer s , since we may get  extraneous solutions (solutions that don’t work). .

There are a few cases with absolute value equations or inequalities where we don’t have to even solve! One is when we have isolated the absolute value, and it is set equal to a negative number , such as $ \left| {x-5} \right|=-4$, or $ \left| {x-5} \right|\le -4$, for example. Since an absolute value can never be negative , we have  no solution for this case. The other is when the absolute value is greater than a negative number, such as  $ \left| {x-5} \right|>-4$  for example. In this case our answer is all real numbers , since an absolute value is always positive.

Note that we can always solve absolute value equations and inequalities graphically , as shown below.

Here are some problems:

Here’s one more that’s a bit tricky, since we have two expressions with absolute value in it. In this case, we have to separate in four cases , just to be sure we cover all the possibilities. We then must check for extraneous solutions , possible solutions that don’t work.

For example, when the expression $ 3x-2$ is negative, the absolute value of that expression is the negation of it, or $ -3x+2$, to make it positive in the equation. Play around with some numbers and you’ll see this!

When we get all the possible answers, check for extraneous solutions , since we’re dealing with absolute value. We found two answers that worked: $ \displaystyle x=\frac{3}{2}$ and $ x=-1$. You can also put the equation in your graphing calculator to check your answers!

Here’s another way to approach the absolute value problem above, using number lines :

Now draw number lines for each absolute value, and then for the whole equation above . We see for the last number line that for $ <-2$, we’ll use $ 2-3x$ and $ -x-2$, between $ -2$ and $ \displaystyle \frac{2}{3}$, we’ll use $ 2-3x$ and $ x+2$ , and $ \displaystyle >\frac{2}{3}$, we’ll use $ 3x-2$ and $ x+2$.

After solving for $ x$ in the original equation, we have to check to make sure each value we get for $ x$ falls into the correct interval of the number line. For example, $ \displaystyle -\frac{3}{2}$ isn’t  $ <-2$,  so we have to “throw it away”. $ -1$ is between $ -2$ and $ \displaystyle \frac{2}{3}$, so it works, and $ \displaystyle \frac{3}{2}$ is $ \displaystyle >\frac{2}{3}$, so it works.

We have $ \displaystyle x=\frac{3}{2}$ and $ x=-1$.   √

Solving Absolute Value Inequalities

Note that we learned about Linear Inequalities here .

When dealing with absolute values and inequalities (just like with absolute value equations), we have to separate the inequality into two different ones , if there are any variables inside the absolute value bars.

First, get the absolute value all by itself on the left (remember to reverse the inequality sign when multiplying or dividing by a negative number). Now, separate the equations. We get the first equation by just taking away the absolute value sign away on the left. The easiest way to get the second equation is to take the absolute value sign away on the left, and do two things on the right :  reverse the inequality sign , and change the sign of everything on the right (even if we have variables over there).

We also have to think about whether or not to use “ or ” or “ and ” between the two new equations. The way I remember this is that with a $ >\,\text{or}\,\,\ge  $ sign, you can remember “gore”: greater than uses “or” . With a  $ <\,\text{or}\,\,\le  $ sign, think “land”: less than uses “and” .

GORE: Greater Than ­­­uses OR LAND:  Less Than uses AND

Note that statement with “or” is a disjunction , which means that it works if only one (or both) parts are true. A statement with “and” is a conjunction , which means it only works if both parts are true.

And again, if we get something like $ \left| {x+3} \right|<0$ (or a negative number), there is no solution , and something like $ \left| {x+3} \right|\ge 0$ (or a negative number), there are infinite solutions (all real numbers).

Also, remember to use open brackets for inequalities that aren’t inclusive ($ <$ and $ <$) and closed brackets for inequalities that are inclusive and include the boundary point ($ \le $ and $ \ge $).

Here are some examples:

There are examples of rational functions with absolute values here in the Rational Functions, Equations, and Inequalities section .

Graphs of Absolute Value Functions

Note that you can put absolute values in your Graphing Calculator (and even graph them!) by hitting MATH, scroll right to NUM , and then hitting 1 (abs) or ENTER .

Absolute Value functions typically look like a V (upside down if the absolute value is negative), where the point at the V is called the vertex . For the absolute value parent function, the vertex is at $ \left( {0,0} \right)$.

We looked at absolute value parent functions and their transformations in the  Absolute Value Transformations  section , and absolute value functions as piecewise equations here in the Piecewise Functions section .

Note that the general form for the absolute value function is  $ f\left( x \right)=a\left| {x-h} \right|+k$, where $ \left( {h,k} \right)$ is the vertex. If $ a$ is positive, the function points down (like a V ); if $ a$ is negative, the function points up (like an upside-down V ). Here’s a graph of the parent function, and also a transformation:

Without using a t-chart, we can see that the vertex is at $ \left( {-2,1} \right)$ and the graph is upside-down because of the negative sign. It’s also stretched vertically by a factor of 3 and horizontal by a factor of $ \displaystyle \frac{1}{2}$ (or stretched vertically by a factor of 6 ); thus, other points down can be drawn by going back and forth 1 and down 6 .

You can solve absolute value equations and equalities with graphing ; here are some examples of solving inequalities:

Applications of Absolute Value Functions

Absolute Value Functions are in many applications , especially in those involving V-shaped paths and margin of errors , or tolerances . Here are some examples absolute value “word” problems that you may see:

Here are examples that are absolute value inequality applications . Use this rule of thumb : the absolute value of a difference is usually on the left-hand side, the amount that differs or varies is usually on the right-hand side, with a $ <$ or $ \le $ sign in between.

Learn these rules, and practice, practice, practice!

Click on Submit (the arrow to the right of the problem) to solve this problem. You can also type in more problems, or click on the 3 dots in the upper right hand corner to drill down for example problems.

If you click on “Tap to view steps”, you will go to the  Mathway  site, where you can register for the  full version  (steps included) of the software.  You can even get math worksheets.

You can also go to the  Mathway  site here , where you can register, or just use the software for free without the detailed solutions.  There is even a Mathway App for your mobile device.  Enjoy!

On to  Solving Radical Equations and Inequalities – you’re ready!

Module 3: Quadratic Equations and Functions

Equations and inequalities with absolute value, learning objectives.

• Solve equations containing absolute values
• Recognize when a linear equation that contains absolute value does not have a solution

Solve inequalities containing absolute values

Solving an absolute value equation.

Next, we will learn how to slve an absolute value equation . To solve an equation such as [latex]|2x - 6|=8[/latex], we notice that the absolute value will be equal to 8 if the quantity inside the absolute value bars is [latex]8[/latex] or [latex]-8[/latex]. This leads to two different equations we can solve independently.

Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.

A General Note: Absolute Value Equations

The absolute value of x is written as [latex]|x|[/latex]. It has the following properties:

For real numbers [latex]A[/latex] and [latex]B[/latex], an equation of the form [latex]|A|=B[/latex], with [latex]B\ge 0[/latex], will have solutions when [latex]A=B[/latex] or [latex]A=-B[/latex]. If [latex]B<0[/latex], the equation [latex]|A|=B[/latex] has no solution.

An absolute value equation in the form [latex]|ax+b|=c[/latex] has the following properties:

How To: Given an absolute value equation, solve it.

• Isolate the absolute value expression on one side of the equal sign.
• If [latex]c>0[/latex], write and solve two equations: [latex]ax+b=c[/latex] and [latex]ax+b=-c[/latex].

In the next video, we show examples of solving a simple absolute value equation.

Example: Solving Absolute Value Equations

Solve the following absolute value equations:

• [latex]|6x+4|=8[/latex]
• [latex]|3x+4|=-9[/latex]
• [latex]|3x - 5|-4=6[/latex]
• [latex]|-5x+10|=0[/latex]

Write two equations and solve each:

[latex]\begin{array}{ll}6x+4\hfill&=8\hfill& 6x+4\hfill&=-8\hfill \\ 6x\hfill&=4\hfill& 6x\hfill&=-12\hfill \\ x\hfill&=\frac{2}{3}\hfill& x\hfill&=-2\hfill \end{array}[/latex]

The two solutions are [latex]x=\frac{2}{3}[/latex], [latex]x=-2[/latex].

b. [latex]|3x+4|=-9[/latex]

There is no solution as an absolute value cannot be negative.

c. [latex]|3x - 5|-4=6[/latex]

Isolate the absolute value expression and then write two equations.

There are two solutions: [latex]x=5[/latex], [latex]x=-\frac{5}{3}[/latex].

d. [latex]|-5x+10|=0[/latex]

The equation is set equal to zero, so we have to write only one equation.

There is one solution: [latex]x=2[/latex].

In the two videos that follow, we show examples of how to solve an absolute value equation that requires you to isolate the absolute value first using mathematical operations.

Solve the absolute value equation: [latex]|1 - 4x|+8=13[/latex].

Absolute value equations with no solutions

As we are solving absolute value equations it is important to be aware of special cases. An absolute value is defined as the distance from 0 on a number line, so it must be a positive number. When an absolute value expression is equal to a negative number, we say the equation has no solution, or DNE. Notice how this happens in the next two examples.

Solve for x . [latex]7+\left|2x-5\right|=4[/latex]

[latex]\begin{array}{r}7+\left|2x-5\right|=4\,\,\,\,\\\underline{\,-7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-7\,}\\\left|2x-5\right|=-3\end{array}[/latex]

Result of absolute value is negative! The result of an absolute value must always be positive, so we say there is no solution to this equation, or DNE.

Solve for x . [latex]-\frac{1}{2}\left|x+3\right|=6[/latex]

[latex]\begin{array}{r}-\frac{1}{2}\left|x+3\right|=6\,\,\,\,\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\,\,\left(-2\right)-\frac{1}{2}\left|x+3\right|=\left(-2\right)6\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left|x+3\right|=-12\,\,\,\,\,\end{array}[/latex]

Again, we have a result where an absolute value is negative!

There is no solution to this equation, or DNE.

In this last video, we show more examples of absolute value equations that have no solutions.

Let’s apply what you know about solving equations that contain absolute values and what you know about inequalities to solve inequalities that contain absolute values. Let’s start with a simple inequality.

[latex]\left|x\right|\leq 4[/latex]

This inequality is read, “the absolute value of x is less than or equal to 4.” If you are asked to solve for x , you want to find out what values of x are 4 units or less away from 0 on a number line. You could start by thinking about the number line and what values of x would satisfy this equation.

4 and [latex]−4[/latex] are both four units away from 0, so they are solutions. 3 and [latex]−3[/latex] are also solutions because each of these values is less than 4 units away from 0. So are 1 and [latex]−1[/latex], 0.5 and [latex]−0.5[/latex], and so on—there are an infinite number of values for x that will satisfy this inequality.

The graph of this inequality will have two closed circles, at 4 and [latex]−4[/latex]. The distance between these two values on the number line is colored in blue because all of these values satisfy the inequality.

The solution can be written this way:

Inequality: [latex]-4\leq x\leq4[/latex]

Interval: [latex]\left[-4,4\right][/latex]

The situation is a little different when the inequality sign is “greater than” or “greater than or equal to.” Consider the simple inequality [latex]\left|x\right|>3[/latex]. Again, you could think of the number line and what values of x are greater than 3 units away from zero. This time, 3 and [latex]−3[/latex] are not included in the solution, so there are open circles on both of these values. 2 and [latex]−2[/latex] would not be solutions because they are not more than 3 units away from 0. But 5 and [latex]−5[/latex] would work, and so would all of the values extending to the left of [latex]−3[/latex] and to the right of 3. The graph would look like the one below.

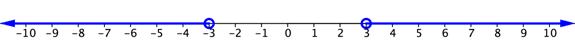
The solution to this inequality can be written this way:

Inequality : [latex]x<−3[/latex] or [latex]x>3[/latex].

Interval: [latex]\left(-\infty, -3\right)\cup\left(3,\infty\right)[/latex]

In the following video, you will see examples of how to solve and express the solution to absolute value inequalities involving both AND and OR.

Writing Solutions to Absolute Value Inequalities

For any positive value of a  and  x,  a single variable, or any algebraic expression:

Let’s look at a few more examples of inequalities containing absolute values.

Solve for x . [latex]\left|x+3\right|\gt4[/latex]

Since this is a “greater than” inequality, the solution can be rewritten according to the “greater than” rule.

[latex] \displaystyle x+3<-4\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,\,x+3>4[/latex]

Solve each inequality.

[latex]\begin{array}{r}x+3<-4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x+3>4\\\underline{\,\,\,\,-3\,\,\,\,\,-3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,-3\,\,-3}\\x\,\,\,\,\,\,\,\,\,<-7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,>1\\\\x<-7\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,x>1\,\,\,\,\,\,\,\end{array}[/latex]

Check the solutions in the original equation to be sure they work. Check the end point of the first related equation, [latex]−7[/latex] and the end point of the second related equation, 1.

[latex] \displaystyle \begin{array}{r}\,\,\,\left| x+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x+3 \right|>4\\\left| -7+3 \right|=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 1+3 \right|=4\\\,\,\,\,\,\,\,\left| -4 \right|=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 4 \right|=4\\\,\,\,\,\,\,\,\,\,\,\,\,4=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4=4\end{array}[/latex]

Try [latex]−10[/latex], a value less than [latex]−7[/latex], and 5, a value greater than 1, to check the inequality.

[latex] \displaystyle \begin{array}{r}\,\,\,\,\,\left| x+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x+3 \right|>4\\\left| -10+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 5+3 \right|>4\\\,\,\,\,\,\,\,\,\,\,\left| -7 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 8 \right|>4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,7>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,8>4\end{array}[/latex]

Both solutions check!

Inequality: [latex] \displaystyle x<-7\,\,\,\,\,\text{or}\,\,\,\,\,x>1[/latex]

Interval: [latex]\left(-\infty, -7\right)\cup\left(1,\infty\right)[/latex]

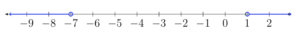
Solve for y.  [latex] \displaystyle \mathsf{3}\left| \mathsf{2}\mathrm{y}\mathsf{+6} \right|-\mathsf{9<27}[/latex]

Begin to isolate the absolute value by adding 9 to both sides of the inequality.

[latex] \displaystyle \begin{array}{r}3\left| 2y+6 \right|-9<27\\\underline{\,\,+9\,\,\,+9}\\3\left| 2y+6 \right|\,\,\,\,\,\,\,\,<36\end{array}[/latex]

Divide both sides by 3 to isolate the absolute value.

[latex]\begin{array}{r}\underline{3\left| 2y+6 \right|}\,<\underline{36}\\3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\,\\\,\,\,\,\,\,\,\,\,\left| 2y+6 \right|<12\end{array}[/latex]

Write the absolute value inequality using the “less than” rule. Subtract 6 from each part of the inequality.

[latex]\begin{array}{r}-12<2y+6<12\\\underline{\,\,-6\,\,\,\,\,\,\,\,\,\,\,\,\,-6\,\,\,-6}\\-18\,<\,2y\,\,\,\,\,\,\,\,\,<\,\,6\,\end{array}[/latex]

Divide by 2 to isolate the variable.

[latex]\begin{array}{r}\underline{-18}<\underline{2y}<\underline{\,6\,}\\2\,\,\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,2\,\,\\-9<\,\,y\,\,\,\,<\,3\end{array}[/latex]

Inequality: [latex] \displaystyle -9<\,\,y\,\,<3[/latex]

Interval: [latex]\left(-9,3\right)[/latex]

Identify cases of inequalities containing absolute values that have no solutions

As with equations, there may be instances in which there is no solution to an inequality.

Solve for x. [latex]\left|2x+3\right|+9\leq 7[/latex]

Isolate the absolute value by subtracting 9 from both sides of the inequality.

[latex] \displaystyle \begin{array}{r}\left| 2x+3 \right|+9\,\le \,\,\,7\,\,\\\underline{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-9\,\,\,\,\,-9}\\\,\,\,\,\,\,\,\left| 2x+3 \right|\,\,\,\le -2\,\end{array}[/latex]

The absolute value of a quantity can never be a negative number, so there is no solution to the inequality.

No solution

Absolute inequalities can be solved by rewriting them using compound inequalities. The first step to solving absolute inequalities is to isolate the absolute value. The next step is to decide whether you are working with an OR inequality or an AND inequality. If the inequality is greater than a number, we will use OR. If the inequality is less than a number, we will use AND. Remember that if we end up with an absolute value greater than or less than a negative number, there is no solution.

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Ex 1: Solve and Graph Basic Absolute Value inequalities.. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/0cXxATY2S-k . License : CC BY: Attribution
• Ex 2: Solve and Graph Absolute Value inequalities . Authored by : James Sousa (Mathispower4u.com) . Located at : . License : CC BY: Attribution
• Ex 4: Solve and Graph Absolute Value inequalities (Requires Isolating Abs. Value).. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/5jRUuiMUxWQ . License : CC BY: Attribution
• College Algebra. . Authored by : Abramson, et al... Provided by : OpenStax. Located at : . License : CC BY: Attribution . License Terms : Download for free: http://cnx.org/contents/[email protected]:1/Preface
• Ex 4: Solving Absolute Value Equations (Requires Isolating Abs. Value).. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : . License : CC BY: Attribution
• Question ID 60839. Authored by : Alyson Day. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL

Privacy Policy

Chapter 2 Equations and Inequalities

2.6 Linear Inequalities and Absolute Value Inequalities

Learning objectives.

In this section, you will:

• Write solutions using interval notation.
• Solve inequalities in one variable algebraically.
• Solve absolute value inequalities.

It is not easy to make the honor role at most top universities. Suppose students were required to carry a course load of at least 12 credit hours and maintain a grade point average of 3.5 or above. How could these honor roll requirements be expressed mathematically? In this section, we will explore various ways to express different sets of numbers, inequalities, and absolute value inequalities.

Write Solutions Using Interval Notation

Indicating the solution to an inequality such as[latex]\,x\ge 4\,[/latex]can be achieved in several ways.

We can use a number line as shown in Figure 2 . The blue ray begins at[latex]\,x=4\,[/latex]and, as indicated by the arrowhead, continues to infinity, which illustrates that the solution set includes all real numbers greater than or equal to 4.

We can use set-builder notation :[latex]\,\left\{x|x\ge 4\right\},[/latex] which translates to “all real numbers x such that x is greater than or equal to 4.” Notice that braces are used to indicate a set.

The third method is interval notation, in which solution sets are indicated with parentheses or brackets. The solutions to[latex]\,x\ge 4\,[/latex]are represented as[latex]\,\left[4,\infty \right).\,[/latex]This is perhaps the most useful method, as it applies to concepts studied later in this course and to other higher-level math courses.

The main concept to remember is that parentheses represent solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be “equaled.” A few examples of an interval, or a set of numbers in which a solution falls, are[latex]\,\left[-2,6\right),[/latex] or all numbers between[latex]\,-2\,[/latex]and[latex]\,6,[/latex] including[latex]\,-2,[/latex] but not including[latex]\,6;[/latex][latex]\left(-1,0\right),[/latex]all real numbers between, but not including[latex]\,-1\,[/latex]and[latex]\,0;[/latex]and[latex]\,\left(-\infty ,1\right],[/latex] all real numbers less than and including[latex]\,1.\,[/latex] The Table 1 below outlines the possibilities.

Using Interval Notation to Express All Real Numbers Greater Than or Equal to a

Use interval notation to indicate all real numbers greater than or equal to[latex]\,-2.[/latex]

Use a bracket on the left of[latex]\,-2\,[/latex]and parentheses after infinity:[latex]\,\left[-2,\infty \right).[/latex]The bracket indicates that[latex]\,-2\,[/latex]is included in the set with all real numbers greater than[latex]\,-2\,[/latex]to infinity.

Use interval notation to indicate all real numbers between and including[latex]\,-3\,[/latex]and[latex]\,5.[/latex]

[latex]\left[-3,5\right][/latex]

Using Interval Notation to Express All Real Numbers Less Than or Equal to a or Greater Than or Equal to b

Write the interval expressing all real numbers less than or equal to[latex]\,-1\,[/latex]or greater than or equal to[latex]\,1.[/latex]

We have to write two intervals for this example. The first interval must indicate all real numbers less than or equal to 1. So, this interval begins at[latex]\,-\infty \,[/latex]and ends at[latex]\,-1,[/latex]which is written as[latex]\,\left(-\infty ,-1\right].[/latex]

The second interval must show all real numbers greater than or equal to[latex]\,1,[/latex]which is written as[latex]\,\left[1,\infty \right).\,[/latex]However, we want to combine these two sets. We accomplish this by inserting the union symbol,[latex]\cup ,[/latex]between the two intervals.

Express all real numbers less than[latex]\,-2\,[/latex]or greater than or equal to 3 in interval notation.

[latex]\left(-\infty ,-2\right)\cup \left[3,\infty \right)[/latex]

Solving Inequalities in One Variable Algebraically

Using the properties of inequalities.

When we work with inequalities, we can usually treat them similarly to but not exactly as we treat equalities. We can use the addition property and the multiplication property to help us solve them. The one exception is when we multiply or divide by a negative number; doing so reverses the inequality symbol.

Properties of Inequalities

These properties also apply to[latex]\,a\le b,[/latex][latex]a \gt b,[/latex] and[latex]\,a\ge b.[/latex]

Demonstrating the Addition Property

Illustrate the addition property for inequalities by solving each of the following:

(a) [latex]x-15\lt 4[/latex]

(b) [latex]6\ge x-1[/latex]

(c) [latex]x+7\gt 9[/latex]

The addition property for inequalities states that if an inequality exists, adding or subtracting the same number on both sides does not change the inequality.

• [latex]\begin{array}{ll}\phantom{\rule{2em}{0ex}}x-15\lt 4\hfill & \hfill \\ x-15+15\lt 4+15 \hfill & \phantom{\rule{2em}{0ex}}\text{Add 15 to both sides}.\hfill \\ \phantom{\rule{4em}{0ex}}x \lt 19\hfill & \hfill \end{array}[/latex]
• [latex]\begin{array}{ll}\phantom{\rule{2em}{0ex}}6\ge x-1\hfill & \hfill \\ 6+1\ge x-1+1\hfill & \phantom{\rule{4em}{0ex}}\text{Add 1 to both sides}.\hfill \\ \phantom{\rule{2em}{0ex}}7\ge x\hfill & \hfill \end{array}[/latex]
• [latex]\begin{array}{ll}\phantom{\rule{2em}{0ex}}x+7\gt 9\hfill & \hfill \\ x+7-7>9-7\hfill & \phantom{\rule{4em}{0ex}}\text{Subtract 7 from both sides}.\hfill \\ \phantom{\rule{3em}{0ex}}x\gt 2\hfill & \hfill \end{array}[/latex]

Solve:[latex]\,3x-2 \lt 1.[/latex]

[latex]x \lt 1[/latex]

Demonstrating the Multiplication Property

Illustrate the multiplication property for inequalities by solving each of the following:

• [latex]3x\lt 6[/latex]
• [latex]-2x-1\ge 5[/latex]
• [latex]5-x>10[/latex]
• [latex]\begin{array}{l}\phantom{\rule{1.5em}{0ex}}3x\lt 6\hfill \\ \frac{1}{3}\left(3x\right)\lt \left(6\right)\frac{1}{3}\hfill \\ \phantom{\rule{2em}{0ex}}x\lt 2\hfill \end{array}[/latex]
• [latex]\begin{array}{ll}\phantom{\rule{1em}{0ex}}-2x-1\ge 5\hfill & \hfill \\ \phantom{\rule{3em}{0ex}}-2x\ge 6\hfill & \hfill \\ \left(-\frac{1}{2}\right)\left(-2x\right)\ge \left(6\right)\left(-\frac{1}{2}\right)\hfill & \phantom{\rule{2em}{0ex}}\text{Multiply by }-\frac{1}{2}.\hfill \\ \phantom{\rule{4em}{0ex}}x\le -3\hfill & \phantom{\rule{2em}{0ex}}\text{Reverse the inequality}.\hfill \end{array}[/latex]
• [latex]\begin{array}{ll}\phantom{\rule{2.5em}{0ex}}5-x>10\hfill & \hfill \\ \phantom{\rule{3.5em}{0ex}}-x>5\hfill & \hfill \\ \left(-1\right)\left(-x\right)>\left(5\right)\left(-1\right)\hfill & \phantom{\rule{2em}{0ex}}\text{Multiply by }-1.\hfill \\ \phantom{\rule{4.5em}{0ex}}x\lt -5\hfill & \phantom{\rule{2em}{0ex}}\text{Reverse the inequality}.\hfill \end{array}[/latex]

Solve:[latex]\,4x+7\ge 2x-3.[/latex]

[latex]x\ge -5[/latex]

As the examples have shown, we can perform the same operations on both sides of an inequality, just as we do with equations; we combine like terms and perform operations. To solve, we isolate the variable.

Solving an Inequality Algebraically

Solve the inequality: 13 – 7x [latex]\geq[/latex] 10x – 4

Solving this inequality is similar to solving an equation up until the last step.

The solution set is given by the interval[latex]\,\left(-\infty ,1\right],[/latex] or all real numbers less than and including 1.

Solve the inequality and write the answer using interval notation:[latex]\,-x+4\lt\frac{1}{2}x+1.[/latex]

[latex]\left(2,\infty \right)[/latex]

Solving an Inequality with Fractions

Solve the following inequality and write the answer in interval notation:

–[latex]\dfrac{3}{4}[/latex] x    [latex]\geq[/latex]  – [latex]\dfrac{5}{8}[/latex]  + [latex]\dfrac{2}{3}[/latex] x

We begin solving in the same way we do when solving an equation.

Solve the inequality and write the answer in interval notation:[latex]\,-\frac{5}{6}x\le \frac{3}{4}+\frac{8}{3}x.[/latex]

[latex]\left[-\frac{3}{14},\infty \right)[/latex]

Understanding Compound Inequalities

A compound inequality includes two inequalities in one statement. A statement such as[latex]\,4\lt x\le 6\,[/latex]means[latex]\,4 \lt x\,[/latex]and[latex]\,x\le 6.\,[/latex]There are two ways to solve compound inequalities: separating them into two separate inequalities or leaving the compound inequality intact and performing operations on all three parts at the same time. We will illustrate both methods.

Solving a Compound Inequality

Solve the compound inequality: 3 [latex]\leq[/latex] 2 x + 2 [latex]\lt 6[/latex]

The first method is to write two separate inequalities: 3 [latex]\leq[/latex] 2 x + 2 and 2 x + 2 [latex]\lt 6[/latex].  We solve them independently.

Then, we can rewrite the solution as a compound inequality, the same way the problem began.

[latex]\dfrac{1}{2}[/latex] [latex]\leq[/latex] x  [latex]\lt[/latex]  2

In interval notation, the solution is written as [ [latex]\dfrac{1}{2}[/latex], 2).

The second method is to leave the compound inequality intact and perform solving procedures on the three parts at the same time.

We get the same solution: [ [latex]\dfrac{1}{2}[/latex], 2).

Solve the compound inequality:[latex]\,4\lt 2x-8\le 10.[/latex]

[latex]6\lt x\le 9\text{​}\text{​}\,\,\text{or}\,\,\left(6,9\right][/latex]

Solving a Compound Inequality with the Variable in All Three Parts

Solve the compound inequality with variables in all three parts:[latex]\,3+x>7x-2>5x-10.[/latex]

Let’s try the first method. Write two inequalities:

The solution set is[latex]\,-4\lt x\lt\frac{5}{6}\,[/latex]or in interval notation[latex]\,\left(-4,\frac{5}{6}\right).\,[/latex]Notice that when we write the solution in interval notation, the smaller number comes first. We read intervals from left to right, as they appear on a number line. See Figure 3.

Solve the compound inequality:[latex]\,3y\lt 4-5y\lt 5+3y.[/latex]

[latex]\left(-\frac{1}{8},\frac{1}{2}\right)[/latex]

Solving Absolute Value Inequalities

As we know, the absolute value of a quantity is a positive number or zero. From the origin, a point located at[latex]\,\left(-x,0\right)\,[/latex]has an absolute value of[latex]\,x,[/latex] as it is x units away. Consider absolute value the distance from one point to another point. Regardless of direction, positive or negative, the distance between the two points is represented as a positive number or zero.

An absolute value inequality is an equation of the form

where A , and sometimes B , represents an algebraic expression dependent on a variable x. Solving the inequality means finding the set of all [latex]\,x[/latex] – values that satisfy the problem. Usually this set will be an interval or the union of two intervals and will include a range of values.

There are two basic approaches to solving absolute value inequalities: graphical and algebraic. The advantage of the graphical approach is we can read the solution by interpreting the graphs of two equations. The advantage of the algebraic approach is that solutions are exact, as precise solutions are sometimes difficult to read from a graph.

Suppose we want to know all possible returns on an investment if we could earn some amount of money within $200 of $600. We can solve algebraically for the set of x- values such that the distance between[latex]\,x\,[/latex]and 600 is less than 200. We represent the distance between[latex]\,x\,[/latex]and 600 as[latex]\,|x-600|,[/latex] and therefore,[latex]\,|x-600|\le 200\,[/latex]or

This means our returns would be between $400 and $800.

To solve absolute value inequalities, just as with absolute value equations, we write two inequalities and then solve them independently.

Absolute Value Inequalities

For an algebraic expression X, and[latex]\,k>0,[/latex] an absolute value inequality is an inequality of the form

These statements also apply to[latex]\,|X|\le k\,[/latex]and[latex]\,|X|\ge k.[/latex]

Determining a Number within a Prescribed Distance

Describe all values[latex]\,x\,[/latex]within a distance of 4 from the number 5.

We want the distance between[latex]\,x\,[/latex]and 5 to be less than or equal to 4. We can draw a number line, such as in Figure 4 , to represent the condition to be satisfied.

The distance from[latex]\,x\,[/latex]to 5 can be represented using an absolute value symbol,[latex]\,|x-5|.\,[/latex]Write the values of[latex]\,x\,[/latex]that satisfy the condition as an absolute value inequality.

We need to write two inequalities, as there are always two solutions to an absolute value equation.

If the solution set is[latex]\,x\le 9\,[/latex]and[latex]\,x\ge 1,[/latex] then the solution set is an interval including all real numbers between and including 1 and 9.

So[latex]\,|x-5|\le 4\,[/latex]is equivalent to[latex]\,\left[1,9\right]\,[/latex]in interval notation.

Describe all x- values within a distance of 3 from the number 2.

[latex]|x-2|\le 3[/latex]

Solving an Absolute Value Inequality

Solve [latex]|x-1|\le 3[/latex].

Using a Graphical Approach to Solve Absolute Value Inequalities

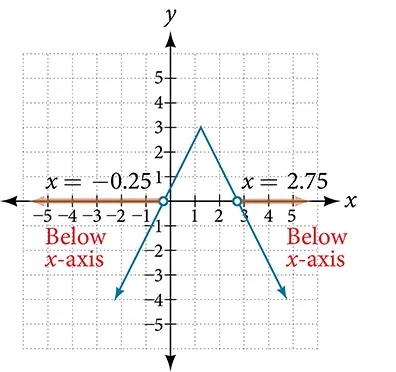
Given the equation [latex]y=-\frac{1}{2}|4x-5|+3,[/latex] determine the x -values for which the y -values are negative.

We are trying to determine where[latex]\,y\lt0,[/latex] which is when[latex]\,-\frac{1}{2}|4x-5|+30.\,[/latex]We begin by isolating the absolute value.

[latex]-\frac{1}{2}[/latex] |4x-5| [latex]\lt[/latex] – 3      Multiply both sides by -2 and reverse the inequality.

|4x-5| [latex]\gt[/latex] 6

Next, we solve for the equality [latex]|4x-5|=6.[/latex]

Now, we can examine the graph to observe where the y- values are negative. We observe where the branches are below the x- axis. Notice that it is not important exactly what the graph looks like, as long as we know that it crosses the horizontal axis at[latex]\,x=-\frac{1}{4}\,[/latex]and[latex]\,x=\frac{11}{4}[/latex] and that the graph opens downward. See Figure 5.

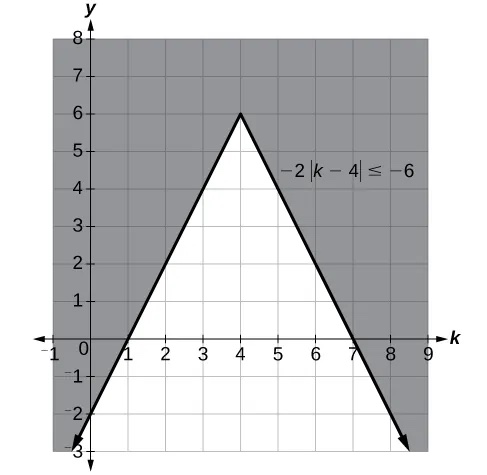
Solve[latex]\,-2|k-4|\le -6.[/latex]

[latex]k\le 1\,[/latex]or[latex]\,k\ge 7;[/latex] in interval notation, this would be[latex]\,\left(-\infty ,1\right]\cup \left[7,\infty \right).[/latex]

Key Concepts

• Interval notation is a method to indicate the solution set to an inequality. Highly applicable in calculus, it is a system of parentheses and brackets that indicate what numbers are included in a set and whether the endpoints are included as well.
• Solving inequalities is similar to solving equations. The same algebraic rules apply, except for one: multiplying or dividing by a negative number reverses the inequality.
• Compound inequalities often have three parts and can be rewritten as two independent inequalities. Solutions are given by boundary values, which are indicated as a beginning boundary or an ending boundary in the solutions to the two inequalities.
• Absolute value inequalities will produce two solution sets due to the nature of absolute value. We solve by writing two equations: one equal to a positive value and one equal to a negative value.
• Absolute value inequalities can also be solved by graphing. At least we can check the algebraic solutions by graphing, as we cannot depend on a visual for a precise solution.

Section Exercises

• When solving an inequality, explain what happened from Step 1 to Step 2:

[latex]\begin{array}{ll}\text{Step 1}\hfill & \phantom{\rule{2em}{0ex}}-2x\gt 6\hfill \\ \text{Step 2}\hfill & \phantom{\rule{3em}{0ex}}x\lt -3\hfill \end{array}[/latex]

When we divide both sides by a negative it changes the sign of both sides so the sense of the inequality sign changes.

• When solving an inequality, we arrive at:

[latex]\begin{array}{l}x+2\lt x+3\hfill \\ \phantom{\rule{1.2em}{0ex}}2 \lt 3\hfill \end{array}[/latex]

Explain what our solution set is.

• When writing our solution in interval notation, how do we represent all the real numbers?

[latex]\left(-\infty ,\infty \right)[/latex]

[latex]\begin{array}{l}x+2>x+3\hfill \\ \phantom{\rule{1.2em}{0ex}}2>3\hfill \end{array}[/latex]

• Describe how to graph[latex]\,y=|x-3|[/latex]

We start by finding the x -intercept, or where the function = 0. Once we have that point, which is[latex]\,\left(3,0\right),[/latex] we graph to the right the straight line graph[latex]\,y=x-3,[/latex] and then when we draw it to the left we plot positive y values, taking the absolute value of them.

For the following exercises, solve the inequality. Write your final answer in interval notation.

• [latex]4x-7\le 9[/latex]
• [latex]3x+2\ge 7x-1[/latex]

[latex]\left(-\infty ,\frac{3}{4}\right][/latex]

• [latex]-2x+3>x-5[/latex]
• [latex]4\left(x+3\right)\ge 2x-1[/latex]

[latex]\left[\frac{-13}{2},\infty \right)[/latex]

• [latex]-\frac{1}{2}x\le \frac{-5}{4}+\frac{2}{5}x[/latex]
• [latex]-5\left(x-1\right)+3>3x-4-4x[/latex]

[latex]\left(-\infty ,3\right)[/latex]

• [latex]-3\left(2x+1\right)>-2\left(x+4\right)[/latex]
• [latex]\frac{x+3}{8}-\frac{x+5}{5}\ge \frac{3}{10}[/latex]

[latex]\left(-\infty ,-\frac{37}{3}\right][/latex]

• [latex]\frac{x-1}{3}+\frac{x+2}{5}\le \frac{3}{5}[/latex]

For the following exercises, solve the inequality involving absolute value. Write your final answer in interval notation.

• [latex]|x+9|\ge -6[/latex]

All real numbers[latex]\,\left(-\infty ,\infty \right)[/latex]

• [latex]|2x+3|\lt 7[/latex]
• [latex]|3x-1|>11[/latex]

[latex]\left(-\infty ,\frac{-10}{3}\right)\cup \left(4,\infty \right)[/latex]

• [latex]|2x+1|+1\le 6[/latex]
• [latex]|x-2|+4\ge 10[/latex]

[latex]\left(-\infty ,-4\right]\cup \left[8,+\infty \right)[/latex]

• [latex]|-2x+7|\le 13[/latex]
• [latex]|x-7|\lt-4[/latex]

No solution

• [latex]|x-20|>-1[/latex]
• [latex]|\frac{x-3}{4}|\lt 2[/latex]

[latex]\left(-5,11\right)[/latex]

For the following exercises, describe all the x -values within or including a distance of the given values.

• Distance of 5 units from the number 7
• Distance of 3 units from the number 9

[latex]\left[6,12\right][/latex]

• Distance of10 units from the number 4
• Distance of 11 units from the number 1

[latex]\left[-10,12\right][/latex]

For the following exercises, solve the compound inequality. Express your answer using inequality signs, and then write your answer using interval notation.

• [latex]-4\lt 3x+2\le 18[/latex]
• [latex]3x+1>2x-5>x-7[/latex]

[latex]\begin{array}{ll}x>-6\text{ and }x>-2\hfill & \phantom{\rule{2em}{0ex}}\text{Take the intersection of two sets}.\hfill \\ x>-2,\text{ }\left(-2,+\infty \right)\hfill & \hfill \end{array}[/latex]

• [latex]3y\lt 5-2y\lt 7+y[/latex]
• [latex]2x-5-11\text{ or }5x+1\ge 6[/latex]

[latex]\begin{array}{ll}x-3\text{ }\mathrm{or}\text{ }x\ge 1\hfill & \phantom{\rule{2em}{0ex}}\text{Take the union of the two sets}.\hfill \\ \left(-\infty ,-3\right){{\cup }^{\text{​}}}^{\text{​}}\left[1,\infty \right)\hfill & \hfill \end{array}[/latex]

• [latex]x+7\lt x+2[/latex]

For the following exercises, write the set in interval notation.

• [latex]\left\{x|-1\lt x\lt 3\right\}[/latex]

[latex]\left(-1,3\right)[/latex]

• [latex]\left\{x|x\ge 7\right\}[/latex]
• [latex]\left\{x|x\lt 4\right\}[/latex]

[latex]\left(-\infty ,4\right)[/latex]

• [latex]\left\{\,x|\,x\text{ is all real numbers}\right\}[/latex]

For the following exercises, write the interval in set-builder notation.

• [latex]\left(-\infty ,6\right)[/latex]

[latex]\left\{x|x\lt 6\right\}[/latex]

• [latex]\left(4,+\infty \right)[/latex]
• [latex]\left[-3,5\right)[/latex]

[latex]\left\{x|-3\le x5\right\}[/latex]

• [latex]\left[-4,1\right]\cup \left[9,\infty \right)[/latex]

For the following exercises, write the set of numbers represented on the number line in interval notation.

[latex]\left(-2,1\right][/latex]

[latex]\left(-\infty ,4\right][/latex]

For the following exercises, input the left-hand side of the inequality as a Y1 graph in your graphing utility. Enter y2 = the right-hand side. Entering the absolute value of an expression is found in the MATH menu, Num, 1:abs(. Find the points of intersection, recall (2 nd CALC 5:intersection, 1 st curve, enter, 2 nd curve, enter, guess, enter). Copy a sketch of the graph and shade the x -axis for your solution set to the inequality. Write final answers in interval notation.

• [latex]|x+2|-5\lt 2[/latex]
• [latex]\frac{-1}{2}|x+2|\lt 4[/latex]

Where the blue is below the orange; always. All real numbers.[latex]\,\left(-\infty ,+\infty \right).[/latex]

• [latex]|4x+1|-3>2[/latex]
• [latex]|x-4|\lt 3[/latex]

Where the blue is below the orange;[latex]\,\left(1,7\right).[/latex]

• [latex]|x+2|\ge 5[/latex]
• Solve[latex]\,|3x+1|=|2x+3|[/latex]

[latex]x=2,\frac{-4}{5}[/latex]

• Solve[latex]{x}^{2}-x>12[/latex]
• [latex]\frac{x-5}{x+7}\le 0,[/latex][latex]x\ne -7[/latex]

[latex]\left(-7,5\right][/latex]

• [latex]p=-{x}^{2}+130x-3000\,[/latex]is a profit formula for a small business. Find the set of x -values that will keep this profit positive.

Real-World Applications

• In chemistry, the volume for a certain gas is given by[latex]\,V=20T,[/latex] where V is measured in cc and T is temperature in ºC. If the temperature varies between 80ºC and 120ºC, find the set of volume values.

[latex]\begin{array}{l}80\le T\le 120\\ 1,600\le 20T\le 2,400\end{array}[/latex]

[latex]\left[1,600, 2,400\right][/latex]

• A basic cellular package costs $20/mo. for 60 min of calling, with an additional charge of $.30/min beyond that time.. The cost formula would be[latex]\,C=\text{\$}20+.30\left(x-60\right).\,[/latex]If you have to keep your bill lower than $50, what is the maximum calling minutes you can use?

Media Attributions

• 2.6 Figure 1 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 2.6 Figure 2 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 2.6 Figure 3 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 2.6 Figure 4 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 2.6 Figure 5 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 2.6 Solution © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 2.6 Exercises #41 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 2.6 Exercises #42 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 2.6 Exercises #43 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 2.6 Exercises #45 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
• 2.6 Exercises #47 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license

College Algebra Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8: Linear Inequalities and Absolute Value Inequalities

• Last updated
• Save as PDF
• Page ID 1489

Learning Objectives

• Use interval notation.
• Use properties of inequalities.
• Solve inequalities in one variable algebraically.
• Solve absolute value inequalities.

It is not easy to make the honor role at most top universities. Suppose students were required to carry a course load of at least \(12\) credit hours and maintain a grade point average of \(3.5\) or above. How could these honor roll requirements be expressed mathematically? In this section, we will explore various ways to express different sets of numbers, inequalities, and absolute value inequalities.

Using Interval Notation

Indicating the solution to an inequality such as \(x≥4\) can be achieved in several ways.

• We can use a number line as shown in Figure \(\PageIndex{2}\). The blue ray begins at \(x = 4\) and, as indicated by the arrowhead, continues to infinity, which illustrates that the solution set includes all real numbers greater than or equal to \(4\).
• We can use set-builder notation : \(\{x|x≥4\}\), which translates to “all real numbers \(x\) such that \(x\) is greater than or equal to \(4\).” Notice that braces are used to indicate a set.
• The third method is interval notation , in which solution sets are indicated with parentheses or brackets. The solutions to \(x≥4\) are represented as \([4,\infty)\). This is perhaps the most useful method, as it applies to concepts studied later in this course and to other higher-level math courses.

The main concept to remember is that parentheses represent solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be “equaled.” A few examples of an interval, or a set of numbers in which a solution falls, are \([−2,6)\), or all numbers between \(−2\) and \(6\), including \(−2\), but not including \(6\); \((−1,0)\), all real numbers between, but not including \(−1\) and \(0\); and \((−\infty,1]\), all real numbers less than and including \(1\). Table \(\PageIndex{1}\) outlines the possibilities.

Example \(\PageIndex{1}\): Using Interval Notation to Express All Real Numbers Greater Than or Equal to a

Use interval notation to indicate all real numbers greater than or equal to \(−2\).

Use a bracket on the left of \(−2\) and parentheses after infinity: \([−2,\infty)\). The bracket indicates that \(−2\) is included in the set with all real numbers greater than \(−2\) to infinity.

Try It! \(\PageIndex{1}\)

Use interval notation to indicate all real numbers between and including \(−3\) and \(5\).

\([−3,5]\)

Example \(\PageIndex{2}\): Using Interval Notation to Express All Real Numbers Less Than or Equal to a or Greater Than or Equal to b

Write the interval expressing all real numbers less than or equal to \(−1\) or greater than or equal to \(1\).

We have to write two intervals for this example. The first interval must indicate all real numbers less than or equal to \(1\). So, this interval begins at \(−\infty\) and ends at \(−1\), which is written as \((−\infty,−1]\).

The second interval must show all real numbers greater than or equal to \(1\), which is written as \([1,\infty)\). However, we want to combine these two sets. We accomplish this by inserting the union symbol, ∪, between the two intervals.

\[(−\infty,−1]\cup[1,\infty) \nonumber\]

Try It! \(\PageIndex{2}\)

Express all real numbers less than \(−2\) or greater than or equal to \(3\) in interval notation.

\((−\infty,−2)\cup[3,\infty)\)

Using the Properties of Inequalities

When we work with inequalities, we can usually treat them similarly to but not exactly as we treat equalities. We can use the addition property and the multiplication property to help us solve them. The one exception is when we multiply or divide by a negative number; doing so reverses the inequality symbol.

PROPERTIES OF INEQUALITIES

Addition Property

• If \(a<b\), then \(a+c<b+c\).

Multiplication Property

• If \(a<b\) and \(c>0\), then \(ac<bc\).
• If \(a<b\) and \(c<0\), then \(ac>bc\).

These properties also apply to \(a≤b\), \(a>b\), and \(a≥b\).

Example \(\PageIndex{3}\): Demonstrating the Addition Property

Illustrate the addition property for inequalities by solving each of the following:

• (a) \(x−15<4\)
• (b) \(6≥x−1\)
• (c) \(x+7>9\)

The addition property for inequalities states that if an inequality exists, adding or subtracting the same number on both sides does not change the inequality.

\[\begin{align*} x-15&< 4\\ x-15+15&< 4+15\\ x&< 19 \end{align*}\]

\[\begin{align*} 6&\geq x-1\\ 6+1&\geq x-1+1\\ 7&\geq x \end{align*}\]

\[\begin{align*} x+7&> 9\\ x+7-7&> 9-7\\ x&> 2 \end{align*}\]

Try It! \(\PageIndex{3}\)

Solve: \(3x−2<1\).

Example \(\PageIndex{4}\): Demonstrating the Multiplication Property

Illustrate the multiplication property for inequalities by solving each of the following:

• \(3x<6\)
• \(−2x−1≥5\)
• \(5−x>10\)

\[\begin{align*} 3x&< 6\\ \dfrac{1}{3}(3x)&< (6)\dfrac{1}{3}\\ x&< 2 \end{align*}\]

\[\begin{align*} -2x-1&\geq 5\\ -2x&\geq 6\\ \left (-\dfrac{1}{2} \right )(-2)&\geq (6)\left (-\dfrac{1}{2} \right ) & & \text{Multiply by } \left (-\dfrac{1}{2} \right )\\ x&\leq -3 & & \text{Reverse the inequality.} \end{align*}\]

\[\begin{align*} 5-x&> 10\\ -x&> 5\\ (-1)(-x)&> (5)(-1) & & \text{Multiply by } -1\\ x&< -5 & & \text{Reverse the inequality.} \end{align*}\]

Try It! \(\PageIndex{4}\)

Solve: \(4x+7≥2x−3\).

\(x≥−5\)

Solving Inequalities in One Variable Algebraically

As the examples have shown, we can perform the same operations on both sides of an inequality, just as we do with equations; we combine like terms and perform operations. To solve, we isolate the variable.

Example \(\PageIndex{5}\): Solving an Inequality Algebraically

Solve the inequality: \(13−7x≥10x−4\).

Solving this inequality is similar to solving an equation up until the last step.

\[\begin{align*} 13-7x&\geq 10x-4\\ 13-17x&\geq -4 & & \text{Move variable terms to one side of the inequality}\\ -17x&\geq -17 & & \text{Isolate the variable term}\\ x&\leq 1 & & \text{Dividing both sides by -17 reverses the inequality.} \end{align*}\]

The solution set is given by the interval \((−\infty,1]\), or all real numbers less than and including \(1\).

Try It! \(\PageIndex{5}\)

Solve the inequality and write the answer using interval notation: \(−x+4<\dfrac{1}{2}x+1\).

\((2,\infty)\)

Example \(\PageIndex{6}\): Solving an Inequality with Fractions

Solve the following inequality and write the answer in interval notation: \(−\dfrac{3}{4}x≥−\dfrac{5}{8}+\dfrac{2}{3}x\).

We begin solving in the same way we do when solving an equation.

\[\begin{align*} -\dfrac{3}{4}x&\geq -\dfrac{5}{8}+\dfrac{2}{3}x\\[5pt] -\dfrac{3}{4}x-\dfrac{2}{3}x&\geq -\dfrac{5}{8} & & \text{Put variable terms on one side.}\\[5pt] -\dfrac{9}{12}x-\dfrac{8}{12}x&\geq -\dfrac{5}{8} & & \text{Write fractions with common denominator.}\\[5pt] -\dfrac{17}{12}x&\geq -\dfrac{5}{8}\\[5pt] x&\leq -\dfrac{5}{8}\left (-\dfrac{12}{17} \right ) & & \text{Multiplying by a negative number reverses the inequality.}\\[5pt] x&\leq \dfrac{15}{34} \end{align*}\]

The solution set is the interval \(\left (−\infty,\dfrac{15}{34} \right ]\).

Try It! \(\PageIndex{6}\)

Solve the inequality and write the answer in interval notation: \(−\dfrac{5}{6}x≤\dfrac{3}{4}+\dfrac{8}{3}x\).

\(\left [-\dfrac{3}{14},\infty \right )\)

Understanding Compound Inequalities

A compound inequality includes two inequalities in one statement. A statement such as \(4<x≤6\) means \(4<x\) and \(x≤6.\) There are two ways to solve compound inequalities: separating them into two separate inequalities or leaving the compound inequality intact and performing operations on all three parts at the same time. We will illustrate both methods.

Example \(\PageIndex{7}\): Solving a Compound Inequality

Solve the compound inequality: \(3≤2x+2<6\)

The first method is to write two separate inequalities: \(3≤2x+2\) and \(2x+2<6.\) We solve them independently.

\[\begin{array}{lcr} 3≤2x+2 & \text{and} & 2x+2<6 \\[5pt] 1≤2x & & 2x<4 \\[5pt] \tfrac{1}{2}\leq x & & x < 2 \end{array} \nonumber\]

Then, we can rewrite the solution as a compound inequality, the same way the problem began.

\[\frac{1}{2}≤x<2\nonumber\]

In interval notation, the solution is written as \([\tfrac{1}{2},\, 2).\)

The second method is to leave the compound inequality intact, and perform solving procedures on the three parts at the same time.

\(\begin{align*} \qquad 3&≤2x+2<6 \\[5pt] 1&≤2x<4 & & \text{Isolate the variable term, and subtract }2\text{ from all three parts.} \\[5pt] \tfrac{1}{2}&≤x<2 & & \text{Divide through all three parts by }2. \end{align*}\)

We get the same solution: \([\tfrac{1}{2},\, 2).\)

Try It! \(\PageIndex{7}\)

Solve the compound inequality: \(4<2x−8≤10.\)

\(6<x≤9\) or \((6,9]\)

Example \(\PageIndex{8}\): Solving a Compound Inequality with the Variable in All Three Parts

Solve the compound inequality with variables in all three parts: \(3+x>7x−2>5x−10.\)

Let's try the first method. Write two inequalities:

\[\begin{array}{ccc} 3+x>7x−2 & \text{and} & 7x−2>5x−10\\[5pt] 3>6x−2 & & 2x−2>−10\\[5pt] 5>6x & & 2x>−8 \\[5pt] \tfrac{5}{6}>x & & -4<x \\[5pt] \end{array} \nonumber\]

The solution set is \(−4<𝑥<\tfrac{5}{6}\) or in interval notation \(\left(−4,\tfrac{5}{6}\right).\) Notice that when we write the solution in interval notation, the smaller number comes first. We read intervals from left to right, as they appear on a number line. See Figure \(\PageIndex{3}\).

Try It! \(\PageIndex{8}\)

Solve the compound inequality: \(3y<4−5y<5+3y.\)

\(\left(−\tfrac{1}{8},\, \tfrac{1}{2}\right)\)

Solving Absolute Value Inequalities

As we know, the absolute value of a quantity is a positive number or zero. From the origin, a point located at \((−x,\, 0)\) has an absolute value of \(x,\) as it is \(x\) units away. Consider absolute value as the distance from one point to another point. Regardless of direction, positive or negative, the distance between the two points is represented as a positive number or zero.

An absolute value inequality is an equation of the form

\[|A|<B,\quad |A|≤B, \quad |A|>B,\quad \text{or} \quad|A|≥B,\nonumber\]

Where \(A,\) and sometimes \(B,\) represents an algebraic expression dependent on a variable \(x.\) Solving the inequality means finding the set of all \(x\) - values that satisfy the problem. Usually this set will be an interval or the union of two intervals and will include a range of values.

There are two basic approaches to solving absolute value inequalities: graphical and algebraic. The advantage of the graphical approach is we can read the solution by interpreting the graphs of two equations. The advantage of the algebraic approach is that solutions are exact, as precise solutions are sometimes difficult to read from a graph.

Suppose we want to know all possible returns on an investment if we could earn some amount of money within $200 of $600. We can solve algebraically for the set of \(x\) - values such that the distance between\(x\) and \(600\) is less than or equal to \(200.\) We represent the distance between \(x\) and \(600\) as \(| x−600 |,\) and therefore, \(| x−600 |≤200\) or

\[\begin{array}{c} −200≤x−600≤200 \\ −200+600≤x−600+600≤200+600 \\ 400≤x≤800 \end{array} \nonumber\]

This means our returns would be between $400 and $800.

To solve absolute value inequalities, just as with absolute value equations, we write two inequalities and then solve them independently.

Definition: Absolute Value Inequalities

For an algebraic expression \(X\) and \(k>0,\) an absolute value inequality is an inequality of the form

\[\begin{align*} | X |&<k \text{ is equivalent to }−k<X<k\\[4pt] | X |&>k \text{ is equivalent to }X<−k \text{ or }X>k\end{align*}\]

These statements also apply to \(| X |≤k\) and \(| X |≥k.\)

Example \(\PageIndex{9}\): Determining a Number within a Prescribed Distance

Describe all values \(x\) within a distance of \(4\) from the number \(5.\)

We want the distance between \(x\) and \(5\) to be less than or equal to \(4.\) We can draw a number line, such as in Figure \(\PageIndex{4},\) to represent the condition to be satisfied.

The distance from \(x\) to \(5\) can be represented using an absolute value symbol, \(| x−5 |.\) Write the values of \(x\) that satisfy the condition as an absolute value inequality.

\[| x−5 |≤4\nonumber\]

We need to write two inequalities as there are always two solutions to an absolute value equation.

\[\begin{array}{ccc} x−5≤4 & \text{and} & x−5≥−4 \\[4pt] x≤9 & & x≥1 \end{array} \nonumber\]

If the solution set is \(x≤9\) and \(x≥1,\) then the solution set is an interval including all real numbers between and including 1 and 9.

So \(| x−5 |≤4\) is equivalent to \([ 1,9 ]\) in interval notation.

Try It! \(\PageIndex{9}\)

Describe all \(x\)-values within a distance of \(3\) from the number \(2.\)

\(|x−2|≤3\)

Example \(\PageIndex{10}\): Solving an Absolute Value Inequality

Solve \(|x−1|≤3.\)

\(\quad \begin{array}{c} |x−1 |≤3 \\[4pt] −3≤x−1≤3 \\[4pt] −2≤x≤4 \\[4pt] [−2,4] \end{array} \)

Example \(\PageIndex{11}\): Using a Graphical Approach to Solve Absolute Value Inequalities

Given the equation \(y=−\tfrac{1}{2}|4x−5|+3,\) determine the \(x\)-values for which the \(y\)-values are negative.

We are trying to determine where \(y<0,\) which is when \(−\tfrac{1}{2}|4x−5|+3<0.\) We begin by isolating the absolute value.

\[\begin{align*} −\tfrac{1}{2}|4x−5|&<−3 & & \text{Multiply both sides by }–2,\text{ and reverse the inequality.}\\[5pt] |4x−5|&>6 \end{align*} \]

Next, we solve for the equality \(|4x−5|=6.\)

\[\begin{array}{rcr} 4x−5=6 & & 4x−5=−6\\[5pt] 4x=11 & \text{or} & 4x=−1\\[5pt] x=\tfrac{11}{4} & & x=−\tfrac{1}{4} \end{array} \nonumber\]

Now, we can examine the graph to observe where the \(y\)-values are negative. We observe where the branches are below the \(x\)-axis. Notice that it is not important exactly what the graph looks like, as long as we know that it crosses the horizontal axis at \(x=−\tfrac{1}{4}\) and \(x=\tfrac{11}{4},\) and that the graph opens downward. See Figure \(\PageIndex{5}.\)

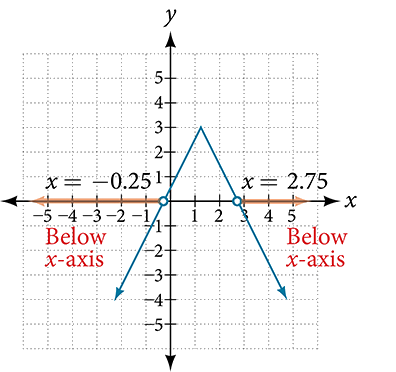
Try It! \(\PageIndex{10}\)

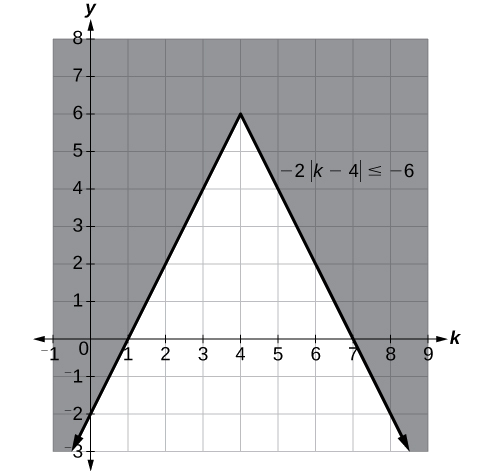
Solve \(−2|k−4|≤−6.\)

\(k≤1\) or \(k≥7;\) in interval notation, this would be \((−∞,1]∪[7,∞).\)

Teaching Absolute Value Equations and Inequalities

Absolute Value Equations and Inequalities are most easily related to Distance. We have an Algebra 2 Lesson that does a good job of explaining this. It can be found here: Absolute Value Functions and Graphs – Real World Applications

How Tough Are Absolute Value Equations and Inequalities?

When it comes to Algebra 1 this is probably one of the toughest lessons for the students all year. They have to have mastered how to solve both Absolute Value Equations and Inequalities separately. Then they have to put both of those skill sets together and remember all the rules that go with them. There are a lot for both.

• When to flip the inequality sign.
• When to split the two equations for Absolute Value.
• How to isolate the absolute value portion of the problem.
• How to graph each.

It is a lot for them to handle at once…

Use Multiple Days!

I always cover this lesson over multiple days and then sprinkle them in throughout the rest of the year.

Though, it is a very niche lesson meaning it doesn’t get used as much as some other topics. It is heavily covered in Algebra 2. They have to be prepared for that.

Here is your free content for this lesson!

Absolute Value Equations and Inequalities – PDFs

3-7 Worksheet  (Free) 3-7 Worksheet Answer Key ( Members Only ) 3-7 Bell Work  (Free) 3-7 Exit Quiz (Free) 3-7 Guide Notes SE  (Free) 3-7 Guided Notes Teacher Edition ( Members Only ) 3-7 Lesson Plan ( Members Only ) 3-7 Online Activities ( Members Only ) 3-7 Video Lesson ( Members Only ) 3-7 Slide Show  (Free) 3-7 Project ( Members Only )

Absolute Value Equations and Inequalities Worksheet Doc & PowerPoint

To gain access to our editable content Join the Algebra 1 Teacher Community! Here you will find hundreds of lessons, a community of teachers for support, and materials that are always up to date with the latest standards. Includes all… Worksheet 3-7 Worksheet 1-6 Solving Inequalities Worksheet  

Want access to everything?

Click Here to Get All of Our Lessons!

Solving Absolute Value Equations and Inequalities Worksheet Answer Key Algebra 1

Equations and Inequalities pdf

Looking for more Great Lessons?

Solving inequalities using addition and subtraction, teaching direct variation, teaching slope-intercept form, using graphs to relate two quantities, graphing a function rule, inequalities and their graphs, solving two-step equations, teaching operations on integers, multiplying binomials, teaching the real number system, if you love these materials don't forget to pin it.

Share this:

• Click to share on Facebook (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to share on Reddit (Opens in new window)
• Click to share on Twitter (Opens in new window)
• Click to print (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on Pocket (Opens in new window)
• Click to share on Tumblr (Opens in new window)

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing
• Alphabet Coloring
• Animals Coloring
• Birthday Coloring
• Boys Coloring
• Buildings Coloring
• Cartoons Coloring
• Christmas Coloring
• Country Flag Coloring
• Country Map Coloring
• Disney Coloring
• Fantasy Coloring
• Food Coloring
• Girls Coloring
• Holidays Coloring
• Music Coloring
• Nature Coloring
• New Year Coloring
• People Coloring
• Religious Coloring
• Sports Coloring
• Toys Coloring
• Transportation Coloring
• US Sports Team Coloring
• Valentine Day Coloring

Unit 1 Homework 6 Absolute Value Inequalities

Displaying top 8 worksheets found for - Unit 1 Homework 6 Absolute Value Inequalities .

Some of the worksheets for this concept are Solving absolute value equations and inequalities, Unit 1 equations and inequalities answers, Inequalities, Algebra 3 4 unit 1 absolute value functions and equations, Absolute value, Two step inequality word problems work answer key, Algebra 1 spencer unit 4 notes inequalities and, Notes unit 3 lesson 1 integers and absolute value.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Solving Absolute Value Equations and Inequalities

2. unit 1 equations and inequalities answers, 3. inequalities, 4. algebra 3-4 unit 1 absolute value functions and equations, 5. absolute value, 6. two step inequality word problems worksheet answer key, 7. algebra 1 spencer unit 4 notes: inequalities and ..., 8. notes: 3.1 (unit 3, lesson 1) integers and absolute value.