assignment problem vs travelling salesman problem

Traveling salesman problem

This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Traveling_salesman_problems

Author: Jessica Yu (ChE 345 Spring 2014)

Steward: Dajun Yue, Fengqi You

The traveling salesman problem (TSP) is a widely studied combinatorial optimization problem, which, given a set of cities and a cost to travel from one city to another, seeks to identify the tour that will allow a salesman to visit each city only once, starting and ending in the same city, at the minimum cost. 1

• 2.1 Graph Theory
• 2.2 Classifications of the TSP
• 2.3 Variations of the TSP
• 3.1 aTSP ILP Formulation
• 3.2 sTSP ILP Formulation
• 4.1 Exact algorithms
• 4.2.1 Tour construction procedures
• 4.2.2 Tour improvement procedures
• 5 Applications
• 7 References

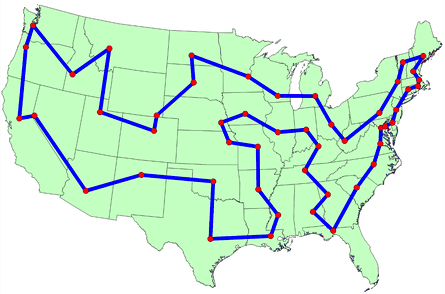
The origins of the traveling salesman problem are obscure; it is mentioned in an 1832 manual for traveling salesman, which included example tours of 45 German cities but gave no mathematical consideration. 2 W. R. Hamilton and Thomas Kirkman devised mathematical formulations of the problem in the 1800s. 2

It is believed that the general form was first studied by Karl Menger in Vienna and Harvard in the 1930s. 2,3

Hassler Whitney, who was working on his Ph.D. research at Harvard when Menger was a visiting lecturer, is believed to have posed the problem of finding the shortest route between the 48 states of the United States during either his 1931-1932 or 1934 seminar talks. 2 There is also uncertainty surrounding the individual who coined the name “traveling salesman problem” for Whitney’s problem. 2

The problem became increasingly popular in the 1950s and 1960s. Notably, George Dantzig, Delber R. Fulkerson, and Selmer M. Johnson at the RAND Corporation in Santa Monica, California solved the 48 state problem by formulating it as a linear programming problem. 2 The methods described in the paper set the foundation for future work in combinatorial optimization, especially highlighting the importance of cutting planes. 2,4

In the early 1970s, the concept of P vs. NP problems created buzz in the theoretical computer science community. In 1972, Richard Karp demonstrated that the Hamiltonian cycle problem was NP-complete, implying that the traveling salesman problem was NP-hard. 4

Increasingly sophisticated codes led to rapid increases in the sizes of the traveling salesman problems solved. Dantzig, Fulkerson, and Johnson had solved a 48 city instance of the problem in 1954. 5 Martin Grötechel more than doubled this 23 years later, solving a 120 city instance in 1977. 5 Enoch Crowder and Manfred W. Padberg again more than doubled this in just 3 years, with a 318 city solution. 5

In 1987, rapid improvements were made, culminating in a 2,392 city solution by Padberg and Giovanni Rinaldi. In the following two decades, David L. Appelgate, Robert E. Bixby, Vasek Chvátal, & William J. Cook led the cutting edge, solving a 7,397 city instance in 1994 up to the current largest solved problem of 24,978 cities in 2004. 5

Description

Graph theory.

Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G = (V, E)} be a directed or undirected graph with set of vertices Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} and set of edges Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = \{(x,y) | x, y \in V\}} . 3,6 Each edge Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e \in E} is assigned a cost Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_e} . Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{H}} be the set of all Hamiltonian cycles, a cycle that visits each vertex exactly once, in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} . 6 The traveling salesman problem is to find the tour Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h \in \mathbb{H}} such that the sum of the costs Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_e} in the tour is minimized.

Suppose graph Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} is a complete graph, where every pair of distinct vertices is connected by a unique edge. 6 Let the set of vertices be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = \{v_1, v_2, ..., v_n\}} . The cost matrix is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C = (c_{ij})_{n \times n}} where the cost of the edge joining node Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_i} to node Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_j} , denoted Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{ij}} , is given in entry Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (i,j)} .

In the context of the traveling salesman problem, the verticies correspond to cities and the edges correspond to the path between those cities. When modeled as a complete graph, paths that do not exist between cities can be modeled as edges of very large cost without loss of generality. 6 Minimizing the sum of the costs for Hamiltonian cycle is equivalent to identifying the shortest path in which each city is visiting only once.

Classifications of the TSP

The TRP can be divided into two classes depending on the nature of the cost matrix. 3,6

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} is undirected
• Applies when the distance between cities is the same in both directions
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} is directed
• Applies when there are differences in distances (e.g. one-way streets)

An ATSP can be formulated as an STSP by doubling the number of nodes. 6

Variations of the TSP

Formulation.

Given a set of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} cities enumerated Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0, 1, ..., n-1} to be visited with the distance between each pair of cities Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{ij}} . 1 Introduce decision variables Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{ij}} for each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (i,j)} such that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{ij} = \begin{cases} 1 ~~\text{if city }j\text{ is visited immediately after city }i\\ 0 ~~\text{otherwise} \end{cases} }

The objective function is then given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{min} \sum_i \sum_j c_{ij}y_{ij} }

To ensure that the result is a valid tour, several contraints must be added. 1,3

There are several other formulations for the subtour elimnation contraint, including circuit packing contraints, MTZ constraints, and network flow constraints.

aTSP ILP Formulation

The integer linear programming formulation for an aTSP is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \text{min} & ~~ \sum_i \sum_j c_{ij}y_{ij}\\ \text{s.t} & ~~ \sum_j y_{ij} = 1, ~~ i = 0, 1, ..., n-1 \\ & ~~ \sum_i y_{ij} = 1, ~~ j = 0, 1, ..., n-1 \\ & ~~ \sum_i \sum_j y_{ij} \le |S| - 1 ~~ S \subset V, 2 \le |S| \le n - 2 \\ & ~~ y_{ij} \in \{0,1\}, ~ \forall i,j \in E \\ \end{align} }

sTSP ILP Formulation

The symmetric case is a special case of the asymmetric case and the above formulation is valid. 3, 6 The integer linear programming formulation for an sTSP is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \text{min} & ~~ \sum_i \sum_j c_{ij}y_{ij}\\ \text{s.t} & ~~ \sum_{i < k} y_{ik} + \sum_{j > k} y_{kj} = 2, ~~ k \in V \\ & ~~ \sum_i \sum_j y_{ij} \le |S| - 1 ~~ S \subset V, 3 \le |S| \le n - 3 \\ & ~~ y_{ij} \in \{0,1\} ~ \forall i,j \in E \\ \end{align} }

Exact algorithms

The most direct solution algorithm is a complete enumeration of all possible path to determine the path of least cost. However, for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} cities, the problem is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O(n!)} time, and this method is practical only for extremely small values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .

Branch-and-bound algorithms are commonly used to find solutions for TSPs. 7 The ILP is first relaxed and solved as an LP using the Simplex method, then feasibility is regained by enumeration of the integer variables. 7

Other exact solution methods include the cutting plane method and branch-and-cut. 8

Heuristic algorithms

Given that the TSP is an NP-hard problem, heuristic algorithms are commonly used to give a approximate solutions that are good, though not necessarily optimal. The algorithms do not guarantee an optimal solution, but gives near-optimal solutions in reasonable computational time. 3 The Held-Karp lower bound can be calculated and used to judge the performance of a heuristic algorithm. 3

There are two general heuristic classifications 7 :

• Tour construction procedures where a solution is gradually built by adding a new vertex at each step
• Tour improvement procedures where a feasbile solution is improved upon by performing various exchanges

The best methods tend to be composite algorithms that combine these features. 7

Tour construction procedures

Tour improvement procedures, applications.

The importance of the traveling salesman problem is two fold. First its ubiquity as a platform for the study of general methods than can then be applied to a variety of other discrete optimization problems. 5 Second is its diverse range of applications, in fields including mathematics, computer science, genetics, and engineering. 5,6

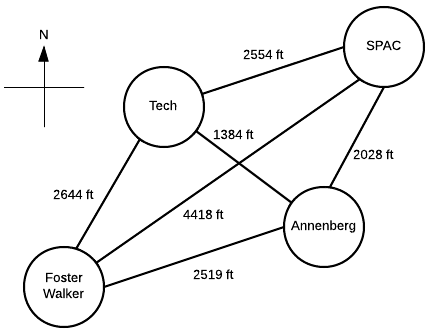
Suppose a Northwestern student, who lives in Foster-Walker , has to accomplish the following tasks:

• Drop off a homework set at Tech
• Work out a SPAC
• Complete a group project at Annenberg

Distances between buildings can be found using Google Maps. Note that there is particularly strong western wind and walking east takes 1.5 times as long.

It is the middle of winter and the student wants to spend the least possible time walking. Determine the path the student should take in order to minimize walking time, starting and ending at Foster-Walker.

Start with the cost matrix (with altered distances taken into account):

Method 1: Complete Enumeration

All possible paths are considered and the path of least cost is the optimal solution. Note that this method is only feasible given the small size of the problem.

From inspection, we see that Path 4 is the shortest. So, the student should walk 2.28 miles in the following order: Foster-Walker → Annenberg → SPAC → Tech → Foster-Walker

Method 2: Nearest neighbor

Starting from Foster-Walker, the next building is simply the closest building that has not yet been visited. With only four nodes, this can be done by inspection:

• Smallest distance is from Foster-Walker is to Annenberg
• Smallest distance from Annenberg is to Tech
• Smallest distance from Tech is to Annenberg ( creates a subtour, therefore skip )
• Next smallest distance from Tech is to Foster-Walker ( creates a subtour, therefore skip )
• Next smallest distance from Tech is to SPAC
• Smallest distance from SPAC is to Annenberg ( creates a subtour, therefore skip )
• Next smallest distance from SPAC is to Tech ( creates a subtour, therefore skip )
• Next smallest distance from SPAC is to Foster-Walker

So, the student would walk 2.54 miles in the following order: Foster-Walker → Annenberg → Tech → SPAC → Foster-Walker

Method 3: Greedy

With this method, the shortest paths that do not create a subtour are selected until a complete tour is created.

• Smallest distance is Annenberg → Tech
• Next smallest is SPAC → Annenberg
• Next smallest is Tech → Annenberg ( creates a subtour, therefore skip )
• Next smallest is Anneberg → Foster-Walker ( creates a subtour, therefore skip )
• Next smallest is SPAC → Tech ( creates a subtour, therefore skip )
• Next smallest is Tech → Foster-Walker
• Next smallest is Annenberg → SPAC ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → Annenberg ( creates a subtour, therefore skip )
• Next smallest is Tech → SPAC ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → Tech ( creates a subtour, therefore skip )
• Next smallest is SPAC → Foster-Walker ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → SPAC

So, the student would walk 2.40 miles in the following order: Foster-Walker → SPAC → Annenberg → Tech → Foster-Walker

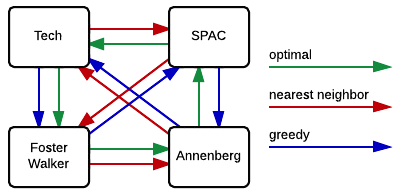
As we can see in the figure to the right, the heuristic methods did not give the optimal solution. That is not to say that heuristics can never give the optimal solution, just that it is not guaranteed.

Both the optimal and the nearest neighbor algorithms suggest that Annenberg is the optimal first building to visit. However, the optimal solution then goes to SPAC, while both heuristic methods suggest Tech. This is in part due to the large cost of SPAC → Foster-Walker. The heuristic algorithms cannot take this future cost into account, and therefore fall into that local optimum.

We note that the nearest neighbor and greedy algorithms give solutions that are 11.4% and 5.3%, respectively, above the optimal solution. In the scale of this problem, this corresponds to fractions of a mile. We also note that neither heuristic gave the worst case result, Foster-Walker → SPAC → Tech → Annenberg → Foster-Walker.

Only tour building heuristics were used. Combined with a tour improvement algorithm (such as 2-opt or simulated annealing), we imagine that we may be able to locate solutions that are closer to the optimum.

The exact algorithm used was complete enumeration, but we note that this is impractical even for 7 nodes (6! or 720 different possibilities). Commonly, the problem would be formulated and solved as an ILP to obtain exact solutions.

• Vanderbei, R. J. (2001). Linear programming: Foundations and extensions (2nd ed.). Boston: Kluwer Academic.
• Schrijver, A. (n.d.). On the history of combinatorial optimization (till 1960).
• Matai, R., Singh, S., & Lal, M. (2010). Traveling salesman problem: An overview of applications, formulations, and solution approaches. In D. Davendra (Ed.), Traveling Salesman Problem, Theory and Applications . InTech.
• Junger, M., Liebling, T., Naddef, D., Nemhauser, G., Pulleyblank, W., Reinelt, G., Rinaldi, G., & Wolsey, L. (Eds.). (2009). 50 years of integer programming, 1958-2008: The early years and state-of-the-art surveys . Heidelberg: Springer.
• Cook, W. (2007). History of the TSP. The Traveling Salesman Problem . Retrieved from http://www.math.uwaterloo.ca/tsp/history/index.htm
• Punnen, A. P. (2002). The traveling salesman problem: Applications, formulations and variations. In G. Gutin & A. P. Punnen (Eds.), The Traveling Salesman Problem and its Variations . Netherlands: Kluwer Academic Publishers.
• Laporte, G. (1992). The traveling salesman problem: An overview of exact and approximate algorithms. European Journal of Operational Research, 59 (2), 231–247.
• Goyal, S. (n.d.). A suvey on travlling salesman problem.
• Pages with math errors
• Pages with math render errors

Navigation menu

Reset password New user? Sign up

Existing user? Log in

Traveling Salesperson Problem

Already have an account? Log in here.

A salesperson needs to visit a set of cities to sell their goods. They know how many cities they need to go to and the distances between each city. In what order should the salesperson visit each city exactly once so that they minimize their travel time and so that they end their journey in their city of origin?

The traveling salesperson problem is an extremely old problem in computer science that is an extension of the Hamiltonian Circuit Problem . It has important implications in complexity theory and the P versus NP problem because it is an NP-Complete problem . This means that a solution to this problem cannot be found in polynomial time (it takes superpolynomial time to compute an answer). In other words, as the number of vertices increases linearly, the computation time to solve the problem increases exponentially.

The following image is a simple example of a network of cities connected by edges of a specific distance. The origin city is also marked.

Network of cities

Here is the solution for that network, it has a distance traveled of only 14. Any other path that the salesman can takes will result in a path length that is more than 14.

Relationship to Graphs

Special kinds of tsp, importance for p vs np, applications.

The traveling salesperson problem can be modeled as a graph . Specifically, it is typical a directed, weighted graph. Each city acts as a vertex and each path between cities is an edge. Instead of distances, each edge has a weight associated with it. In this model, the goal of the traveling salesperson problem can be defined as finding a path that visits every vertex, returns to the original vertex, and minimizes total weight.

To that end, many graph algorithms can be used on this model. Search algorithms like breadth-first search (BFS) , depth-first search (DFS) , and Dijkstra's shortest path algorithm can certainly be used, however, they do not take into consideration that fact that every vertex must be visited.

The Traveling Salesperson Problem (TSP), an NP-Complete problem, is notoriously complicated to solve. That is because the greedy approach is so computational intensive. The greedy approach to solving this problem would be to try every single possible path and see which one is the fastest. Try this conceptual question to see if you have a grasp for how hard it is to solve.

For a fully connected map with \(n\) cities, how many total paths are possible for the traveling salesperson? Show Answer There are (n-1)! total paths the salesperson can take. The computation needed to solve this problem in this way grows far too quickly to be a reasonable solution. If this map has only 5 cities, there are \(4!\), or 24, paths. However, if the size of this map is increased to 20 cities, there will be \(1.22 \cdot 10^{17}\) paths!

The greedy approach to TSP would go like this:

• Find all possible paths.
• Find the cost of every paths.
• Choose the path with the lowest cost.

Another version of a greedy approach might be: At every step in the algorithm, choose the best possible path. This version might go a little quicker, but it's not guaranteed to find the best answer, or an answer at all since it might hit a dead end.

For NP-Hard problems (a subset of NP-Complete problems) like TSP, exact solutions can only be implemented in a reasonable amount of time for small input sizes (maps with few cities). Otherwise, the best approach we can do is provide a heuristic to help the problem move forward in an optimal way. However, these approaches cannot be proven to be optimal because they always have some sort of downside.

Small input sizes

As described, in a previous section , the greedy approach to this problem has a complexity of \(O(n!)\). However, there are some approaches that decrease this computation time.

The Held-Karp Algorithm is one of the earliest applications of dynamic programming . Its complexity is much lower than the greedy approach at \(O(n^2 2^n)\). Basically what this algorithm says is that every sub path along an optimal path is itself an optimal path. So, computing an optimal path is the same as computing many smaller subpaths and adding them together.

Heuristics are a way of ranking possible next steps in an algorithm in the hopes of cutting down computation time for the entire algorithm. They are often a tradeoff of some attribute - such as completeness, accuracy, or precision - in favor of speed. Heuristics exist for the traveling salesperson problem as well.

The most simple heuristic for this problem is the greedy heuristic. This heuristic simply says, at each step of the network traversal, choose the best next step. In other words, always choose the closest city that you have not yet visited. This heuristic seems like a good one because it is simple and intuitive, and it is even used in practice sometimes, however there are heuristics that are proven to be more effective.

Christofides algorithm is another heuristic. It produces at most 1.5 times the optimal weight for TSP. This algorithm involves finding a minimum spanning tree for the network. Next, it creates matchings for the cities of an odd degree (meaning they have an odd number of edges coming out of them), calculates an eulerian path , and converts back to a TSP path.

Even though it is typically impossible to optimally solve TSP problems, there are cases of TSP problems that can be solved if certain conditions hold.

The metric-TSP is an instance of TSP that satisfies this condition: The distance from city A to city B is less than or equal to the distance from city A to city C plus the distance from city C to city B. Or,

\[distance_{AB} \leq distance_{AC} + distance_{CB}\]

This is a condition that holds in the real world, but it can't always be expected to hold for every TSP problem. But, with this inequality in place, the approximated path will be no more than twice the optimal path. Even better, we can bound the solution to a \(3/2\) approximation by using Christofide's Algorithm .

The euclidean-TSP has an even stricter constraint on the TSP input. It states that all cities' edges in the network must obey euclidean distances . Recent advances have shown that approximation algorithms using euclidean minimum spanning trees have reduced the runtime of euclidean-TSP, even though they are also NP-hard. In practice, though, simpler heuristics are still used.

The P versus NP problem is one of the leading questions in modern computer science. It asks whether or not every problem whose solution can be verified in polynomial time by a computer can also be solved in polynomial time by a computer. TSP, for example, cannot be solved in polynomial time (at least that's what is currently theorized). However, TSP can be solved in polynomial time when it is phrased like this: Given a graph and an integer, x, decide if there is a path of length x or less than x . It's easy to see that given a proposed answer to this question, it is simple to check if it is less than or equal to x.

The traveling salesperson problem, like other problems that are NP-Complete, are very important to this debate. That is because if a polynomial time solution can be found to this problems, then \(P = NP\). As it stands, most scientists believe that \(P \ne NP\).

The traveling salesperson problem has many applications. The obvious ones are in the transportation space. Planning delivery routes or flight patterns, for example, would benefit immensly from breakthroughs is this problem or in the P versus NP problem .

However, this same logic can be applied to many facets of planning as well. In robotics, for instance, planning the order in which to drill holes in a circuit board is a complex task due to the sheer number of holes that must be drawn.

The best and most important application of TSP, however, comes from the fact that it is an NP-Complete problem. That means that its practical applications amount to the applications of any problem that is NP-Complete. So, if there are significant breakthroughs for TSP, that means that those exact same breakthrough can be applied to any problem in the NP-Complete class.

Problem Loading...

Note Loading...

Set Loading...

Learning center series

Travelling salesman problem explained

• Published on April 26, 2024
• by Oguzhan Uyar
• Last updated: 6 days ago

Revolutionize your understanding of the Travelling Salesman Problem (TSP); a mind-boggling conundrum that has compelled academia and industry alike. In the upcoming lines, we decode the key concepts, algorithms, and anticipated solutions for 2024 to this age-old dilemma.

Now, picture the TSP as a globetrotting traveling salesman who’s whirlwind journey. He must stop at every city once, only the origin city once, and find the quickest shortest possible route back home. If daunting to visualize, consider this: the possible number of routes in the problem concerning just 20 cities exceeds the number of atoms in the observable universe.

Fathom the sheer magnitude?

So, what is the Travelling Salesman Problem, and why has it remained unsolved for years? Let’s snap together the puzzle of this notorious problem that spans mathematics, computer science, and beyond. Welcome to an insightful voyage into the astonishing world of the TSP.

Understanding the Travelling Salesman Problem (TSP): Key Concepts and Algorithms

Defining the travelling salesman problem: a comprehensive overview.

The Travelling Salesman Problem, often abbreviated as TSP, has a strong footing in the realm of computer science. To the untrained eye, it presents itself as a puzzle: a salesperson or traveling salesman must traverse through a number of specific cities before an ending point and return to their ending point as of origin, managing to do so in the shortest possible distance. But this problem is not simply a conundrum for those fond of riddles; it holds immense significance in the broad field of computer science and optimization. Optimizing travel routes is the key to solving the Travelling Salesman Problem efficiently, ensuring the shortest and most cost-effective journey for salespeople or travelers.

The sheer computational complexity of TSP is what sets it apart, and incidentally, why it is considered a challenging problem to solve. Its complexity derives from the factorial nature of the problem: whenever a new city is added, the total number of possibilities increases exponentially. Thus, as the problem scope enlarges, it swiftly becomes computationally prohibitive to simply calculate all possible solutions to identify an optimal shortest route through. Consequently, developing effective and efficient algorithms to solve the TSP has become a priority in the world of computational complexity.

Polynomial Time Solution: The TSP can be solved by a deterministic Turing machine in polynomial time, which means that the number of steps to solve the problem can be at most 1.5 times the optimal global solution.

One such algorithm is the dynamic programming approach that can solve TSP problems in polynomial time. The approach uses a recursive formula to compute the shortest possible route that visits all other nodes in the cities exactly once and ends at all nodes in the starting point or city. Moreover, linear programming and approximation algorithms have also been used to find near-optimal solutions.

Unraveling TSP Algorithms: From Brute Force to Heuristics

A multitude of algorithms have been developed to contend with the TSP. The brute force method, for example, entails considering the shortest distance for all possible permutations of cities, calculating the total distance for six cities along each route, and selecting the shortest distance for one. While brute force promises an optimal solution, it suffers from exponential computational complexity, rendering it unfeasible for large datasets.

TSP Complexity: A TSP with just 10 cities has 362,880 possible routes , making brute force infeasible for larger instances.

On the other hand, we have heuristic algorithms that generate good, albeit non-optimal, solutions in reasonable timeframes. The greedy algorithm, for instance, initiates from a starting city and looks for the shortest distance from other nodes to the next node minimizes the distance, and guarantees speed but is not necessarily an optimal solution.

Algorithmic Potential: Local Solutions 4/3 Times Optimal Global: The theoretical conjecture suggests an algorithm that can provide a local solution within 4/3 times the optimal global solution.

Record Local TSP Solution: The record for a local solution to the Traveling Salesman Problem (TSP) is 1.4 times the optimal global solution, achieved in September 2012 by Andr´as Seb˝o and Jens Vygen.

Exploring further, we encounter more refined heuristic solutions such as the genetic algorithm and simulated annealing algorithm. These algorithms deploy probabilistic rules, with the former incorporating principles of natural evolution and the latter being inspired by the cooling process in metallurgy. They differ significantly from each other in terms of how they search for solutions, but when compared to brute force, they often offer a promising trade-off between quality and computational effort.

Certainly, the TSP is far more than a problem to puzzle over during a Sunday afternoon tea. It’s a complex computational task with real-world implications, and unraveling it requires more than brute force; it demands the application of sophisticated algorithms designed to balance efficiency and quality of results. Nevertheless, with a better understanding of the problem statement and its dynamics, you can unlock the potential to not just solve problems faster, but to do so more intelligently.

Practical Solutions to the Travelling Salesman Problem

Implementing tsp solutions: a step-by-step guide, a comprehensive process for implementing tsp solutions.

Developing complete, practical solutions for the Travelling Salesman Problem (TSP) requires a good grasp of specific algorithms. Visual aids, for example, such as finding all the edges leading out of a given city, can help to simplify the process. Enhance your ability to solve the Travelling Salesman Problem by mastering route optimization with Google Maps , streamlining your path and saving significant time on the go.

TSP's Computer Science Quest for Shortest Routes: The TSP involves finding the shortest route to visit a set of cities exactly once before returning to the starting city, aiming to minimize travel distance.

One popular approach to TSP problem solving is the dynamic programming approach, which involves breaking down the problem into smaller sub-problems and recursively solving them. Other approaches include approximation algorithms, which generate near-optimal solutions to small problems in polynomial time, and bound algorithms, which aim to find an upper bound on the optimal solution given graph top.

TSP Variants: ASTP and STSP The TSP can be divided into two types: the asymmetric traveling salesman problem (ASTP) and the symmetric traveling salesman problem (STSP)

Practical code implementation

Before diving into code manipulations, it’s worth noting that practical implementation varies based on the specifics of the problem and the chosen algorithm. Let’s further deconstruct these notions by examining the steps for code implementation for a pre-determined shortest path first. It’s crucial to efficiently concede each point of the shortest path, call other nodes, connect each node, and conclude each route. Hereby, I shall delve into the practicalities of coding from an output standpoint, concentrating on readability, scalability, and execution efficiency.

TSP Instance Size: The size of the TSP instances used in the studies is 100 nodes.

Cluster Quantity in TSP Instances: The number of clusters in the TSP instances used in the studies is 10 .

The Quantity of Instances per Cluster in Studies: The number of instances in each cluster used in the studies is 100.

Optimizing TSP Solutions: Tips and Tricks

Tsp solutions optimization techniques.

An optimized solution for the TSP is often accomplished using advanced algorithms and techniques. Optimization techniques allow professionals to solve more intricate problems, rendering them invaluable tools when handling large datasets and attempting to achieve the best possible solution. Several approaches can be taken, such as heuristic and metaheuristic approaches, that can provide near-optimal solutions with less use of resources.

Expert Advice for Maximum Efficiency Minimum Cost

Even the most proficient problem solvers can gain from learning expert tips and tricks. These nuggets of wisdom often provide the breakthrough needed to turn a good solution into a great one. The TSP is no exception. Peering into the realm of experts can provide novel and creative ways to save time, increase computation speed, manage datasets, and achieve the most efficient shortest route around.

By comprehending and implementing these solutions to the Travelling Salesman Problem, one can unravel the complex web of nodes and paths. This equips any problem-solver with invaluable insights that make navigating through real-world TSP applications much more manageable. By adopting sophisticated routing planner software , businesses can significantly streamline their delivery operations, ensuring a more predictable and cost-effective way of dealing with the challenges presented by the Travelling Salesman Problem.

Real-World Applications of the Travelling Salesman Problem

Tsp in logistics and supply chain management.

The Travelling Salesman Problem (TSP) is not confined to theoretical mathematics or theoretical computer science either, it shines in real-world applications too. One of its most potent applications resides in the field of logistics and supply chain management. Explore how the latest gratis route planning applications can revolutionize logistics and supply chain efficiency by uncovering the top 10 free software tools for 2024.

With globalization, the importance of more efficient routes for logistics and supply chain operations has risen dramatically. Optimizing routes and decreasing costs hold the key to success in this arena. Here’s where TSP comes into play. Discover how Planning for Multiple Stops can revolutionize your logistics, ensuring the most efficient paths are taken. Dive into our post to see how it streamlines operations and reduces expenses.

In the vast complexity of supply chain networks, routing can be a colossal task. TSP algorithms bring clarity to the chaos, eliminating redundant paths and pointing to the optimal route covering the most distance, shortest path, and least distance between all the necessary points—leading to a drastic dip in transportation costs and delivery times. Uncover how optimizing delivery routes can revolutionize your logistics, ensuring efficiency and cost-effectiveness in your delivery operations.

Real-World Examples

Consider the case of UPS – the multinational package delivery company. They’ve reportedly saved hundreds of millions of dollars yearly by implementing route optimization algorithms originating from the Travelling Salesman Problem. The solution, named ORION, helped UPS reduce the distance driven by their drivers roughly by 100 million miles annually.

TSP in GIS and Urban Planning: Optimal Route

TSP’s contributions to cities aren’t confined to logistics; it is invaluable in Geographic Information Systems (GIS) and urban planning as well. A city’s efficiency revolves around transportation. The better the transport networks and systems, the higher the city’s productivity. And as city authorities continuously strive to upgrade transportation systems, they find an ally in TSP. Discover how TSP enhances road architecture by integrating specialized truck routing solutions , elevating urban transport strategies.

Advanced GIS systems apply TSP to design more efficient routes and routing systems for public transportation. The aim of the route is to reach maximum locations with the least travel time and least distance, ensuring essential amenities are accessible to everyone in the city.

The city of Singapore, known for its efficient public transportation system, owes part of its success to similar routing algorithms. The Land Transport Authority uses TSP-related solutions to plan bus routes, reducing travel durations and enhancing accessibility across the city.

Delving Deeper: The Complexity and History of the Travelling Salesman Problem

Understanding the complexity of tsp.

TSP is fascinating not just for its inherent practicality but also for the complexity it brings along. TSP belongs to a class of problems known as NP-hard, a category that houses some of the most complex problems in computer science. But what makes TSP so gnarled?

Unravel the Intricacies: Why is TSP complex?

TSP is a combinatorial optimization problem, which simply means that it’s all about figuring out the most often optimal solution among a vast number of possible solutions or combinations of approximate solutions. The real challenge comes from an innocent-sounding feature of TSP: As the number of cities (we call them nodes) increases, the complexity heightens exponentially, not linearly. The number of possible routes takes a dramatic upward turn as you add more nodes, clearly exemplifying why TSP is no walk-in-the-park problem.

NP-hard and TSP: A Connection Explored

In computer science, we use the terms P and NP for classifying problems. P stands for problems where a solution can be found in ‘polynomial time’. NP stands for ‘nondeterministic polynomial time’, which includes problems where a solution can be verified in polynomial time. The concept of ‘NP-hardness’ applies to TSP. Any problem that can be ‘reduced’ to an NP problem in polynomial time is described as NP-hard. In simpler terms, it’s harder than the hardest problems of NP. TSP holds a famed position in this class, making it a noteworthy example of an NP-hard problem. Discovering efficient solutions for the Traveling Salesman Problem (TSP) exemplifies how optimizing routes can streamline complex logistical challenges, showcasing the practical impact of advancements in algorithmic route optimization.

A Look Back: The History of the Travelling Salesman Problem

TSP is not a new kid on the block. Its roots can be traced back to the 1800s, and the journey since then has been nothing short of a compelling tale of mathematical and computational advancements.

The Origins and Evolution of TSP

Believe it or not, the Travelling Salesman Problem was first formulated as a mathematical problem in the 1800s. This was way before the advent of modern computers. Mathematicians and logisticians were intrigued by the problem and its implications. However, it wasn’t until the mid-20th century that the problem started to gain more widespread attention. Over the years, the TSP has transformed from a theoretical model to a practical problem that helps solve real-world issues.

A Classic Shortest Route Problem Since 1930s: The TSP is a classic optimization problem within the field of operations research, first studied during the 1930s.

Milestones in TSP Research

Looking at all the cities and milestones in TSP research, the story is truly impressive. From some of the initial heuristic algorithms to solve smaller instances of TSP, to geometric methods and then approximation algorithms, TSP research has seen a lot. More recently, we have also seen practical solutions to TSP using quantum computing — a testament to how far we’ve come. Each of these milestones signifies an innovative shift in how we understand and solve TSP. Discovering the top delivery route planning software in 2024, we navigated through the advancements in TSP solutions to identify which applications excel in streamlining delivery logistics.

Wrapping Up The Journey With Algorithms and Solutions

The Travelling Salesman Problem (TSP) remains a complex enigma of business logistics, yet, the advent of sophisticated algorithms and innovative solutions are paving avenues to optimize routing, reduce travel costs further, and enhance customer interactions.

Navigating the TSP intricacies is no longer a daunting challenge but a worthwhile investment in refining operational efficiency and delivering unparalleled customer experiences. With advanced toolsets and intelligent systems, businesses are closer to making more informed, strategic decisions.

Now, it’s your turn. Reflect on your current logistics complexities. How can your business benefit from implementing these key concepts and algorithms? Consider where you could incorporate these practices to streamline and revolutionize your daily operations.

Remember, in the world of dynamic business operations, mastering the TSP is not just an option, but a strategic imperative. As you move forward into 2024, embrace the art of solving the TSP. Unravel the potential, decipher the complexities, and unlock new horizons for your business.

Ready for the challenge?

What is route optimization?

7 reasons for delivery route optimization

What is multi-stop route planning and why is it important?

How to optimize routes with Google Maps

7 benefits of using route scheduling software

Truck route planning vs common route planning

Best delivery route planning software for 2024

Top 10 free route planning software of 2024

‟Powerful Route Planning”

Rebel Bread

‟I am able to do twice as many orders because I don't spend time delivering”

‟3 Metrobi Drivers together completed more than 170 deliveries for us.”

Diamond Bakery

‟The most seamless & smoothest Valentine's Day”

Hanato Floral Design

Success Stories

Benz’s Food Products Inc.

Field Trip Flowers

Bartleby’s Ice Cream Cakes

DELIVER WITH METROBI

Grow with confidence

• 55 Court St floor 2, Boston, MA 02108
• [email protected]
• Team Metrobi
• Privacy policy
• Terms of service
• Write for us

Refer us to a company, you earn $250 and they earn $250. Learn more

• Shopify Delivery Planner App
• Delivery Management Software
• Atlanta courier service
• Boston courier service
• Chicago courier service
• Denver courier service
• Miami courier service
• New York City courier service
• Los Angeles courier service
• Philadelphia courier service
• San Francisco courier service
• Washington DC courier service
• See all locations
• Bulk Order Delivery Service
• Express Urgent Delivery Service
• Fixed Route Delivery Service
• On Demand Delivery Service
• Overnight Delivery Service
• Same Day Delivery Service
• Scheduled Delivery Service
• Wholesale Delivery Service
• See all delivery services
• Metrobi vs. Onfleet
• Metrobi vs. Roadie
• Metrobi vs. Roadie Support
• Artisan Food
• Food Producers

Want to access our large pool of drivers?

We started Metrobi to take operations off your plate. We provide drivers (rated 4.97/5), dedicated operation managers (70% cheaper), and routing software with a receiver notification system.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

12.10: Traveling Salesperson Problem

• Last updated
• Save as PDF
• Page ID 129677

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

After completing this section, you should be able to:

• Distinguish between brute force algorithms and greedy algorithms.
• List all distinct Hamilton cycles of a complete graph.
• Apply brute force method to solve traveling salesperson applications.
• Apply nearest neighbor method to solve traveling salesperson applications.

We looked at Hamilton cycles and paths in the previous sections Hamilton Cycles and Hamilton Paths. In this section, we will analyze Hamilton cycles in complete weighted graphs to find the shortest route to visit a number of locations and return to the starting point. Besides the many routing applications in which we need the shortest distance, there are also applications in which we search for the route that is least expensive or takes the least time. Here are a few less common applications that you can read about on a website set up by the mathematics department at the University of Waterloo in Ontario, Canada:

• Design of fiber optic networks
• Minimizing fuel expenses for repositioning satellites
• Development of semi-conductors for microchips
• A technique for mapping mammalian chromosomes in genome sequencing

Before we look at approaches to solving applications like these, let's discuss the two types of algorithms we will use.

Brute Force and Greedy Algorithms

An algorithm is a sequence of steps that can be used to solve a particular problem. We have solved many problems in this chapter, and the procedures that we used were different types of algorithms. In this section, we will use two common types of algorithms, a brute force algorithm and a greedy algorithm . A brute force algorithm begins by listing every possible solution and applying each one until the best solution is found. A greedy algorithm approaches a problem in stages, making the apparent best choice at each stage, then linking the choices together into an overall solution which may or may not be the best solution.

To understand the difference between these two algorithms, consider the tree diagram in Figure 12.214. Suppose we want to find the path from left to right with the largest total sum. For example, branch A in the tree diagram has a sum of 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36 .

To be certain that you pick the branch with greatest sum, you could list each sum from each of the different branches:

A : 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36

B : 10 + 2 + 11 + 8 = 31 10 + 2 + 11 + 8 = 31

C : 10 + 2 + 15 + 1 = 28 10 + 2 + 15 + 1 = 28

D : 10 + 2 + 15 + 6 = 33 10 + 2 + 15 + 6 = 33

E : 10 + 7 + 3 + 20 = 40 10 + 7 + 3 + 20 = 40

F : 10 + 7 + 3 + 14 = 34 10 + 7 + 3 + 14 = 34

G : 10 + 7 + 4 + 11 = 32 10 + 7 + 4 + 11 = 32

H : 10 + 7 + 4 + 5 = 26 10 + 7 + 4 + 5 = 26

Then we know with certainty that branch E has the greatest sum.

Now suppose that you wanted to find the branch with the highest value, but you only were shown the tree diagram in phases, one step at a time.

After phase 1, you would have chosen the branch with 10 and 7. So far, you are following the same branch. Let’s look at the next phase.

After phase 2, based on the information you have, you will choose the branch with 10, 7 and 4. Now, you are following a different branch than before, but it is the best choice based on the information you have. Let’s look at the last phase.

After phase 3, you will choose branch G which has a sum of 32.

The process of adding the values on each branch and selecting the highest sum is an example of a brute force algorithm because all options were explored in detail. The process of choosing the branch in phases, based on the best choice at each phase is a greedy algorithm. Although a brute force algorithm gives us the ideal solution, it can take a very long time to implement. Imagine a tree diagram with thousands or even millions of branches. It might not be possible to check all the sums. A greedy algorithm, on the other hand, can be completed in a relatively short time, and generally leads to good solutions, but not necessarily the ideal solution.

Example 12.42

Distinguishing between brute force and greedy algorithms.

A cashier rings up a sale for $4.63 cents in U.S. currency. The customer pays with a $5 bill. The cashier would like to give the customer $0.37 in change using the fewest coins possible. The coins that can be used are quarters ($0.25), dimes ($0.10), nickels ($0.05), and pennies ($0.01). The cashier starts by selecting the coin of highest value less than or equal to $0.37, which is a quarter. This leaves $ 0.37 − $ 0.25 = $ 0.12 $ 0.37 − $ 0.25 = $ 0.12 . The cashier selects the coin of highest value less than or equal to $0.12, which is a dime. This leaves $ 0.12 − $ 0.10 = $ 0.02 $ 0.12 − $ 0.10 = $ 0.02 . The cashier selects the coin of highest value less than or equal to $0.02, which is a penny. This leaves $ 0.02 − $ 0.01 = $ 0.01 $ 0.02 − $ 0.01 = $ 0.01 . The cashier selects the coin of highest value less than or equal to $0.01, which is a penny. This leaves no remainder. The cashier used one quarter, one dime, and two pennies, which is four coins. Use this information to answer the following questions.

• Is the cashier’s approach an example of a greedy algorithm or a brute force algorithm? Explain how you know.
• The cashier’s solution is the best solution. In other words, four is the fewest number of coins possible. Is this consistent with the results of an algorithm of this kind? Explain your reasoning.
• The approach the cashier used is an example of a greedy algorithm, because the problem was approached in phases and the best choice was made at each phase. Also, it is not a brute force algorithm, because the cashier did not attempt to list out all possible combinations of coins to reach this conclusion.
• Yes, it is consistent. A greedy algorithm does not always yield the best result, but sometimes it does.

Your Turn 12.42

The traveling salesperson problem.

Now let’s focus our attention on the graph theory application known as the traveling salesperson problem (TSP) in which we must find the shortest route to visit a number of locations and return to the starting point.

Recall from Hamilton Cycles, the officer in the U.S. Air Force who is stationed at Vandenberg Air Force base and must drive to visit three other California Air Force bases before returning to Vandenberg. The officer needed to visit each base once. We looked at the weighted graph in Figure 12.219 representing the four U.S. Air Force bases: Vandenberg, Edwards, Los Angeles, and Beal and the distances between them.

Any route that visits each base and returns to the start would be a Hamilton cycle on the graph. If the officer wants to travel the shortest distance, this will correspond to a Hamilton cycle of lowest weight. We saw in Table 12.11 that there are six distinct Hamilton cycles (directed cycles) in a complete graph with four vertices, but some lie on the same cycle (undirected cycle) in the graph.

a → b → c → d → a

a → b → d → c → a

a → c → b → d → a

a → d → c → b → a

a → c → d → b → a

a → d → b → c → a

Since the distance between bases is the same in either direction, it does not matter if the officer travels clockwise or counterclockwise. So, there are really only three possible distances as shown in Figure 12.220.

The possible distances are:

396 + 410 + 106 + 159 = 1071 207 + 410 + 439 + 159 = 1215 396 + 439 + 106 + 207 = 1148 396 + 410 + 106 + 159 = 1071 207 + 410 + 439 + 159 = 1215 396 + 439 + 106 + 207 = 1148

So, a Hamilton cycle of least weight is V → B → E → L → V (or the reverse direction). The officer should travel from Vandenberg to Beal to Edwards, to Los Angeles, and back to Vandenberg.

Finding Weights of All Hamilton Cycles in Complete Graphs

Notice that we listed all of the Hamilton cycles and found their weights when we solved the TSP about the officer from Vandenberg. This is a skill you will need to practice. To make sure you don't miss any, you can calculate the number of possible Hamilton cycles in a complete graph. It is also helpful to know that half of the directed cycles in a complete graph are the same cycle in reverse direction, so, you only have to calculate half the number of possible weights, and the rest are duplicates.

In a complete graph with n n vertices,

• The number of distinct Hamilton cycles is ( n − 1 ) ! ( n − 1 ) ! .
• There are at most ( n − 1 ) ! 2 ( n − 1 ) ! 2 different weights of Hamilton cycles.

TIP! When listing all the distinct Hamilton cycles in a complete graph, you can start them all at any vertex you choose. Remember, the cycle a → b → c → a is the same cycle as b → c → a → b so there is no need to list both.

Example 12.43

Calculating possible weights of hamilton cycles.

Suppose you have a complete weighted graph with vertices N, M, O , and P .

• Use the formula ( n − 1 ) ! ( n − 1 ) ! to calculate the number of distinct Hamilton cycles in the graph.
• Use the formula ( n − 1 ) ! 2 ( n − 1 ) ! 2 to calculate the greatest number of different weights possible for the Hamilton cycles.
• Are all of the distinct Hamilton cycles listed here? How do you know? Cycle 1: N → M → O → P → N Cycle 2: N → M → P → O → N Cycle 3: N → O → M → P → N Cycle 4: N → O → P → M → N Cycle 5: N → P → M → O → N Cycle 6: N → P → O → M → N
• Which pairs of cycles must have the same weights? How do you know?
• There are 4 vertices; so, n = 4 n = 4 . This means there are ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 distinct Hamilton cycles beginning at any given vertex.
• Since n = 4 n = 4 , there are ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 possible weights.
• Yes, they are all distinct cycles and there are 6 of them.
• Cycles 1 and 6 have the same weight, Cycles 2 and 4 have the same weight, and Cycles 3 and 5 have the same weight, because these pairs follow the same route through the graph but in reverse.

TIP! When listing the possible cycles, ignore the vertex where the cycle begins and ends and focus on the ways to arrange the letters that represent the vertices in the middle. Using a systematic approach is best; for example, if you must arrange the letters M, O, and P, first list all those arrangements beginning with M, then beginning with O, and then beginning with P, as we did in Example 12.42.

Your Turn 12.43

The brute force method.

The method we have been using to find a Hamilton cycle of least weight in a complete graph is a brute force algorithm, so it is called the brute force method . The steps in the brute force method are:

Step 1: Calculate the number of distinct Hamilton cycles and the number of possible weights.

Step 2: List all possible Hamilton cycles.

Step 3: Find the weight of each cycle.

Step 4: Identify the Hamilton cycle of lowest weight.

Example 12.44

Applying the brute force method.

On the next assignment, the air force officer must leave from Travis Air Force base, visit Beal, Edwards, and Vandenberg Air Force bases each exactly once and return to Travis Air Force base. There is no need to visit Los Angeles Air Force base. Use Figure 12.221 to find the shortest route.

Step 1: Since there are 4 vertices, there will be ( 4 − 1 ) ! = 3 ! = 6 ( 4 − 1 ) ! = 3 ! = 6 cycles, but half of them will be the reverse of the others; so, there will be ( 4 − 1 ) ! 2 = 6 2 = 3 ( 4 − 1 ) ! 2 = 6 2 = 3 possible distances.

Step 2: List all the Hamilton cycles in the subgraph of the graph in Figure 12.222.

To find the 6 cycles, focus on the three vertices in the middle, B, E, and V . The arrangements of these vertices are BEV, BVE, EBV, EVB, VBE , and VEB . These would correspond to the 6 cycles:

1: T → B → E → V → T

2: T → B → V → E → T

3: T → E → B → V → T

4: T → E → V → B → T

5: T → V → B → E → T

6: T → V → E → B → T

Step 3: Find the weight of each path. You can reduce your work by observing the cycles that are reverses of each other.

1: 84 + 410 + 207 + 396 = 1097 84 + 410 + 207 + 396 = 1097

2: 84 + 396 + 207 + 370 = 1071 84 + 396 + 207 + 370 = 1071

3: 370 + 410 + 396 + 396 = 1572 370 + 410 + 396 + 396 = 1572

4: Reverse of cycle 2, 1071

5: Reverse of cycle 3, 1572

6: Reverse of cycle 1, 1097

Step 4: Identify a Hamilton cycle of least weight.

The second path, T → B → V → E → T , and its reverse, T → E → V → B → T , have the least weight. The solution is that the officer should travel from Travis Air Force base to Beal Air Force Base, to Vandenberg Air Force base, to Edwards Air Force base, and return to Travis Air Force base, or the same route in reverse.

Your Turn 12.44

Now suppose that the officer needed a cycle that visited all 5 of the Air Force bases in Figure 12.221. There would be ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 different arrangements of vertices and ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 distances to compare using the brute force method. If you consider 10 Air Force bases, there would be ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 different arrangements and ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 distances to consider. There must be another way!

The Nearest Neighbor Method

When the brute force method is impractical for solving a traveling salesperson problem, an alternative is a greedy algorithm known as the nearest neighbor method , which always visit the closest or least costly place first. This method finds a Hamilton cycle of relatively low weight in a complete graph in which, at each phase, the next vertex is chosen by comparing the edges between the current vertex and the remaining vertices to find the lowest weight. Since the nearest neighbor method is a greedy algorithm, it usually doesn’t give the best solution, but it usually gives a solution that is "good enough." Most importantly, the number of steps will be the number of vertices. That’s right! A problem with 10 vertices requires 10 steps, not 362,880. Let’s look at an example to see how it works.

Suppose that a candidate for governor wants to hold rallies around the state. They plan to leave their home in city A , visit cities B, C, D, E , and F each once, and return home. The airfare between cities is indicated in the graph in Figure 12.223.

Let’s help the candidate keep costs of travel down by applying the nearest neighbor method to find a Hamilton cycle that has a reasonably low weight. Begin by marking starting vertex as V 1 Figure 12.224. The lowest of these is $100, which is the edge between A and F .

Mark F as V 2 Figure 12.225. The lowest of these is $150, which is the edge between F and D .

Mark D as V 3 Figure 12.226. The lowest of these is $120, which is the edge between D and B .

So, mark B as V 4 Figure 12.227. The lower amount is $160, which is the edge between B and E .

Now you can mark E as V 5 Figure 12.228. Make a note of the weight of the edge from E to C , which is $180, and from C back to A , which is $210.

The Hamilton cycle we found is A → F → D → B → E → C → A . The weight of the circuit is $ 100 + $ 150 + $ 120 + $ 160 + $ 180 + $ 210 = $ 920 $ 100 + $ 150 + $ 120 + $ 160 + $ 180 + $ 210 = $ 920 . This may or may not be the route with the lowest cost, but there is a good chance it is very close since the weights are most of the lowest weights on the graph and we found it in six steps instead of finding 120 different Hamilton cycles and calculating 60 weights. Let’s summarize the procedure that we used.

Step 1: Select the starting vertex and label V 1 V 1 for "visited 1st." Identify the edge of lowest weight between V 1 V 1 and the remaining vertices.

Step 2: Label the vertex at the end of the edge of lowest weight that you found in previous step as V n V n where the subscript n indicates the order the vertex is visited. Identify the edge of lowest weight between V n V n and the vertices that remain to be visited.

Step 3: If vertices remain that have not been visited, repeat Step 2. Otherwise, a Hamilton cycle of low weight is V 1 → V 2 → ⋯ → V n → V 1 V 1 → V 2 → ⋯ → V n → V 1 .

Example 12.45

Using the nearest neighbor method.

Suppose that the candidate for governor wants to hold rallies around the state but time before the election is very limited. They would like to leave their home in city A , visit cities B , C , D , E , and F each once, and return home. The airfare between cities is not as important as the time of travel, which is indicated in Figure 12.229. Use the nearest neighbor method to find a route with relatively low travel time. What is the total travel time of the route that you found?

Step 1: Label vertex A as V 1 V 1 . The edge of lowest weight between A and the remaining vertices is 85 min between A and D .

Step 2: Label vertex D as V 2 V 2 . The edge of lowest weight between D and the vertices that remain to be visited, B, C, E , and F , is 70 min between D and F .

Repeat Step 2: Label vertex F as V 3 V 3 . The edge of lowest weight between F and the vertices that remain to be visited, B, C, and E , is 75 min between F and C .

Repeat Step 2: Label vertex C as V 4 V 4 . The edge of lowest weight between C and the vertices that remain to be visited, B and E , is 100 min between C and B .

Repeat Step 2: Label vertex B as V 5 V 5 . The only vertex that remains to be visited is E . The weight of the edge between B and E is 95 min.

Step 3: A Hamilton cycle of low weight is A → D → F → C → B → E → A . So, a route of relatively low travel time is A to D to F to C to B to E and back to A . The total travel time of this route is: 85 min + 70 min + 75 min + 100 min + 95 min + 90 min = 515 min or 8 hrs 35 min 85 min + 70 min + 75 min + 100 min + 95 min + 90 min = 515 min or 8 hrs 35 min

Your Turn 12.45

Check your understanding, section 12.9 exercises.

Travelling Salesman Problem

This humorously named problem refers to the following situation:

A travelling salesman , named Rover plans to visit each of n cities. He wishes to visit each city once and only once, arriving back to city from where he started. The distance between City i and City j is c ij . What is the shortest tour Rover can take?

If there are n cities, there are (n - 1)! possible ways for his tour. For example, if the number of cities to be visited is 5, then there are 4! different combinations. Such type of problems can be solved by the assignment method.

Let c ij be the distance (or cost or time) between City i to City j and

Use Horizontal Scrollbar to View Full Details

The following example will help you in understanding the travelling salesman problem of operation research.

Example: Travelling Salesman Problem

A travelling salesman, named Rolling Stone plans to visit five cities 1, 2, 3, 4 & 5. The travel time (in hours) between these cities is shown below:

How should Mr. Rolling Stone schedule his touring plan in order to minimize the total travel time , if he visits each city once a week?

"As every thread of gold is valuable, so is every minute of time." - John Mason

After applying steps 1 to 3 of the Hungarian method, we get the following assignments.

Use Horizontal Scrollbar to View Full Table.

Draw the minimum number of vertical and horizontal lines necessary to cover all the zeros in the reduced matrix.

Select the smallest element from all the uncovered elements. Subtract this smallest element from all the uncovered elements and add it to the elements, which lie at the intersection of two lines. Thus, we obtain another reduced matrix for fresh assignment. Repeating step 3 on the reduced matrix, we get the following assignments.

The above solution suggests that the salesman should go from city 1 to city 4, city 4 to city 2, and then city 2 to 1 (original starting point). The above solution is not a solution to the travelling salesman problem as he visits city 1 twice.

The next best solution can be obtained by bringing the minimum non-zero element, i.e., 1 into the solution. Please note that the value 1 occurs at four places. We will consider all the cases separately until the acceptable solution is obtained. To make the assignment in the cell (2, 3), delete the row & the column containing this cell so that no other assignment can be made in the second row and third column.

Now, make the assignments in the usual manner as shown in the following table.

He starts from city 1 and goes to city 4; from city 4 to city 2; from city 2 to city 3; from city 3 to city 5; from city 5 to city 1.

Substituting values from original table: 4 + 7 + 6+ 4 + 5 = 26 hours.

In this chapter, we focussed on a special type of transportation problem where the objective was to allocate n different facilities to n different tasks. Although an assignment problem can be formulated as a linear programming problem, it is solved by a special method known as Hungarian Method. If the number of persons is the same as the number of jobs, the assignment problem is said to be balanced. If the number of jobs is different from the number of persons, the assignment problem is said to be unbalanced. Some assignment problems entail maximizing the profit, effectiveness, or layoff of an assignment of persons to tasks or of jobs to machines. The Hungarian Method can also solve such problems. Further, the Hungarian method can also be utilized for solving crew assignment problem and the travelling salesman problem.

Share This Article

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Dynamic Programming or DP
• What is memoization? A Complete tutorial
• Dynamic Programming (DP) Tutorial with Problems
• Tabulation vs Memoization
• Optimal Substructure Property in Dynamic Programming | DP-2
• Overlapping Subproblems Property in Dynamic Programming | DP-1
• Steps for how to solve a Dynamic Programming Problem

Advanced Topics

• Bitmasking and Dynamic Programming | Set 1 (Count ways to assign unique cap to every person)
• Digit DP | Introduction
• Sum over Subsets | Dynamic Programming

Easy problems in Dynamic programming

• Count all combinations of coins to make a given value sum (Coin Change II)
• Subset Sum Problem
• Introduction and Dynamic Programming solution to compute nCr%p
• Cutting a Rod | DP-13
• Painting Fence Algorithm
• Longest Common Subsequence (LCS)
• Longest Increasing Subsequence (LIS)
• Longest subsequence such that difference between adjacents is one
• Maximum size square sub-matrix with all 1s
• Min Cost Path | DP-6
• Longest Common Substring (Space optimized DP solution)
• Count ways to reach the nth stair using step 1, 2 or 3
• Count Unique Paths in matrix
• Unique paths in a Grid with Obstacles

Medium problems on Dynamic programming

• 0/1 Knapsack Problem
• Printing Items in 0/1 Knapsack
• Unbounded Knapsack (Repetition of items allowed)
• Egg Dropping Puzzle | DP-11
• Word Break Problem | DP-32
• Vertex Cover Problem (Dynamic Programming Solution for Tree)
• Tile Stacking Problem
• Box Stacking Problem | DP-22
• Partition problem | DP-18

Travelling Salesman Problem using Dynamic Programming

• Longest Palindromic Subsequence (LPS)
• Longest Common Increasing Subsequence (LCS + LIS)
• Find all distinct subset (or subsequence) sums of an array
• Weighted Job Scheduling
• Count Derangements (Permutation such that no element appears in its original position)
• Minimum insertions to form a palindrome | DP-28
• Ways to arrange Balls such that adjacent balls are of different types

Hard problems on Dynamic programming

• Palindrome Partitioning
• Word Wrap Problem
• The Painter's Partition Problem
• Program for Bridge and Torch problem
• Matrix Chain Multiplication | DP-8
• Printing brackets in Matrix Chain Multiplication Problem
• Maximum sum rectangle in a 2D matrix | DP-27
• Maximum profit by buying and selling a share at most k times
• Minimum cost to sort strings using reversal operations of different costs
• Count of AP (Arithmetic Progression) Subsequences in an array
• Introduction to Dynamic Programming on Trees
• Maximum height of Tree when any Node can be considered as Root
• Longest repeating and non-overlapping substring
• Top 20 Dynamic Programming Interview Questions

Travelling Salesman Problem (TSP):  

Given a set of cities and the distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle. 

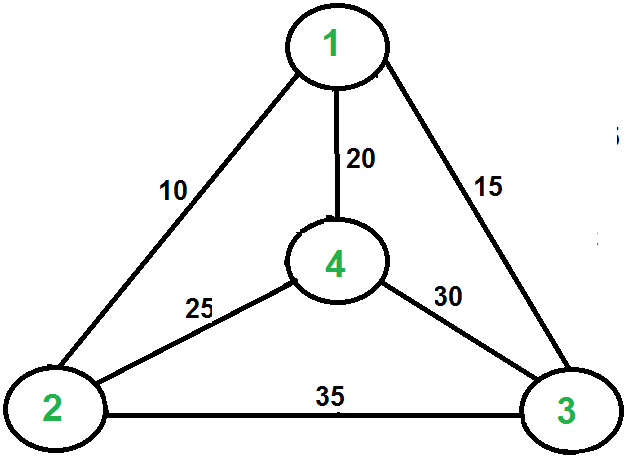
For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time know solution for this problem. The following are different solutions for the traveling salesman problem. 

Naive Solution:  

1) Consider city 1 as the starting and ending point.

2) Generate all (n-1)! Permutations of cities. 

3) Calculate the cost of every permutation and keep track of the minimum cost permutation. 

4) Return the permutation with minimum cost. 

Time Complexity: ?(n!) 

Dynamic Programming:  

Let the given set of vertices be {1, 2, 3, 4,….n}. Let us consider 1 as starting and ending point of output. For every other vertex I (other than 1), we find the minimum cost path with 1 as the starting point, I as the ending point, and all vertices appearing exactly once. Let the cost of this path cost (i), and the cost of the corresponding Cycle would cost (i) + dist(i, 1) where dist(i, 1) is the distance from I to 1. Finally, we return the minimum of all [cost(i) + dist(i, 1)] values. This looks simple so far. 

Now the question is how to get cost(i)? To calculate the cost(i) using Dynamic Programming, we need to have some recursive relation in terms of sub-problems. 

Let us define a term C(S, i) be the cost of the minimum cost path visiting each vertex in set S exactly once, starting at 1 and ending at i . We start with all subsets of size 2 and calculate C(S, i) for all subsets where S is the subset, then we calculate C(S, i) for all subsets S of size 3 and so on. Note that 1 must be present in every subset.

Below is the dynamic programming solution for the problem using top down recursive+memoized approach:-

For maintaining the subsets we can use the bitmasks to represent the remaining nodes in our subset. Since bits are faster to operate and there are only few nodes in graph, bitmasks is better to use.

For example: –  

10100 represents node 2 and node 4 are left in set to be processed

010010 represents node 1 and 4 are left in subset.

NOTE:- ignore the 0th bit since our graph is 1-based

Time Complexity : O(n 2 *2 n ) where O(n* 2 n) are maximum number of unique subproblems/states and O(n) for transition (through for loop as in code) in every states.

Auxiliary Space: O(n*2 n ), where n is number of Nodes/Cities here.

For a set of size n, we consider n-2 subsets each of size n-1 such that all subsets don’t have nth in them. Using the above recurrence relation, we can write a dynamic programming-based solution. There are at most O(n*2 n ) subproblems, and each one takes linear time to solve. The total running time is therefore O(n 2 *2 n ). The time complexity is much less than O(n!) but still exponential. The space required is also exponential. So this approach is also infeasible even for a slightly higher number of vertices. We will soon be discussing approximate algorithms for the traveling salesman problem.

Next Article: Traveling Salesman Problem | Set 2  

References:  

http://www.lsi.upc.edu/~mjserna/docencia/algofib/P07/dynprog.pdf  

http://www.cs.berkeley.edu/~vazirani/algorithms/chap6.pdf  

Please Login to comment...

Similar reads.

• Dynamic Programming

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

What is a Travelling Salesman Problem (TSP)? Explained!

• Author: Diksha Bhandari
• Read Time: 9 min
• Published: September 14, 2023
• Last Update: November 8th, 2023

Table of Contents

• Driver Behaviour
• Last Mile Delivery
• Asset Tracking
• Dispatch Management
• Fuel Management
• Route Optimisation
• Electric Vehicle
• Roster Management
• Vehicle Tracking
• TrackoMile Industries
• TrackoBit Industries
• Sensor Integration
• GPS Trackers and Hardware
• Tech and Beyond
• TrackoField
• What's New
• Employee Management
• Field Sales And Service
• Task and Workflow
• GPS Software
• Lead Management
• Fleet Management
• Leave And Attendance
• Video telematics
• TrackoField Industries
• Route Planning

Want to know what a travelling salesman problem (TSP) is? Need solutions to real-life TSP challenges. Learn here. 

Do you also look for the shortest route on Google Maps before embarking on a trip?

I am sure, you know multiple routes to reach the office, the mall, or your desired location, but checking on the internet before leaving home has become a ritual. It becomes all the more important to refer to maps when you have to pick up friends or colleagues along the way.

‘ADD STOPS’

Yes, you are right! 💯

That’s what solving the TSP challenge using software means!

What is a Travelling Salesman Problem (TSP)?

The traveling salesman problem is the popular combinatorial optimisation challenge in mathematics and computer science. The prime objective of the problem is to determine the shortest possible route a salesperson must take to cover a set of locations in one go and then return to the starting point.

Addressing travelling salesman challenges and their optimisation are more relevant in this time and age, especially in the supply chain, logistics and delivery space.

TSP may result in delayed deliveries and slimming profits as it’s not easy for delivery agents to choose the most viable and cost-effective route in real-time.

What are Traveling Salesman Problem Challenges to Solve?

When a salesperson is in the field hopping from one client site to another, finding out the best and the shortest route is an added pressure on the agent. In today’s day and age, distance isn’t the only factor that defines efficiency. There are several factors, such as time, fuel consumption, capacity, etc. that together define efficiency.

However, addressing the travelling salesman challenges involves mitigating a few unavoidable challenges along the way that field agents face themselves.

1. Time Constraints

Sales agents often have a tight schedule with multiple deliveries to make with a short TAT. Similarly, in TSP, optimising routes to minimise travel time is a fundamental challenge.

2. Last-minute Changes

Eleventh-hour changes are not a new concept for salespeople. They encounter urgent visits and last-minute cancellations a lot. Similarly, TSP solutions must be adaptable to handle dynamic scenarios and route modifications.

3. Resource Efficiency

Just as salespersons aim at reducing fuel costs and ensuring on-time deliveries, TSP solutions such as TrackoMile must strive for resource optimisation by reducing travel distances and delivery TAT.

4. Objective Diversification

While solving the travelling salesman problem (TSP) , optimising multiple objectives such as cost, time, and environmental factors adds complexity as solutions need to balance conflicting goals.

5. Combinatorial Complexity

TSP is a combinatorial optimisation problem, which means it involves complicated mathematical calculations with numerous variables. Sometimes, complex scenarios get further intricate as multiple variables are involved.

6. Adaptability and Scalability

Similarly, how sales agents adjust to the routes on the fly, the route algorithm must be flexible and responsive to real-time changes such as spiking volumes, vehicle breakdown or traffic slow down. A TSP solution must have a good appetite to handle large datasets and complex networks.

Also Read 4 Key Solutions for Fuel Management System 2023

Top 5 Solutions to The Travelling Salesman Problem

The traveling salesman problem solutions offer various trade-offs between computational intricacies and the quality of the resolution, allowing practitioners to choose the best-suited approach based on their needs and problems.

Here are the Top 5 solutions to the Traveling Salesman Problem (TSP) :

1. Brute Force Algorithm

The Brute Force algorithm is a straight approach to solving the Traveling Salesman Problem (TSP). It systematically explores all possible routes to identify the shortest one among them all. While it guarantees an optimal solution, its downside lies in its major time complexity, making it practical only for small TSP challenges.

2. Nearest Neighbour Algorithm

The Nearest Neighbour method is the simplest heuristic for the TSP. It starts from the first location and repeatedly selects the closest unvisited location to form a tour. Although it is quick to implement this method, it may always yield the optimal solution for it prioritises proximity over other factors.

3. Genetic Algorithm

This technique or method draws inspiration from nature itself. They evolve TSP solutions through selection, crossovers and mutation. They pick the best routes and mix them up. This creates new routes that might be even better. Then, they keep the best ones and repeat the mixing and picking process. Survival of the fittest in the true sense.

4. Ant Colony Optimisation (ACO)

Ants have a tendency to leave pheromones on the shorter routes they find, calling fellow ants on the same route. They keep leaving more pheromones on the shorter routes they find. Over time, the collective behaviour of the ants causes them to converge on the shortest route. Inspired by the nature of ants, ACO finds the shortest route by analysing the trails of data left by artificial ants based on the strength of these data trails.

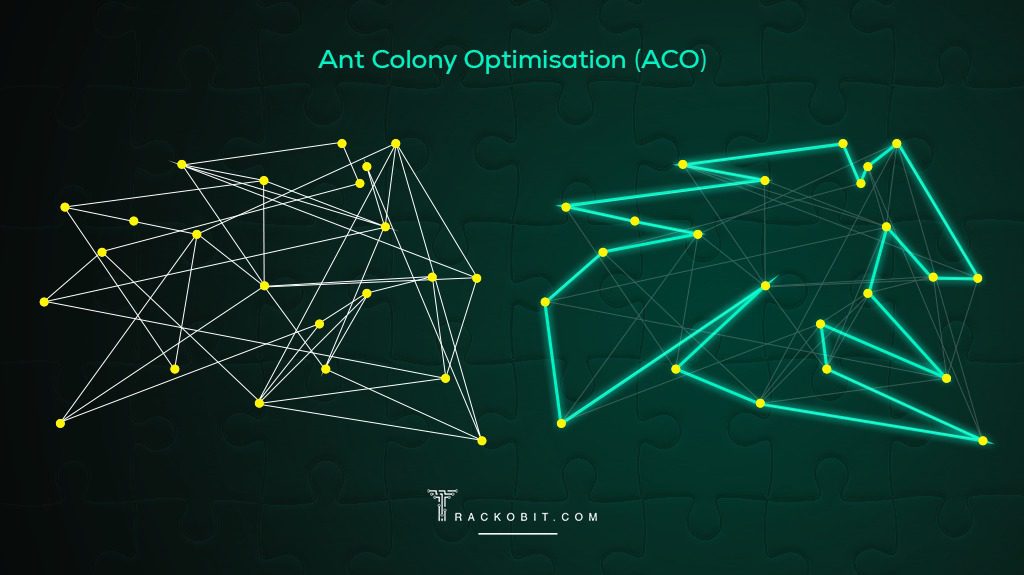
5. Dynamic Programming

Dynamic Programming is like solving a puzzle, step-by-step, by breaking it into smaller pieces. In TSP challenges, it finds the best route to visit all locations. It begins with figuring out the shortest route between two locations; then it builds on that to find ways to more locations. It’s a smart TSP solution for small scenarios but may require significant memory resources for larger and more complex problems.

What Are Real-world Travelling Salesman Problem Applications?

The Traveling Salesman Problem (TSP) has a wide array of applications across various domains due to its relevance in optimising routes and sequences. Here are several crucial real-word TSP applications and implementations in the real world.

1. TSP implementation in Logistics and Delivery Services

The logistics and supply chain sectors have the widest TSP applications.

• Courier, Express & Parcel : Companies like FedEx, UPS, and DHL rely on TSP algorithms to optimise delivery routes for their fleet of delivery trucks. By finding the most efficient sequence of stops, they minimise fuel consumption , reduce delivery TAT, and save on operational overheads too.
• On-demand Delivery : Food delivery companies, instant grocery delivery apps and at-home appointment platforms like Swiggy, BlinkIt and UrbanCompany, respectively, leverage TSP solutions to ensure timely delivery. Enhancing the customer experience and increasing the number of deliveries each rider can make.

2. TSP Applications in Transportation and Urban Planning Waste collection routes, Traffic light synchronisation, optic cable installation, etc. are some areas where TSP Solutions works like a knight in shining armour. Other real-world TSP applications include

• Public Transport : City planners and public transport agencies use TSP principles to design bus, tram and train routes that reduce travel for passengers.
• Emergency Service Dispatch : Ambulance services, Police PCR vans employ TSP algorithms to dispatch vehicles quickly and efficiently in response to emergency calls. Finding the shortest route to reach the incident location can save lives.
• Urban Mobility Solution : In the era of ride-sharing and on-demand mobility apps like Uber, Ola, Lyft, etc., real-world TSP applications become prominent. TSP solutions optimise the route to destinations, ensuring quick and cost-effective transportation.

Other significant real-life applications of the Travelling Salesman Problem are

• TSP in Healthcare and Medical Research – for DNA sequencing and understanding genetic patterns and diseases.
• TSP in Manufacturing and Production – In circuit board manufacturing and job scheduling of technicians.
• TSP in Robotics and Autonomous Vehicles -Self-driving cars and drones use TSP-like algorithms for efficient navigation.

Solving the Travelling Salesman Problem – Last Mile Delivery Route Optimisation

Route optimisation is the key to efficient last-mile delivery . In order to attain flawless route optimisation, the software must solve the traveling salesman problem every step of the way.

Why it’s essential to solve TSP for Last Mile Delivery?

In simple and minimal words, solving TSP problems helps in many ways:

• Saves Time : It makes deliveries faster, so your customers get orders sooner.
• Customer Satisfaction : Fast deliveries give you an edge over the competition and enhance customer experience too.
• Saves Money : It reduces fuel wastage and vehicle wear, making deliveries cheaper.
• Environment Friendly : It lowers pollution by using fewer vehicles and shorter routes.
• Happy Staff: Drivers and dispatchers have less stress and can finish their work faster.

How do we solve the travelling salesman problem for last-mile delivery?

Solving TSP challenges for Last-mile delivery is like solving a big jigsaw puzzle. There are a hundred thousand addresses to visit daily. The software must find the shortest and most optimised route to them and come back to the starting point at the end.

• Our route optimisation software , TrackoMile, leverages capacity management , routing algorithms and robust rule engines to present the most optimal combination of delivery addresses. Thereby giving the most optimally planned routes or trips.
• All delivery managers have to do is upload the CSV file of the addresses or integrate TrackoMile to their CRM to fetch the delivery addresses. Now trip allocation, route optimisation, dispatch and everything else happen in a few clicks.
• ETA when the delivery is en route, POD when the order is delivered successfully, and trip analysis, are added features to simplify overall operations.

The Vehicle Routing Problem is very similar to TSP, with wide applications in logistics, delivery services and transportation. While TSP focuses on finding the shortest route for a single traveller visiting various locations, VRP deals with multiple vehicles serving multiple customers, considering added constraints like vehicle capacity, TATs and more.

How Can AI Help in Solving Traveling Salesman Problem (TSP)?

AI or Artificial Intelligence are becoming the driving force for business growth across various industrial sectors. AI particularly aids in solving the Traveling Salesman Problem(TSP) in the logistics and delivery sector by employing advanced algorithms and techniques. What are a few tricks up AI’s sleeves that help in automating TSP resolution? Let’s find out!

1. Advanced Algorithms

AI algorithms such as Genetic Algorithms, ACO, simulated annealing and a few others mentioned above, tackle complex Travelling Salesman Problem scenarios.

2. Machine Learning

Gathering information from historical data and optimising routes based on real-time insights is what AI is best for. Machine learning models are trained to adapt to changing conditions, like traffic, weather and delivery constraints, to provide a more accurate plan of action.

3. Parallel Computing

AIi enables the use of a parallel computing process, which means solving multiple segments of TSP simultaneously. This accelerates the problem-solving process for large-scale challenges.

4. Heuristic Improvement

TSP Heuristics powered by AI can groom initial solutions, gradually improving their results over time. These heuristics can be applied iteratively by AI to reach better results.

5. Hybrid Approaches

Applying hybrid algorithms is not a new technique to refine techniques and produce more accurate results. AI on top of it singles out data-oriented combinations that work the best in varied use cases.

Wrapping Up!

The travelling salesman problem’s importance lies in its real-world applications. Whether optimising delivery routes, planning manufacturing processes or organising circuit board drilling, finding the most efficient way to cover multiple locations is crucial to minimise costs and save time.

The TSP problems have evolved over the years, and so have TSP algorithms, heuristics and solutions. With the advent of advanced technologies such as GPS and machine learning, TSP continues to adapt and find new applications in emerging fields, cementing its status as a fundamental problem in optimization theory and a valuable tool for various industries. Mobility automation software like Trackobit, TrackoMile and TrackoField resort to TSP heuristics to solve challenges along the way.

Read Blog – Best Delivery Route Planner Apps for 2023

Traveling Salesman Problem FAQs

What is tsp.

TSP is an abbreviation for Traveling Salesman Problem. It’s the routing problem that deals with finding the shortest route to travel to a combination of locations in the most optimal manner.

Is Travelling Salesman Problem Solvable?

Yes, the Traveling Salesman Problem (TSP) is solvable, but the time to find the solution can grow proportionately with an increase in the number of locations. With the evolution of travelling salesman problem applications, various TSP algorithms and heuristics, their hybrids have also emerged.

Wh at is the objective of TSP?

The objective of the Traveling Salesman Problem (TSP) is to find the shortest possible route that covers all given locations or waypoints and comes back to the starting point with the least resource utilisation.

Diksha Bhandari

Currently creating SaaSy content strategies for TrackoBit and TrackoField, this content professional has dedicated a decade of her life to enriching her portfolio and continues to do so. In addition to playing with words and spilling SaaS, she has a passion for traveling to the mountains and sipping on adrak wali chai.

• Author Showcase
• All Blog Post

Never Miss a Beat

Related Blog

Top 12 Google Map Alternatives – Offering Precise Navigation

Explore our best picks for 12 free Google map alternatives that offer accurate and secure location and navigational solutions. 

Food Delivery Trends to Watch in 2024 & Beyond

Food and technology are both revolving along with consumer demands. Here are some of the food delivery trends to watch in 2024.

Biofuel – An Alternative to Fossil Fuels in Transportation | G20

Transportation industries are moving towards a greener future through the sustainable use of biofuels like Ethanol — discussed in the G20 2023 summit.

Top 10 Navigation Apps for Android and iOS | 2024

Discover the 10 best navigation apps in 2024 that offer personalised navigation just like Sherpas (experienced guides of Himalayan terrain) do.

Thank you for reaching out! We'll speak to you soon.

In the meantime, why not find out more about us, explore our products, or visit our blog?

Stay Updated on tech, telematics and mobility. Don't miss out on the latest in the industry.

Cookie Consent

We use cookies to enhance and personalize your browsing experience. By continuing to use our website, you agree to our Privacy Policy.

• Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

Solving Dynamic Traveling Salesman Problem

• First Online: 09 July 2023

Cite this chapter

• Weiqi Li 2  

Part of the book series: Synthesis Lectures on Operations Research and Applications ((SLORA))

The rapid development in the applications in which data flow are considered to be time-dependent has caused an increasing interest in the dynamic optimization problems. The goal of an optimization search system for a dynamic optimization problem is to continuously track and adapt to the changing problem through time and to find the currently best solution quickly. This chapter describes how to apply the ABSS to solve the dynamic TSP.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as EPUB and PDF
• Read on any device
• Instant download
• Own it forever
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Branke, J. (2002). Evolutionary Optimization in Dynamic Environments . Springer.

Book   MATH   Google Scholar  

Branke, J., Kaussler, T., Smidt, C., & Schmeck, H. (2000). A Multi-population Approach to Dynamic Optimization Problems. In: Parmee, I.C. (eds) Evolutionary Design and Manufacture , pp. 299–307. Springer, London. https://doi.org/10.1007/978-1-4471-0519-0_24

Burkard, R. E., Deineko, V. G., van Dal, R., van der Veen, J. A. A., & Woeginger, G. J. (1998). Well-solvable special cases of the traveling salesman problem: A survey. SIAM Review, 40 (3), 496–546. https://doi.org/10.1137/S0036144596297514

Article   MathSciNet   MATH   Google Scholar  

Cheong, T., & White, C. C. (2012). Dynamic traveling salesman problem: Value of real-time traffic information. IEEE Transactions on Intelligent Transportation Systems, 13 (2), 619–630. https://doi.org/10.1109/TITS.2011.2174050

Article   Google Scholar  

Corne, D. W., Oates, M. J., & Smith, G. D. (2001). Telecommunications Optimization: Heuristic and Adaptive Techniques . John Wiley & Sons.

Book   Google Scholar  

Eychelhof, C. J., & Snoek, M. (2002). Ant systems for a dynamic TSP: ants caught in a traffic jam. In: Proceedings of the Third International Workshop on Ant Algorithms , pp. 88–99.

Google Scholar  

Floudas, C. A., Pardalos, P. M., Adjiman, C. S., Esposito, W. R., Gümüs, Z. H., Harding, S. T., Klepeis, J. L., Meyer, C. A., & Schweiger C. A. (1999). Dynamic optimization problems. In: Handbook of Test Problems in Local and Global Optimization, Nonconvex Optimization and Its Applications , 33, Springer, Boston.

Gambardella, L., Taillard, É., & Dorigo, M. (1999). Ant colonies for the quadratic assignment problem. Journal of the Operational Research Society , 50, 167–176 (1999). https://doi.org/10.1057/palgrave.jors.2600676

Guntsch, M., & Middendorf, M. (2001). Pheromone modification strategies for ant algorithms applied to dynamic TSP. In: Proceedings of Workshops on Applications of Evolutionary Computing, EvoWorkshops 2001 . LNCS , vol. 2037, pp. 213–222, Springer, Berlin. https://doi.org/10.1007/3-540-45365-2_22

Guntsch, M., & Middendorf, M. (2002). Applying population based ACO to dynamic optimization problems. In: Dorigo, M., Di Caro, G., Sampels, M. (eds) Ant Algorithms. ANTS 2002 . LNCS , vol. 2463, pp. 111–122, Springer, Berlin. https://doi.org/10.1007/3-540-45724-0_10

Kang, L., Zhou, A., McKay, B., Li Y., & Kang, Z. (2004). Benchmarking algorithms for dynamic traveling salesman problem. In: Proceedings of the 2004 Congress on Evolutionary Computation , pp. 1286–1292. https://doi.org/10.1109/CEC.2004.131045 .

Li, C., Yang, M., & Kang, L. (2006). A new approach to solving dynamic traveling salesman problems. In: Simulated Evolution and Learning. SEAL 2006 . LNCS , vol. 4247, pp. 236–243, Springer, Berlin. https://doi.org/10.1007/11903697_31

Mavrovouniotis, M., Ellinas, G., Bonilha, I.S., Müller, F.M., & Polycarpou, M. (2023). Applying the population-based ant colony optimization to the dynamic vehicle routing problem. In: Biswas, A., Kalayci, C.B., Mirjalili, S. (eds) Advances in Swarm Intelligence. Studies in Computational Intelligence , vol. 1054, pp. 369–384, Springer, Cham. https://doi.org/10.1007/978-3-031-09835-2_20

Morrison, R. W. (2004). Designing Evolutionary Algorithms for Dynamic Environments . Springer.

Morrison, R. W., & De Jong, K. A. (2004). Triggered hypermutation revisited. In: Proceedings of 2000 Congress on Evolutionary Computation , pp. 1025–1032.

Powell, W. B., Jaillet, P., & Odoni, A. (1995). Stochastic and dynamic networks and routing. Handbooks in Operations Research and Management Science, 8 , 141–295. https://doi.org/10.1016/s0927-0507(05)80107-0

Psaraftis, H. N. (1988). Dynamic vehicle routing. In B. L. Golen & A. A. Assad (Eds.), Vehicle Routing: Methods and Studies (pp. 223–248). Elsevier.

Simöes, A. (2001). Evolutionary Algorithms in Dynamic Optimization Problems . LAP Lamber Academic Publishing.

Simöes, A., & Costa, E, (2003). An immune system-based genetic algorithm to deal with dynamic environments: diversity and memory. In: Proceedings of International Conference on Neural Networks and genetic Algorithms , pp. 168–174

Stützle, T., & Hoos, H. (1998). Improvements on the ant-system: introducing the MAX-MIN ant system. In: Artificial Neural Nets and Genetic Algorithms , pp. 245–249, Springer, Vienna. https://doi.org/10.1007/978-3-7091-6492-1_54

Tfaili, W., & Siarry, P. (2008). A new charged ant colony algorithm for continuous dynamic optimization. Applied Mathematics and Computation, 197 (2), 604–613. https://doi.org/10.1016/j.amc.2007.08.087

Tinos, R., & Yang, S. (2007). A self-organizing random immigrants genetic algorithm for dynamic optimization problems. Genetic Programming and Evolvable Machines, 8 (3), 255–286. https://doi.org/10.1007/s10710-007-9024-z

Ursem, R. K. (2000). Multinational GA: optimization techniques in dynamic environments. In: Proceedings of the Second Genetic and Evolutionary Computation Conference, pp. 19–26, Morgan Kaufman, San Francisco

Weicker, K. (2003). Evolutionary Algorithms and Dynamic Optimization Problems . Der Andere Verlag.

MATH   Google Scholar  

Wineberg, M., & Oppacher, F. (2000). Enhancing the GA’s ability with dynamic environments. In: Proceedings of Genetic and Evolutionary Computation Conference, GEC2005 , pp. 3–10

Yang, S. (2008). Genetic algorithms with memory and elitism based immigrants in dynamic environments. Evolutionary Computation, 16 (3), 385–416. https://doi.org/10.1162/evco.2008.16.3.385

Yang, S., Ong, S. Y., & Jin, Y. (2007). Evolutionary Computation in Dynamic and Uncertain Environments . Springer.

Yang, S., & Yao, X. (2008). Population-based incremental learning with associative memory for dynamic environments. IEEE Transactions on Evolutionary Computation, 12 (5), 542–561. https://doi.org/10.1109/TEVC.2007.913070

Younes, A., Areibi, S., Calamai, P., & Pasir, O. (2008). Adapting genetic algorithms for combinatorial optimization problems in dynamic environments. In: Advances in Evolutionary Algorithms , pp. 207–230, InTech, Croatia.

Download references

Author information

Authors and affiliations.

School of Management, University of Michigan, Flint, MI, USA

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Weiqi Li .

Rights and permissions

Reprints and permissions

Copyright information

© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this chapter

Li, W. (2024). Solving Dynamic Traveling Salesman Problem. In: The Traveling Salesman Problem. Synthesis Lectures on Operations Research and Applications. Springer, Cham. https://doi.org/10.1007/978-3-031-35719-0_7

Download citation

DOI : https://doi.org/10.1007/978-3-031-35719-0_7

Published : 09 July 2023

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-35718-3

Online ISBN : 978-3-031-35719-0

eBook Packages : Synthesis Collection of Technology (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research