art of problem solving least common multiple

Find anything you save across the site in your account

Richard Rusczyk’s Worldwide Math Camp

By Ingfei Chen

At the start of a YouTube video titled “ Art of Problem Solving: Least Common Multiple ,” Richard Rusczyk invites viewers to play a game. Every twenty-four seconds, we’re supposed to clap; every forty-five seconds, we’re supposed to jump. The challenge is to keep going until we clap and jump at the same time. Rusczyk, who is dark-haired, clean-shaven, and boyish, gestures to a digital timer that appears in a corner of the screen. He starts the clock, stares at it, and fidgets. “Um, how long is this gonna take?” he asks, rolling his eyes like a teen-ager. “I hate waiting.”

When the timer hits twenty-four seconds, Rusczyk claps. When it reaches forty-five, he jumps. Meanwhile, on a digital blackboard, he starts trying to figure out when the clap and the jump will coincide. Over the course of a continuous seven-minute take, Rusczyk jumps and claps at the right times while scribbling equations. First, he tries writing out multiples of twenty-four, but gets bored. Then he tries expressing twenty-four and forty-five as products of their prime-number components: twenty-four is 2³ x 3¹, and forty-five is 3² x 5¹. “This is gonna work,” he says, clapping. Just as he concludes that it will take three hundred and sixty seconds for the clap and jump to converge, he claps and leaps simultaneously; as it happens, the timer has reached three hundred and sixty. It’s an exuberant, precise performance intended for middle-school kids, or younger ones, who are capable of doing advanced math.

Rusczyk, who lives near San Diego, founded Art of Problem Solving—or AoPS—eighteen years ago as a resource for budding math prodigies. Exceptionally gifted young math students often find classroom math unbearably easy and tedious; their parents can have difficulty obtaining sufficiently stimulating lessons. By offering online instruction in math that’s more complex than what’s in standard gifted-and-talented programs, AoPS has become a lifeline for math whizzes. Its free online forums also serve as a vital social network, allowing math prodigies to connect with kindred spirits every day.

Rusczyk began posting free videos more than a decade ago; he ad-libs without a written script. He made “Least Common Multiple,” with its quirky dramatization of a humdrum numerical concept, in 2011, at age forty. Some of his videos have garnered hundreds of thousands of views; occasionally, they feature his alter ego, a gravelly voiced character in dark shades and a black hoodie. Onscreen, Rusczyk conveys a playful, experimental fearlessness that sweeps young learners along. “It’s a slightly intangible quality that some people have, and he’s got it in spades,” the mathematician Sam Vandervelde, who is the head of Proof School, a private, math-centric liberal arts academy in San Francisco, told me.

Kristen Chandler, a former math teacher who is the executive director of MathCounts , a nonprofit that runs a popular middle-school math contest series, told me that Rusczyk is “a rock star at our competitions.” (Along with Raytheon Technologies, the Department of Defense STEM , and others, AoPS is a sponsor of the MathCounts program.) Pre-pandemic, Rusczyk attended the MathCounts national finals each May as an invited speaker; Chandler recalled how contestants and parents flocked to get his autograph and take selfies with him. One competitor asked Rusczyk to sign his forehead with a marker.

For years, AoPS grew gradually. It released print textbooks, Math Olympiad-prep materials, and an accredited online curriculum, including a free adaptive learning system containing thousands of hard math problems. In 2012, it began rolling out Beast Academy, an elementary-school curriculum in which advanced mathematical concepts are communicated to young math geeks by wisecracking comic-book monsters. It also opened ten brick-and-mortar learning centers across the country. By 2019, about thirty-six thousand math students from around the world were using its paid online curriculum or in-person courses, and tens of thousands more were consulting its textbooks for independent study.

In the spring of 2020, when schools shuttered , the company’s Web site traffic jumped five- to six-fold, and enrollments doubled. AoPS’s hundred employees began telecommuting, except for Rusczyk and four warehouse workers. On nights or weekends, Rusczyk and his wife, Vanessa, would go into the empty company headquarters—a two-story office building in the suburb of Rancho Bernardo—to help fill book orders. One Sunday when he was in the office, we connected over Zoom. He was dressed in a short-sleeved blue plaid shirt. Five feet seven, with cropped hair, Rusczyk has a quick, self-deprecating wit and sometimes laughs like a kid, almost doubled over. On a brief tour, he showed me stacks of book boxes in the warehouse and framed illustrations of Beast Academy monsters. In a dim hallway, the overhead fluorescent lighting had stopped working, except for one eerily flickering panel. “This is where the zombies are going to get me in the zombie apocalypse,” he said, grinning. (He read a lot of sci-fi and fantasy as a child.)

Now fifty, Rusczyk bonds easily with math-obsessed kids because he used to be one of them. Growing up, he was fast with calculations and showed a brilliant, intuitive grasp of geometric relationships. He had a competitive streak, and won many math competitions. But, at the same time, he experienced deflating setbacks that helped dissuade him from the academic pursuit of mathematics. He loved math—it had taught him about resilience, creativity, and the joys of finding one’s tribe. Still, he faced a conundrum: If you’re a math prodigy who doesn’t want to become a mathematician, what do you do with your life? Art of Problem Solving was his solution.

Rusczyk was born in Idaho Falls. He and his younger sister attended elementary schools in half a dozen states as their father, a U.S. naval officer and nuclear engineer, moved from one base to the next. Small but naturally athletic, Rusczyk played basketball and spouted pro baseball statistics—these “got him into numbers,” his mother, Claire, a former grade-school teacher, told me. In 1983, Claire read a newspaper article about the launch of the MathCounts program. Rusczyk, who was in seventh grade, signed up and did well; he loved being surrounded by dozens of teens who got a kick out of wrestling with numbers. Two years later, after the family had settled in Decatur, Alabama, he placed twenty-fourth at the MathCounts national finals.

Rusczyk became the star of his high school’s math team, which travelled to competitions around the Southeast. He also participated individually in the American Mathematics Competitions, a rigorous series organized by the Mathematical Association of America (M.A.A.). The contests built up to the U.S.A. Mathematical Olympiad, which back then was a five-question, three-and-a-half-hour examination. Rusczyk played tennis and ran cross-country, but he relished math and the company of his math buddies even more. His bookshelves were filled with math-contest ribbons and trophies. “I was definitely a trophy hunter,” he said. He spent hours practicing with old math-contest problems in his bedroom.

In June, 1987, after his sophomore year, he was invited to the M.A.A.’s Mathematical Olympiad Summer Program, reserved for those who’d placed in the top tier of the U.S.A. Mathematical Olympiad. The program was an intensive, monthlong math boot camp, held each year at either West Point or the Naval Academy, in Annapolis. (A redesigned program is now hosted by Carnegie Mellon University.) At West Point, Rusczyk was one of two dozen boot campers, nearly all boys. They stayed in spartan dorm rooms and were rousted early by the bugle call of reveille. Largely based on three exams in the first week—each roughly four hours long—six students would be chosen to represent the U.S. at the International Mathematical Olympiad, or I.M.O., in July.

Rusczyk arrived excited, expecting that he would be able to hold his own. On the first day, a professor stood at a blackboard and wrote “Counting” in chalk; the topic—“falling factorials”—was unfamiliar. Within minutes, Rusczyk was bewildered. It quickly became obvious that he wasn’t even close to being the brightest kid in the room. It was an unsettling feeling. Other students absorbed the math like sponges; some were clearly geniuses. Rusczyk couldn’t solve a single problem on the gruelling practice exams. Being outgunned by his cerebral classmates was inspiring but also terrifying. “I shut down by the end of the first week,” he recalled.

Still, the group was friendly, bantering over board games and Ultimate Frisbee. Rusczyk, who had brought his basketball, nimbly dribbled around the other campers. He formed strong friendships, including with Vandervelde, a fellow-Southerner. He noticed that Vandervelde and other top students—among them, the future mathematician and writer Jordan Ellenberg—appeared enthralled with pondering abstract numerical concepts and questions for their own sakes. Rusczyk realized that, for him, the appeal of math lay more in competition and camaraderie.

Rusczyk didn’t make the I.M.O. team; later he learned that a few other students were also struggling. The next summer, he attended the boot camp again, this time in Annapolis, and was still frequently perplexed. Nevertheless, he kept studying; in his senior year of high school, he began working through some mathematical proofs, attaining a more genuine grasp of the concepts. He graduated as valedictorian, was a winner of the U.S.A. Mathematical Olympiad—at that time, eight medals were awarded each year—and returned to the boot camp for a third summer. Although he didn’t qualify for the I.M.O. team that year, either—Vandervelde and Ellenberg did—he was picked as an alternate. He left the camp early after falling ill, ranked as one of the top eight high-school math students in the nation.

Rusczyk went to Princeton, famed for its powerhouse math department. But he was burned out. The boot camps had left him certain that he lacked the creativity to solve the great abstract mysteries of theoretical mathematics. (Paul Zeitz, an emeritus math professor at the University of San Francisco, told me that Rusczyk may have been too hasty in reaching this conclusion: performance in math contests, Zeitz said, has little to do with becoming a superb mathematician.) Rusczyk also doubted that he possessed the patience to devote a lifetime to math research. He decided to major in chemical engineering.

And yet he wasn’t quite ready to leave the math-contest world behind. Soon afterward, for fun, Rusczyk, Vandervelde, and Sandor Lehoczky, a younger Olympiad boot camper, created their own mail-in math contest. They called it the Mandelbrot Competition, named after Benoit Mandelbrot, the father of fractals. The trio ran into an issue: they found that the contest problems they came up with were too hard for the participants. Rusczyk discussed the problem with Lehoczky, who was also at Princeton. They concluded that opportunities to learn advanced math were scarce and unevenly distributed. Many young math enthusiasts didn’t know about competitions and élite summer programs; looking back at their Olympiad boot camp experiences, the pair saw that, although some of the mathletes were unquestionably smarter, others simply had earlier exposure to complex math, or access to university mathematicians, or had attended special schools with a high-octane math-team culture. “We should write a book,” Lehoczky declared; it could help democratize advanced math. The two went on to self-publish a two-volume textbook titled “ The Art of Problem Solving .” The book taught “not facts , but approaches ,” they wrote. “If you find yourself memorizing formulas, you are missing the point.”

In the fall of 1993, Rusczyk—newly married to Vanessa—started a Ph.D. in chemical engineering at Stanford. But research still struck him as unappealing. He dropped out after eight weeks. Meanwhile, orders for the math textbook were trickling in. He drove to local schools, hawking the book and hunting for a job as a math teacher. A small private high school hired him, but it wasn’t the right fit, either: he liked teaching, but it was tough to win over the students who abhorred math. Rusczyk figured that he could reach a thousand keen math students a year with the textbook. That summer, he quit the teaching job, too.

In the mid-nineties, Wall Street was emerging as a place where mathematical minds could excel. Rusczyk was recruited for a job at the hedge fund D. E. Shaw; during his interview, he ran into two math-competition geeks he knew. He enjoyed his time trading bonds, but still wanted to build something of his own. After the markets went sideways in 1998, he quit. The following year, he and Vanessa relocated to San Diego, where they bought a fixer-upper; the house was surrounded by national forest and came with three donkeys. For a while, the couple coasted, repairing the house and planting a garden. They became avid hikers. “If I let him choose the hike, it’s always whatever is the highest, whatever is the longest,” Vanessa told me. One of his hobbies was working on old Math Olympiad problems, which could leave him obsessed and cranky until he solved them. The Internet was still new; Rusczyk did some online math tutoring and began thinking about the possibilities.

In 2003, when he was thirty-one, Rusczyk launched artofproblemsolving.com . He used off-the-shelf forum software to set up a community message board and led interactive classes based on his and Lehoczky’s books. Word spread, and young math brainiacs from around the world joined the forum, sharing nerdy puns, posting intriguing problems, and spurring one another along. Yufei Zhao, an early community member from Canada who competed in the I.M.O. three times and is now a math professor at the Massachusetts Institute of Technology, recalled his routine after getting home from high school: “Logging onto this forum was the first thing I did,” he said.

In the twenty years from 1995 to 2014, teams from the U.S. never managed to rank first at the I.M.O. But since 2015 the U.S. has claimed four first-place victories there—an outcome partly attributable to AoPS. Many variables played a role in those successes—including other math enrichment programs and the tutelage of lead coach Po-Shen Loh—but all the members of those winning U.S. teams were AoPS’s students. They were among the first generation to grow up with access to its curriculum. In learning mathematics, just as with studying piano or playing tennis, the earlier that talented individuals start training, the more they may be able to attain. In Rusczyk’s view, this isn’t just a matter of acquiring mathematical knowledge. The pervasive stereotype of children who are labelled as “geniuses” or “gifted” at math assumes that their brilliance requires little effort; by that definition, a genius shouldn’t struggle to learn. (Rusczyk and many other math educators aren’t fans of those labels.) Rusczyk’s boot camp experiences, however, had prepared him for confronting tough, unfamiliar problems of any kind. By normalizing struggle and failure from an earlier age, AoPS was designed to show math prodigies that it was O.K. to stumble and grow.

When COVID-19 struck , AoPS, working pro bono, built a web platform to host the U.S.A. Mathematical Olympiad and other contests. In lieu of the MathCounts national finals, Chandler and her colleagues unofficially offered their 2020 state competition exam on the AoPS site. The day after the test, Rusczyk and David Patrick, a former math professor who is an AoPS curriculum director, reviewed some of the questions in an AoPS chat room before an audience of more than three thousand online students. Rusczyk moderated the chat from two large monitors at his standing desk at work; the walls around him displayed a letter from Benoit Mandelbrot and two delicately rendered oil paintings, by Vanessa, of white manzanita blossoms and red Indian paintbrush. Typing on his keyboard, he walked through the first problem, about an equilateral triangle. Each time he posted a question, a wave of replies came back; he grinned as the students chimed in. “They’re fast, and they all want to be first,” he told me. While discussing a subsequent problem, he laughed at a student’s message: “I got it before you did, Richard!”

While Patrick reviewed the next set of problems, Rusczyk sipped water from a stainless steel mug. I asked whether he had been like these kids.

“Honestly, we’re building stuff for the thirteen-year-old version of ourselves,” he said. “It turns out these kids are a lot like us. They find the same things neat. They find the same things beautiful.”

Many AoPS students learn from one another at the same time as they learn from Rusczyk and his team. Olivia, a precocious twelve-year-old who lives in the rural town of La Grande, Oregon, was able to intuit basic algebra concepts by age eight; last July, she began her first online course with AoPS, in algebra. At the initial weekly class session, the teacher posted the first problem to the chat room, and Olivia, unaccustomed to the text-chat format, copied it down with a pencil. When she glanced back up, other pupils had already submitted their answers. Their speed stunned her. “You could see this panic,” her mother, Angela D’Antonio, recalled. But Olivia soon became a frequent visitor to the online message board to work with other students on hard “challenge problems.” (The other kids were situated in Toronto, India, and Singapore, among other places.) She quickly became one of the first to answer problems during class. Olivia has “just grown by leaps and bounds,” D’Antonio said, and not just in math; on the AoPS boards, Olivia—who is usually shy—has discovered friends with whom she can talk about Dungeons & Dragons and cryptography.

AoPS’s paid resources aren’t cheap. An online high-school-level course with a textbook can cost more than six hundred dollars; the elementary-school-level Beast Academy print books run about a hundred and twenty dollars per set, and a subscription to the accompanying online platform costs ninety-six dollars a year. For much of the past twenty years, U.S. public school systems have mainly focussed on raising the academic proficiency of the weakest students; the families of math overachievers were forced to turn, when they could, to private enrichment programs—from math circles and summer camps to AoPS and newer Web sites, such as Brilliant and Expii. Still, around seventy public school districts, from Albuquerque, New Mexico, to Mankato, Minnesota, now buy AoPS materials for their advanced elementary-school students—a move accelerated by the pandemic.

Meanwhile, since 2011, the nonprofit that Rusczyk founded, the Art of Problem Solving Initiative, has supported a residential summer camp program for mathematically talented middle-school kids from low-income and historically marginalized communities. The camp is now known as Bridge to Enter Advanced Mathematics ( BEAM ) Summer Away, and is held in New York and Los Angeles. Led by a math educator named Daniel Zaharopol, it has provided more than six hundred students with long-term mentoring and support. This year, BEAM is also giving selected fifth-graders at around ten partnering schools across the U.S. free access to AoPS curricula and other supporting resources. In a separate experiment led by AoPS, this fall more than three hundred bright, math-curious pupils from underserved areas of Atlanta, Detroit, San Juan, and elsewhere have been participating in live-streamed AoPS classes for free.

In mathematics, a concept known as the random walk describes a meandering path that is determined, at each step, by a random process, such as tossing a coin. Say you’re standing at a street corner on Fifth Avenue and you flip two coins. If it’s two heads, you walk one block north; if it’s one head and one tail, you walk one block east, and so on. At each intersection, you repeat the process. According to a century-old theorem by a Hungarian mathematician named George Pólya, if you keep up this sort of exercise, after many, many coin flips, the probability of winding up where you started approaches a hundred per cent.

Rusczyk learned about random-walk theory as a teen-ager at a math-tournament lecture; Lehoczky was there, too. Later, while visiting an amusement park, they began flipping coins to decide where to go or what to do. Should they climb over a fence or take the long way around? Have hot dogs or pizza for lunch? The game became a lifelong tradition. Once, coin-flipping their way around Manhattan, the two friends wound up at a Tibetan restaurant; they never would have chosen it, but it turned out to be good.

Our major life choices aren’t purely random, of course, but they can feel like leaps of faith. In some ways, random-walk theory seems like an apt metaphor for Rusczyk’s peregrinations into and away from math. “I got pulled back to the origin,” he said. Creating AoPS was a return to his math-competition roots.

And yet he doesn’t see himself, or his company, as teaching mathematics. Its mission is “to discover, inspire, and train the great problem solvers of the next generation”; its real impact, Rusczyk said, might be “revealing to the kids themselves how much they can do” at something they love. Rusczyk hopes to expand Beast Academy—which is currently used with gifted kids in grades 2-5—into a full K-6 curriculum that public elementary schools can adopt for regular math classes. It would be a further step toward democratizing advanced learning. He figures that some kids are unaware that they are potential math whizzes. He wants to help students “find themselves” earlier than seventh grade, when he found himself. He hopes that the curriculum might help guide more young brainiacs toward lives in math, or outside of it—in science, finance, or Silicon Valley.

One Sunday, I Zoomed with Rusczyk while he and Vanessa worked a morning shift in the AoPS warehouse. They’d woken up early and sipped coffee in their garden as dawn broke, then unloaded hay to feed their donkeys. Rusczyk had driven his dark gray Tesla to the AoPS office, where he’d done a quick sanitizing wipe-down of surfaces in the second-floor break room and bathrooms. He printed out book-order invoices in the finance office, then ran down to unlock the front door for Vanessa, who had driven separately. A petite brunette with frizzy tresses, she walked in wearing flip-flops, shorts, and an olive-green tank top; Rusczyk, who was dressed in green cargo shorts and a red T-shirt, looked serious and a bit tired. His days were crammed with e-mails and video and phone meetings—the workaday business of shepherding his expanding firm in the middle of a pandemic.

In the shipping room, he grabbed Beast Academy books, which were stocked on metal shelves, and laid them atop a growing tower of crisscrossed book orders on a red plastic cart. Each time the cart filled up, he transferred the books to an array of tables. It was work he actually enjoyed, he told me. The textbooks were a direct link to the enthusiastic math learners who would soon be engrossed in their pages.

“Feels like we’re doing something real,” Vanessa said, working at her own book cart.

“Yeah—doing something real,” Rusczyk said. A couple thousand books would be boxed and shipped the next day.

More Science and Technology

• What happens when patients find out how good their doctors really are ?
• Life in Silicon Valley during the dawn of the unicorns ?
• The end of food .
• The histories hidden in the periodic table .
• The detectives who never forget a face .
• What is the legacy of Laika, the first animal launched into orbit ?
• Sign up for our daily newsletter to receive the best stories from The New Yorker .

By signing up, you agree to our User Agreement and Privacy Policy & Cookie Statement . This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

By Louisa Thomas

By H. C. Wilentz

By Dan Greene

Calcworkshop

Least Common Multiple Simple How-To w/ 9+ Examples!

// Last Updated: November 6, 2020 - Watch Video //

Did you know that the least common multiple, or LCM, is the smallest positive multiple that is common to two or more numbers?

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)

But first, what is a multiple, and how is it different than a factor?

Let’s look at an example.

List the multiples and factors of 6.

• Multiples of 6 : 6, 12, 18, 24, 30, 36, 42, …
• Factors of 6 : 1, 2, 3, and 6

So, factors are the integers we multiply together to get the original number.

And multiples are all the integers that 6 can go into.

That means, whenever you see the word “multiple” you want to think multiply!

How do we find the least common multiple?

Well, just like we saw with finding the greatest common factor , there are actually two techniques for identifying the LCM:

• Prime Factorization

Using our listing method , we will work L-C-M backward:

• M : List multiples for each number
• C : Identify common multiples
• L : Choose the lowest multiple (smallest number they have in common)

And for the prime factorization method , we will create a factor tree and identify each number’s prime factors. Then we will select all factors, always choosing the largest common factor.

List Method

The listing method, sometimes called the roster method, is simply a listing of multiples. When we learned to multiply we employed a technique called skip counting to help us recognize equal groups, and that’s basically what we are doing here — we’re going to skip count by each integer given.

For example, let’s find the least common multiple of 6 and 10 using both techniques.

First, we will use the listing method by “skip counting” and select the lowest integer they both have in common.

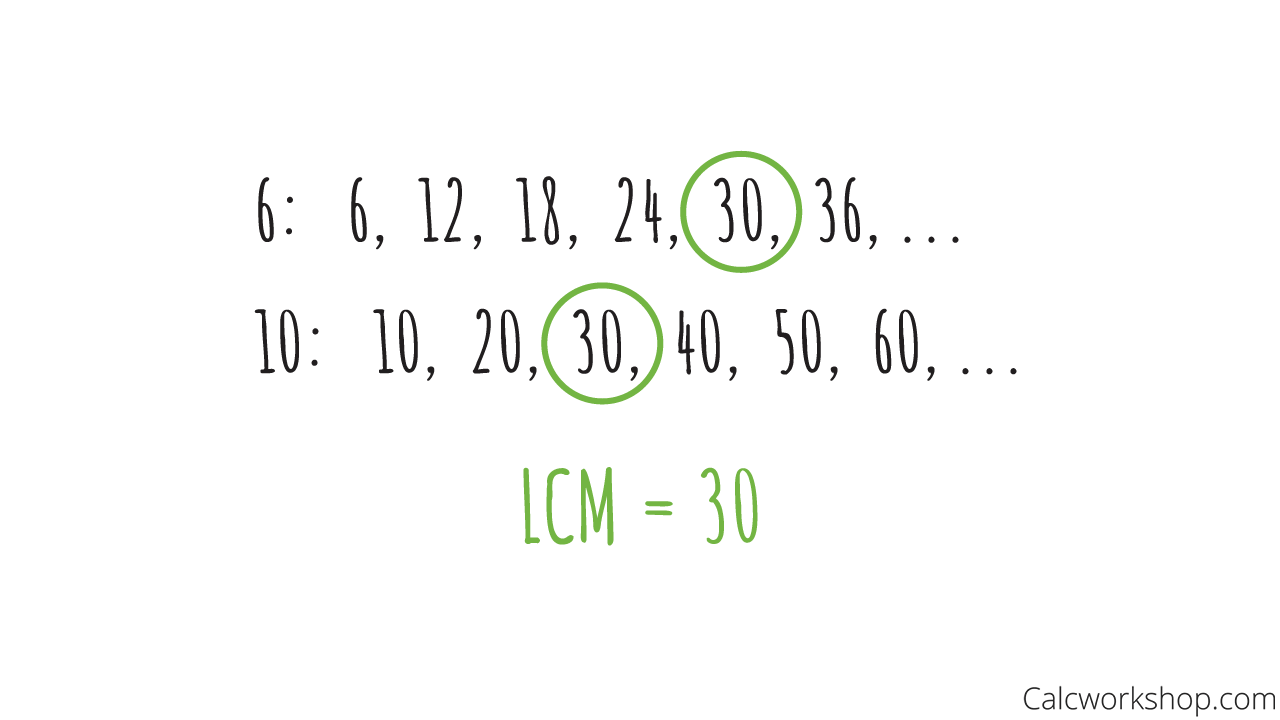
Find The LCM of the Numbers Using Lists of Multiples

Prime Factorization Method

Now, let’s see how to use the prime factorization method. For this technique, we create factor trees for each integer as seen below, and then multiply the largest of all prime values found in both trees.

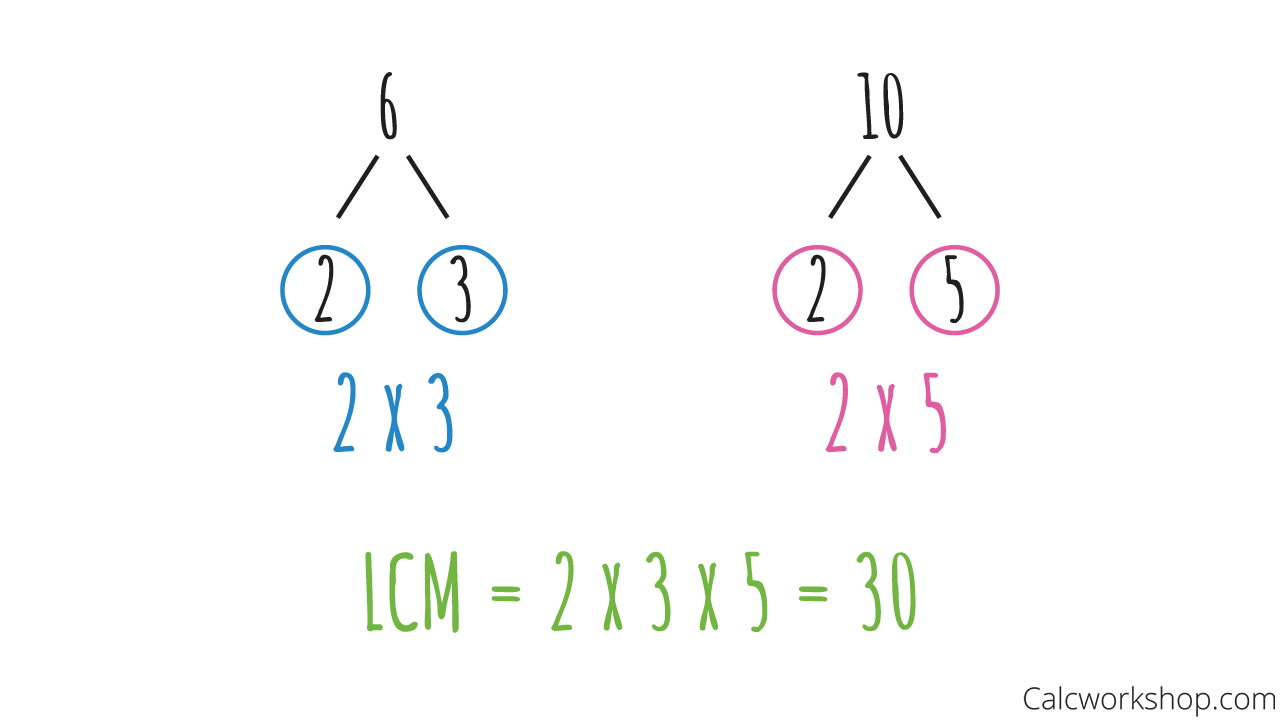
Prime Factorization of 2 Numbers

Method Summary

Here’s a breakdown of the two methods for identifying the Least Common Multiple:

• When we list factors, we choose the LOWEST common number.
• When we use prime factorization, we choose MORE – most power from each factor.

As you have probably noticed, the first method is easier to use, as all we’re doing is multiplying (i.e., skip-counting) and selecting the lowest number.

But this method is not very practical for integers bigger than 12, whereas the prime factorization method is tried and true and will work for any integer as noted on the Art of Problem Solving .

Example — Hard LCM Problem

Let’s look at another example, where using prime factorization really shows itself to be the best method for discovering the least common multiple

Find the LCM of 8 and 42.

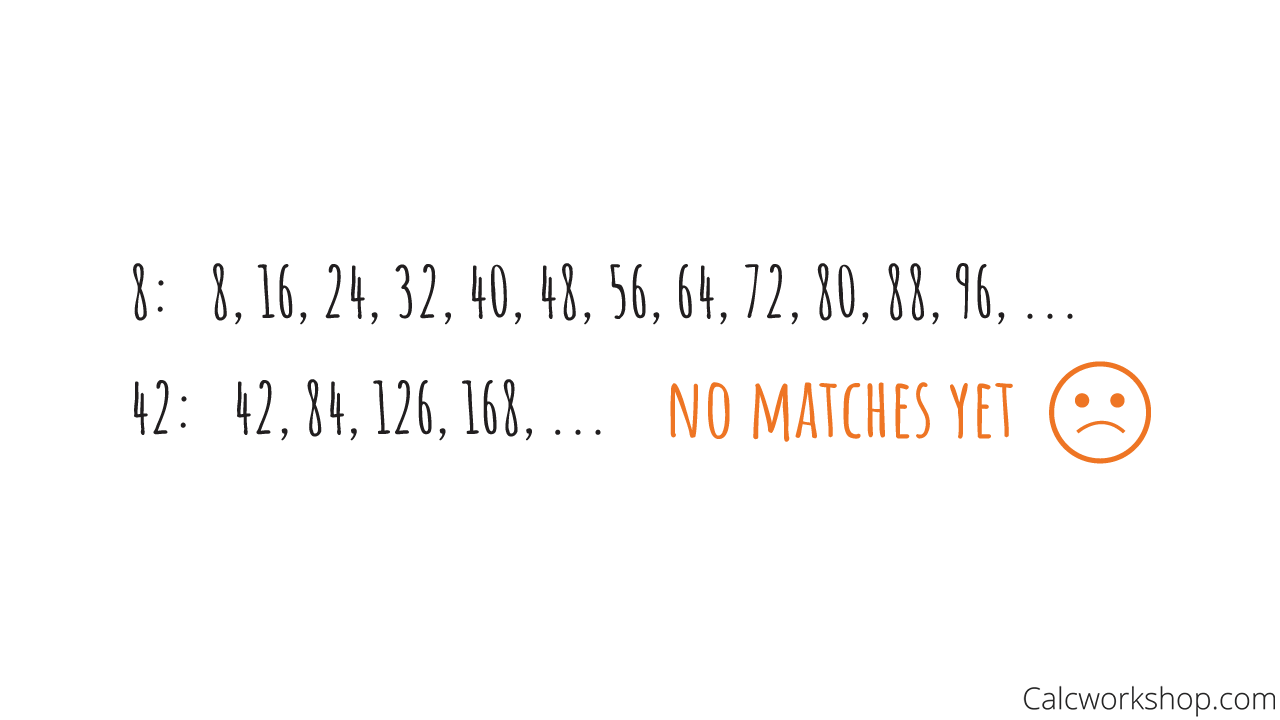
LCM of 42 and 8 — Example

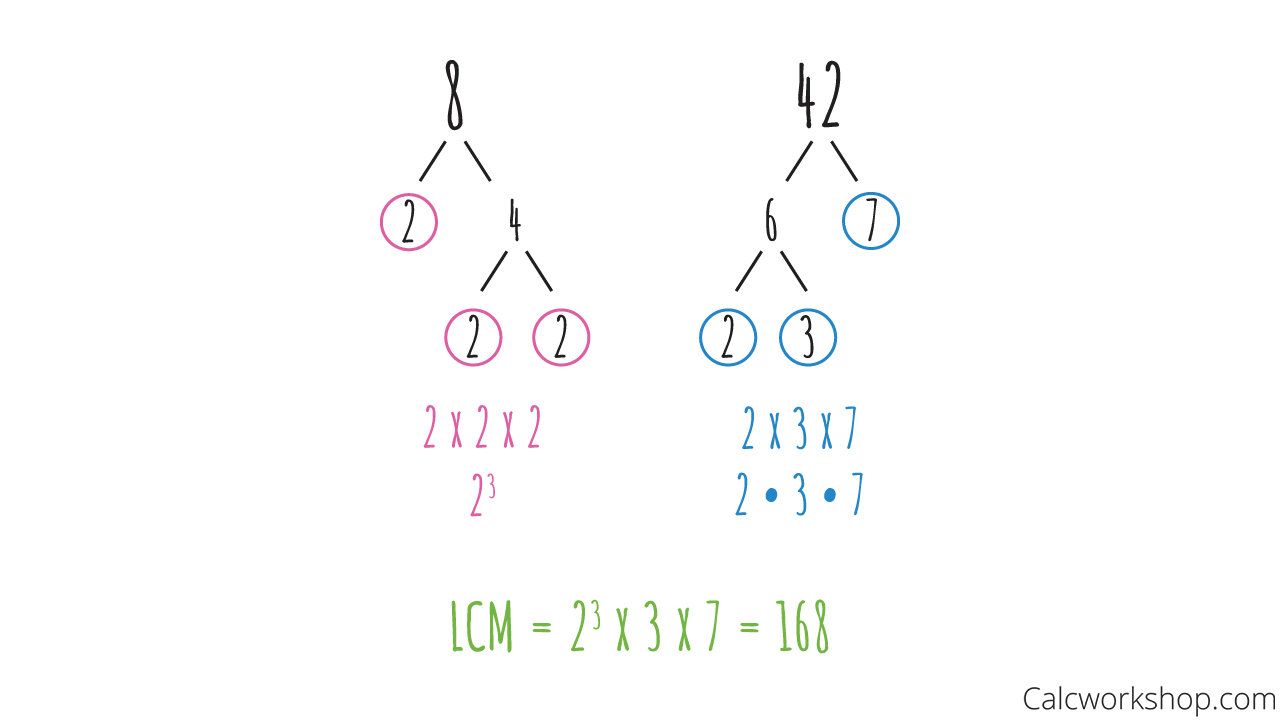
LCM Using Prime Factorization

As you can see, prime factorization helped us to locate the LCM much faster than skip-counting.

Example — LCM Of Three Numbers

What about finding the LCM for three numbers?

Like we saw with the example above, the method we should employ when discovering the least common multiple for three numbers is prime factorization.

For example, let’s find the LCM of 90, 120, and 300

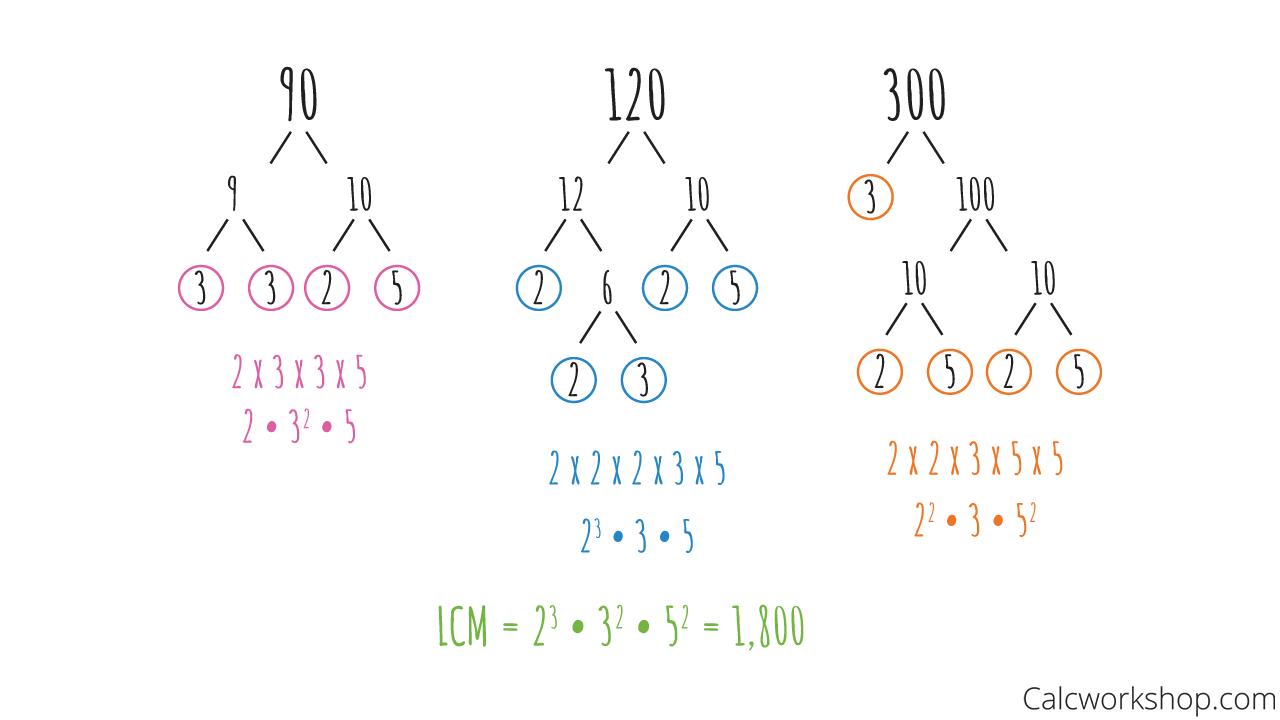
How To Find LCM of 3 Numbers Using Prime Factorization

Trying to list multiples for these three numbers would have been incredibly tedious. Aren’t you glad we just used prime factorization!

Worksheet (PDF) — Hands on Practice

It’s all fun and games until you try it on your own. So give these worksheets a go — and improve your knowledge!

Least Common Multiple — Practice Problems Least Common Multiple — Step-by-Step Solutions

Video Tutorial — Full Lesson w/ Detailed Examples

Together we will look at various examples of finding the least common multiple and ensuring that we can employ both methods (listing and prime factorization) with success.

• Introduction to Video: Least Common Multiple
• 00:00:29 – How do you find the LCM?
• 00:08:02 – Determine the LCM using both methods (Examples #1-2)
• 00:13:02 – Find the least common multiple for two or three numbers (Examples #3-8)
• 00:30:03 – Uncover the LCM for three numbers using prime factorization (Examples #9-10)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.

LEAST COMMON MULTIPLE

Calculating the least common multiple is something many Mathletes are asked to do, but in this plan they will use their understanding of the least common multiple to stretch themselves to solve more complex problems.

Download the Mathlete handout.

Download the coaches version with solutions.

Reset password New user? Sign up

Existing user? Log in

Greatest Common Divisor / Lowest Common Multiple

Concept quizzes.

• GCD / LCM Warmup
• Greatest Common Divisor
• Lowest Common Multiple
• Relationship between GCD and LCM
• GCD and LCM - Problem solving
• Euclidean Algorithm

Challenge Quizzes

• Greatest Common Divisor / Lowest Common Multiple: Level 1 Challenges
• Greatest Common Divisor / Lowest Common Multiple: Level 2 Challenges
• Greatest Common Divisor / Lowest Common Multiple: Level 3 Challenges
• Greatest Common Divisor / Lowest Common Multiple: Level 4 Challenges
• Greatest Common Divisor / Lowest Common Multiple: Level 5 Challenges

Greatest common divisors and least common multiples can be applied in more practical scenarios than you might expect: from buying sandwich ingredients efficiently to being able to create complex musical patterns by overlaying many different rhythms.

Expect to see and learn how to solve questions like this one:

Once you’ve mastered the techniques for studying the factors and multiples of numbers, a natural next step is to consider comparing two numbers by these measures: given any two numbers, what divisors do they share and what multiples do they share? The computation of the greatest common divisor and least common multiple are only the beginning; from there it’s possible to reach towards many more advanced proofs, techniques, and practical applications!

• Division Algorithm
• Bezout's Identity
• Extended Euclidean Algorithm

Problem Loading...

Note Loading...

Set Loading...

Prealgebra is a term commonly used to refer to the level of mathematics a student studies before moving on to algebra and/or geometry . Prealgebra is difficult to define precisely other than "the math taken before algebra" because of the broad number of subjects that various prealgebra curriculums use.

A typical prealgebra curriculum more-or-less consists of:

• Arithmetic with the natural numbers and integers .
• An introduction to fractions and decimals .
• An introduction to the basics of number theory ( prime factorization , multiples , least common multiple , greatest common divisor , etc.)
• An introduction to the basics of statistics .
• Exponents , the root operation , and scientific notation .
• Solving linear equations , inequalities , and modeling word problems using variables.
• Ratios , computing simple conversions and rates .
• Percentages .
• An introduction to geometry (computing area, perimeter, angles, etc.).
• the Art of Problem Solving: Prealgebra by David Patrick (Details) .

AoPS Classes

The AoPS classes for prealgebra are a good starting point for those who finished up Beast Academy 's curriculum or have a working understanding of simple arithmetic. Note that AoPS's classes are quite challenging as each class is considerably more in-depth and problem-solving-oriented compared to the equivalent typical school course in prealgebra which focuses more on rote memorization.

• Prealgebra 1
• Prealgebra 2
• Introductory Mathematics Topics

Something appears to not have loaded correctly.

Click to refresh .

• Edit source
• View history

Alcumus is a game that is designed to help students focus on a variety of subjects, prealgebra, algebra, number theory, counting and probability, geometry, and precalculus.

Alcumus is free; however, you must have an AoPS account to play. For instructions on how to get one, visit the page Creating An Account . Users are able to earn achievements for their accounts. They are also able to receive quests, and complete them.

There are six sections on Alcumus, along with many topics. Here they are!

• 1.1 Pre-Algebra
• 1.2 Algebra
• 1.3 Number Theory
• 1.4 Counting & Probability
• 1.5 Geometry

Pre-Algebra [ ]

• Arithmetic - Addition
• Arithmetic - Multiplication
• Arithmetic - Negatives
• Arithmetic - Subtraction
• Arithmetic - Reciprocals
• Arithmetic - Division
• General Positive Exponents
• Order of Operations
• Negative and Zero Exponents
• Divisibility
• Primes and Composite Basics
• Prime Factorization
• Least Common Multiple
• Greatest Common Divisor
• Fraction Multiplication
• Fraction Division
• Fractions And Exponents
• Simplifying Fractions
• Fraction Addition And Subtraction
• Mixed Numbers
• Expressions
• Basic Linear Equations
• Advanced Linear Equations
• Word Problems
• Inequalities
• Decimal Arithmetic
• Rounding Decimals
• Decimals and Fractions
• Repeating Decimals
• Ratio Basics
• Proportions
• Unit Conversions
• Speed and Other Rates
• Simple Percents
• Combining Percents
• Integer Square Roots
• Non-integer Square Roots
• Angle Basics
• Parallel Lines and Triangles
• Angles In a Polygon
• Length and Perimeter
• The Pythagorean Theorem
• Special Right Triangles
• Quadrilaterals
• Basic Statistics
• Statistics - Reading Tables or Charts
• Counting Lists
• Venn Diagrams
• The Multiplication Principle in Counting
• Permutations
• Casework Counting
• Counting Pairs
• Basic Probability
• All Topics in Prealgebra

Algebra [ ]

• Prerequisites - Arithmetic Review
• Prerequisites - Exponent Laws
• Prerequisites - Square Roots
• Prerequisites - Fractional Exponents
• Evaluating Expressions
• Simplifying One-Variable Expressions
• One-Variable Distribution
• One-Variable Linear Equations
• Word Problems in One Variable
• Linear Equations in Disguise
• Solving Two-Variable Systems
• Two-Variable Word Problems
• Advanced Systems
• Advanced Systems of Equations
• Direct Proportion
• Inverse Proportion
• Rate Problems
• Distance in the Plane
• Midpoint of a Segment
• Graphing Lines
• Graphing Multiple Lines
• Solving Linear Inequalities
• Multiplying Binomials
• Factoring Monic Quadratics
• Factoring General Quadratics
• Sum and Products of Roots
• Square of a Binomial
• Difference-of-Squares
• Rationalizing Denominators
• Simon's Favorite Factoring Trick
• Complex Number Arithmetic
• Quadratic Formula/Discriminant
• Completing the Square
• Quadratic Optimization
• Complex Quadratics
• Graphing Quadratics
• Graphing Circles
• Quadratic Inequalities
• Evaluating Functions
• Domain and Range
• Function Composition
• Inverse Functions
• Functional Operations
• Graphing Functions
• Polynomial Basics
• Polynomial Multiplication
• Exponential and Logarithm Basics
• Interest Rates
• Logarithm Basics
• Radical Expressions and Functions
• Absolute Value
• Floor and Ceiling
• Rational Expressions of Polynomials
• Piecewise-Defined Functions
• Arithmetic Sequences
• Arithmetic Series
• Geometric Sequences
• Geometric Series
• Clever Algebraic Manipulations
• All Topics in Algebra

Number Theory [ ]

• Primes and Composites Basics
• This is sometimes known as Greatest Common Factor as well.
• The Euclidean Algorithm
• LCM/GCD Problem Solving
• Counting Divisors
• Divisor Arithmetic
• Converting from Base 10
• Converting to Base 10
• Base Number Problem-Solving
• Base Number Arithmetic
• The Last Digit (Base 10)
• Terminating Decimals
• Congruence and Residues
• Modular Arithmetic Sums
• Modular Arithmetic
• Patterns in Modular Arithmetic
• Divisibility Rules
• Divisibility Problem-Solving
• Modular Arithmetic Inverses
• Modular Arithmetic Congruences
• Modular Arithmetic Systems
• Perfect Powers
• All Topics in Number Theory

Counting & Probability [ ]

• Counting Numbers in Lists
• Counting Independent Events
• Complementary Counting
• Constructive Counting
• Counting with Restrictions
• Counting with Systems
• Correcting for Overcounting with Division
• Basic Combinations
• Computing Combinations
• Combinations with Restrictions
• Distinguishability
• Basic Probability as Counting
• Basic Probability with Combinations
• Probability with Casework
• Complementary Probability
• Binomial Probability
• Multiplying Probabilities
• Advanced Probability with Combinations
• Probability - Think About It!
• Using Geometry in Probability
• Expected Value
• Pascal's Triangle
• Binomial Theorem
• All Topics in Counting & Probability

Geometry [ ]

• 1 Swapnil Garg
• 3 2015 MATHCOUNTS National Competition