what is the mean absolute deviation of sherwin's homework scores

• Calculators
• Conversions

Statistics Calculator: Mean Absolute Deviation (MAD)

Use this calculator to compute the mean absolute deviation from a data set.

Mean Absolute Deviation Calculator

Instructions.

This calculator computes the mean absolute deviation from a data set:

You do not need to specify whether the data is for an entire population or from a sample. Just type or paste all observed values in the box above. Values must be numeric and may be separated by commas, spaces or new-line. Press the "Submit Data" button to perform the computation. To clear the calculator, press "Reset".

What is the mean absolute deviation

The mean deviation is a measure of dispersion , A measure of by how much the values in the data set are likely to differ from their mean. The absolute value is used to avoid deviations with opposite signs cancelling each other out.

Mean absolute deviation formula

Mean Absolute Deviation Calculator

What is mean absolute deviation mean absolute deviation calculator, how to find mean absolute deviation (mad) mean absolute deviation formula, how to find mad - an example.

The mean absolute deviation calculator is a tool that can help you quickly find the mean absolute deviation around the mean, median, or any other number. If you want to know what is mean absolute deviation - we break down the name in the article below. We also explain how to find it using a mean absolute deviation formula, or by following a few simple steps.

Now, input up to 50 numbers and get the mean absolute deviation for your dataset!

The mean absolute deviation shows us how spread out the numbers are in a data set. But how? And what does deviation even mean?

• Deviation is the difference from what is usual .
• An absolute number takes the positive value of a number, without regards to its sign.
• Mean is an average of a set of numbers.

So, what is the mean absolute deviation? It's the average of every value's distance from a certain central point . This point can be a mean, median, mode , or any other statistically significant number.

To calculate it, use our mean absolute deviation calculator or do it on your own using the How to find mean absolute deviation? section below. How to use the MAD calculator? Select the central point. If you want it to be mean or median of your data set - the calculator will calculate it for you. If not, choose the option other and input an appropriate value. All that's left for you to do is input your data set and get your result!

If you are wondering how to find MAD, our calculator uses the mean absolute deviation formula:

M A D = 1 n ∑ i = 1 n ∣ x i − m ∣ \small MAD = \frac{1}{n}\sum_{i=1}^n|x_i-m| M A D = n 1 ​ ∑ i = 1 n ​ ∣ x i ​ − m ∣ ,

• n is the amount of numbers in the set;
• x i is the i th number of the set; and
• m is a certain central point (mean, median, mode, etc)

So, to find mean absolute deviation, follow these steps:

Determine the central point: m \footnotesize m m .

Find the difference from the central point for each point: x i − m \footnotesize x_i - m x i ​ − m .

Calculate the absolute value of each difference: ∣ x i − m ∣ \footnotesize |x_i - m| ∣ x i ​ − m ∣ .

Find the mean of the absolute deviations - sum up all the absolute differences and divide them by the amount of data points: 1 n ∑ ∣ x i − m ∣ \footnotesize\frac{1}{n}\sum|x_i-m| n 1 ​ ∑ ∣ x i ​ − m ∣ .

Now, let's go to an example to see how to find the mean absolute deviation by using these steps.

Let's calculate the mean absolute deviation for 6 friends' lost socks in the last year: 3, 17, 9, 7, 13, 11.

• Let's say you want to calculate the MAD around the mean. In this case, the mean is the amount of socks lost, on average, by one person:

m = (3 + 17 + 9 + 7 + 13 + 11) / 6 = 60 / 6 = 10

• Calculate the deviation from the mean:
• 3 - 10 = -7
• 17 - 10 = 7
• 9 - 10 = -1
• 7 - 10 - -3
• 13 - 10 = 3
• 11 - 10 = 1
• Find the absolute value of each deviation:
• Find the mean of absolute values of each deviation:

MAD = (7 + 7 + 1 + 3 + 3 + 1) / 6 = 3.67

It means that, on average, the amount of lost socks differs from the mean by 3.67 "socks". What does it mean? It means that, in theory, each of 6 friends lost ten socks in the last year on average, while in reality this isn't the case - they lost anywhere between 6.33 and 13.67 socks (10±3.67).

Even if you now know how to find MAD by hand, you don't need to repeat these tedious calculation anymore. Just use our mean absolute deviation calculator!

• MAD can indicate mean absolute deviation or median absolute deviation . These are not the same. In the median absolute deviation , you calculate the median of the distances from a central point.
• The distribution of data points can be also portrayed with standard deviation. Although similar in concept, standard deviation gives us the opportunity to further analyze a dataset with variance , estimate sample size , and so on.

Now you know what is mean absolute deviation and how to calculate it. Before you go, check out our other descriptive statistics calculators like this percentile calculator !

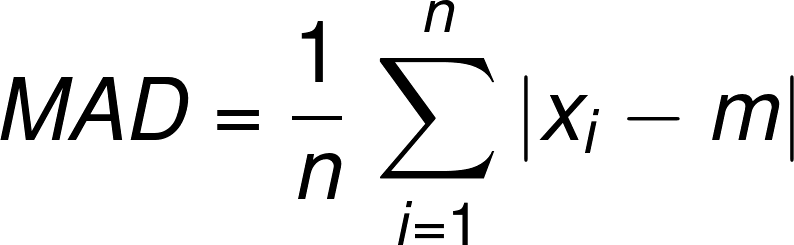
Beta distribution

Circumference, least to greatest decimals.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (182)
• Other (182)
• Discover Omni (40)

If you could change one thing about college, what would it be?

Graduate faster

Better quality online classes

Flexible schedule

Access to top-rated instructors

Mean Absolute Deviation (MAD) - Meaning & Formula

12.08.2021 • 5 min read

Sarah Thomas

Subject Matter Expert

Measuring mean absolute deviation is an easy way to understand the degree of variation across statistical data points. In this article, we’ll define mean absolute deviation; discuss how it differs from its more common counterpart, standard deviation; and show how to calculate it in four quick steps.

What Is Mean Absolute Deviation?

Some easy mad examples, why use mad and not standard deviation, key terms to know, 4 steps on how to find mad, don't overpay for college statistics.

Take Intro to Statistics Online with Outlier.org

From the co-founder of MasterClass, earn transferable college credits from the University of Pittsburgh (a top 50 global school). The world's best online college courses for 50% less than a traditional college.

What is MAD in math? In math and statistics , MAD stands for mean absolute deviation.

Mean absolute deviation (MAD) is a measure of the average absolute distance between each data value and the mean of a data set. Similar to standard deviation , MAD is a parameter or statistic that measures the spread, or variation, in your data.

Mean Absolute Deviation Definition - A measure of the average absolute distance between your data points and the mean of your data set. To calculate MAD, we measure the absolute distance (or absolute deviation) between each data point and the mean. We then take the average of those distances. This average distance is what we call the mean absolute deviation.

The Mean Absolute Deviation formula is then:

Σ \Sigma Σ is known as Sigma and means to sum up

| | are vertical bars that mean absolute value

x i x_i x i ​ is each value such as 4 and 9

x̄ is the mean

n is the total number of data points in your data set

Let’s look at two quick examples. Below are two sets of data. What is the mean absolute deviation in each case?

Before we calculate MAD, notice that the mean, or average, of both data sets is 5. In Data Set A, however, the data is more closely clustered around the mean. This tells us that MAD must be smaller for Data Set A than it is for Data Set B since the distances between the data values and the mean are smaller. We can see this more clearly by plotting our data onto dot plots.

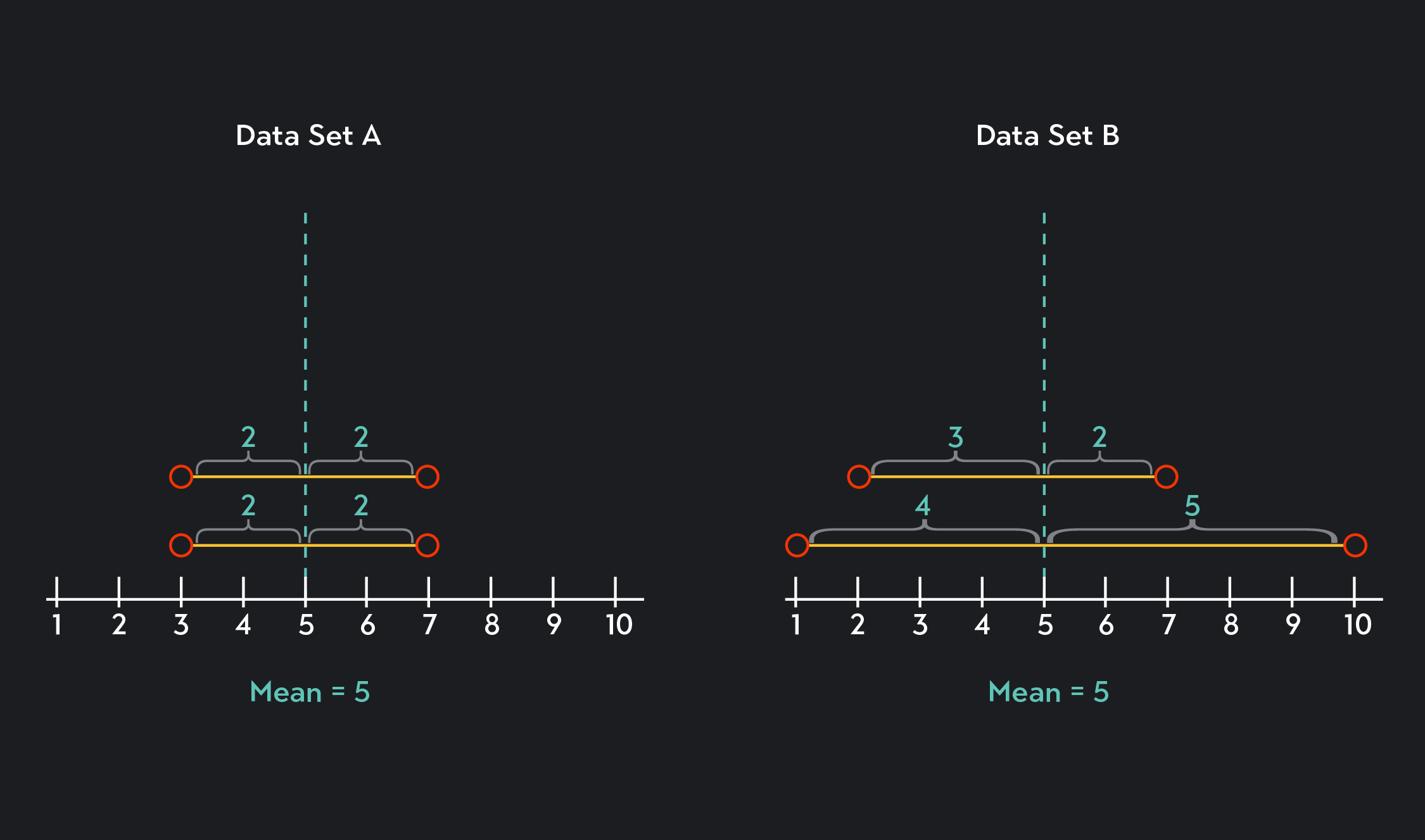
Using these dot plots, we can visualize the deviations.

For Data Set A, we see that every single data point deviates from the mean by 2. Calculating MAD in this case is easy; the average of four twos is just two!

For Data Set B, we see that the data is more varied. The absolute deviations are 4, 3, 2, 5. The average of these absolute deviations is 3.5.

Concretely, what do these figures tell us? In the first instance, MAD tells us that, on average, the values in Data Set A deviate from the mean by 2.

In the second case, MAD tells us that, on average, the values in Data Set B deviate from the mean by 3.5.

As we mentioned earlier, MAD and standard deviation are both measures of spread — they tell you how much variation there is in your data relative to the mean. So what then is the difference between MAD and standard deviation, and why would you want to use one of these measures over the other?

While MAD measures the average absolute deviation, standard deviation takes the square root of the average squared deviations.

At this point, you may be wondering why we bother taking absolute values or squares of the deviations. Good question! Whenever you measure deviations from a mean, you run into the problem of dealing with positive and negative values.

Some data points lie above the mean, while others lie below it, so if you measure the deviations as each data value minus the mean ( ∣ x i − x ˉ ∣ \left | x_i-\bar{x} \right | ∣ x i ​ − x ˉ ∣ ), you’ll end up with positive deviations for values that are greater than the mean and negative deviations for values that are less than the mean. The negative deviations partially or wholly cancel out the positive deviations, and this interferes with the goal of calculating the average deviation.

MAD and standard deviations deal with the problem of having positive and negative deviations in different ways. When you calculate MAD, you take the absolute value of the deviations, which turns all the deviations positive. When you calculate standard deviation, you square all the deviations, which turns the deviations positive but changes the units of the deviations into squared units. As an added step, when calculating standard deviation, you take the square root of the average square deviations to get the units back into their original form.

Although standard deviation seems like the clunkier of the two measurements, it’s actually the more common one. Because calculating standard deviation involves squared deviations, it’s more sensitive to values that are farther away from the mean. You can think of standard deviation as a weighted average that gives less weight to the values that lie close to the mean and more weight to the data points that lie farther away from the mean. For this reason, standard deviation tends to be larger than MAD.

To understand mean absolute deviation, you also need to know the following terms:

Mean : The average of a data set. To find the mean, add up all the values in your data and divide by the total number of data points.

Absolute Value : Absolute value, denoted by two parallel lines | |, is the non-negative value of a real number, x. If x is positive, the absolute value is positive. If x is negative, the absolute value is positive. For example, |5| = 5 and |-3.4| = 3.4. If you have an operation within the absolute value, complete the operation before taking the absolute value. So... |3-5|=|-2|=2. The absolute value essentially removes negative signs from whatever lies within the symbol!

Deviation : The word deviation shows a departure from a standard or a norm. When we calculate deviations in statistics, we’re typically finding the distance between a given value and some norm, such as the mean. As an example, say the average temperature of sodas in a vending machine is 38 degrees Fahrenheit. You buy a soda from the vending machine and it is 39.5 degrees. The deviation between the temperature of your soda and the average temperature of sodas in the vending machine is 1.5 degrees!

Summation : Summation is the process of adding elements together. Taking an average, or mean, involves a summation: you add up all of the elements in the data before dividing by the total number of elements in the data set. In math and statistics, summation is symbolized by the capital Greek letter sigma 𝝨.

Assume you have the following data.

-2, 1, 5, 8

To calculate mean absolute deviation without the use of a dot plot, follow these easy steps. Recall that the MAD formula is:

1. Calculate the mean of the data, x ˉ \bar{x} x ˉ

2. Find the absolute deviation between each data point and the mean, ∣ x i − x ˉ ∣ \left | x_i-\bar{x} \right | ∣ x i ​ − x ˉ ∣

3. Take the summation of the distances you found in Step 2, ∑ ∣ x i − x ˉ ∣ \sum \left | x_i-\bar{x} \right | ∑ ∣ x i ​ − x ˉ ∣

4. Take the average deviation by dividing the sum found in Step 3 by the total number of data points, n. ∑ ∣ x i − x ˉ ∣ n \frac{\sum \left | x_i-\bar{x} \right |}{n} n ∑ ∣ x i ​ − x ˉ ∣ ​

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Intro to Statistics

How data describes our world.

Precalculus

Master the building blocks of Calculus.

The mathematics of change.

Intro to Microeconomics

Why small choices have big impact.

How To Make a Box Plot

The ability to clearly visualize data is critical to getting the most out of your statistical analysis. In this article, you’ll learn step-by-step how to construct a box plot, one of the simplest and most efficient tools for conveying information regarding a data set.

Understanding Sampling Distributions: What Are They and How Do They Work?

Sampling distribution is a key tool in the process of drawing inferences from statistical data sets. Here, we'll take you through how sampling distributions work and explore some common types.

Concave Up and Concave Down: Meaning and Examples

In this article, we’ll learn the definition of concavity. Using graphs, we’ll compare concave up vs. concave down curves. Then, we’ll discuss how to find points of inflection and identify intervals of concave up and concave down, using examples.

Rachel McLean

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

43.3: Variability and MAD

• Last updated
• Save as PDF
• Page ID 40876

Let's study distances between data points and the mean and see what they tell us.

Exercise \(\PageIndex{1}\): Shooting Hoops (Part 1)

Elena, Jada, and Lin enjoy playing basketball during recess. Lately, they have been practicing free throws. They record the number of baskets they make out of 10 attempts. Here are their data sets for 12 school days.

\(4\qquad 5\qquad 1\qquad 6\qquad 9\qquad 7\qquad 2\qquad 8\qquad 3\qquad 3\qquad 5\qquad 7\)

\(2\qquad 4\qquad 5\qquad 4\qquad 6\qquad 6\qquad 4\qquad 7\qquad 3\qquad 4\qquad 8\qquad 7\)

\(3\qquad 6\qquad 6\qquad 4\qquad 5\qquad 5\qquad 3\qquad 5\qquad 4\qquad 6\qquad 6\qquad 7\)

• Calculate the mean number of baskets each player made, and compare the means. What do you notice?
• What do the means tell us in this context?

Exercise \(\PageIndex{2}\): Shooting Hoops (Part 2)

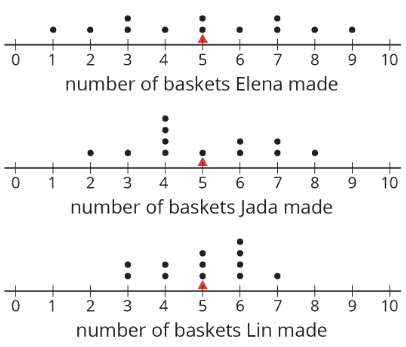
Here are the dot plots showing the number of baskets Elena, Jada, and Lin each made over 12 school days.

• On each dot plot, mark the location of the mean with a triangle (\(\Delta\)). Then, contrast the dot plot distributions. Write 2–3 sentences to describe the shape and spread of each distribution.

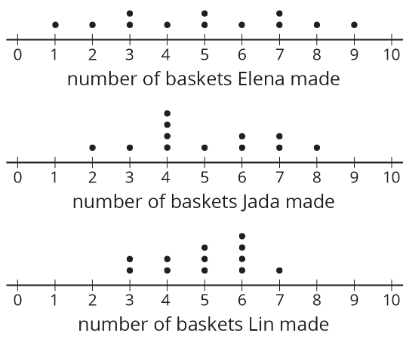
• Would you say that all three students play equally well?
• Would you say that all three students play equally consistently?
• If you could choose one player to be on your basketball team based on their records, who would you choose?

Exercise \(\PageIndex{3}\): Shooting Hoops (Part 3)

The tables show Elena, Jada, and Lin’s basketball data from an earlier activity. Recall that the mean of Elena’s data, as well as that of Jada and Lin’s data, was 5.

• Record the distance between each of Elena’s scores and the mean.

Now find the average of the distances in the table. Show your reasoning and round your answer to the nearest tenth.

This value is the mean absolute deviation (MAD) of Elena’s data.

Elena’s MAD: ________

• Find the mean absolute deviation of Jada’s data. Round it to the nearest tenth.

Jada’s MAD: _________

• Find the mean absolute deviation of Lin’s data. Round it to the nearest tenth.

Lin’s MAD: _________

• Compare the MADs and dot plots of the three students’ data. Do you see a relationship between each student’s MAD and the distribution on her dot plot? Explain your reasoning.

Are you ready for more?

Invent another data set that also has a mean of 5 but has a MAD greater than 2. Remember, the values in the data set must be whole numbers from 0 to 10.

Exercise \(\PageIndex{4}\): Game of 22

Your teacher will give your group a deck of cards. Shuffle the cards, and put the deck face down on the playing surface.

• To play: Draw 3 cards and add up the values. An ace is a 1. A jack, queen, and king are each worth 10. Cards 2–10 are each worth their face value. If your sum is anything other than 22 (either above or below 22), say: “My sum deviated from 22 by ____ , ” or “My sum was off from 22 by ____ .”
• To keep score: Record each sum and each distance from 22 in the table. After five rounds, calculate the average of the distances. The player with the lowest average distance from 22 wins the game.

Average distance from 22: ____________

Whose average distance from 22 is the smallest? Who won the game?

We use the mean of a data set as a measure of center of its distribution, but two data sets with the same mean could have very different distributions.

This dot plot shows the weights, in grams, of 22 cookies.

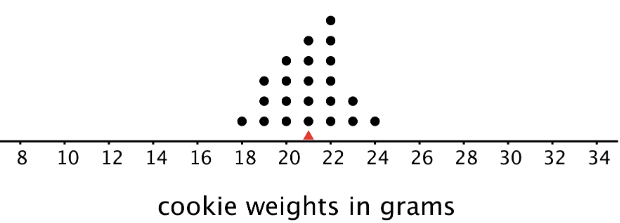
The mean weight is 21 grams. All the weights are within 3 grams of the mean, and most of them are even closer. These cookies are all fairly close in weight.

This dot plot shows the weights, in grams, of a different set of 30 cookies.

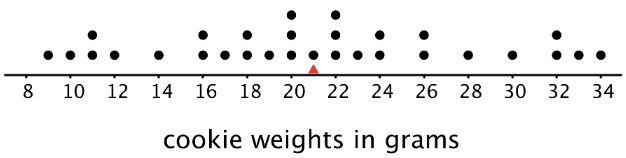
The mean weight for this set of cookies is also 21 grams, but some cookies are half that weight and others are one-and-a-half times that weight. There is a lot more variability in the weight.

There is a number we can use to describe how far away, or how spread out, data points generally are from the mean. This measure of spread is called the mean absolute deviation (MAD) .

Here the MAD tells us how far cookie weights typically are from 21 grams. To find the MAD, we find the distance between each data value and the mean, and then calculate the mean of those distances.

For instance, the point that represents 18 grams is 3 units away from the mean of 21 grams. We can find the distance between each point and the mean of 21 grams and organize the distances into a table, as shown.

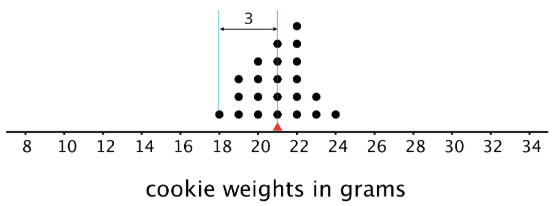
The values in the first row of the table are the cookie weights for the first set of cookies. Their mean, 21 grams, is the mean of the cookie weights .

The values in the second row of the table are the distances between the values in the first row and 21. The mean of these distances is the MAD of the cookie weights .

What can we learn from the averages of these distances once they are calculated?

• In the first set of cookies, the distances are all between 0 and 3. The MAD is 1.2 grams, which tells us that the cookie weights are typically within 1.2 grams of 21 grams. We could say that a typical cookie weighs between 19.8 and 22.2 grams.
• In the second set of cookies, the distances are all between 0 and 13. The MAD is 5.6 grams, which tells us that the cookie weights are typically within 5.6 grams of 21 grams. We could say a typical cookie weighs between 15.4 and 26.6 grams.

The MAD is also called a measure of the variability of the distribution. In these examples, it is easy to see that a higher MAD suggests a distribution that is more spread out, showing more variability.

Glossary Entries

Definition: Average

The average is another name for the mean of a data set.

For the data set 3, 5, 6, 8, 11, 12, the average is 7.5.

\(3+5+6+8+11+12=45\)

\(45\div 6=7.5\)

Definition: Mean

The mean is one way to measure the center of a data set. We can think of it as a balance point. For example, for the data set 7, 9, 12, 13, 14, the mean is 11.

To find the mean, add up all the numbers in the data set. Then, divide by how many numbers there are. \(7+9+12+13+14=55\) and \(55\div 5=11\).

Definition: Mean Absolute Deviation (MAD)

The mean absolute deviation is one way to measure how spread out a data set is. Sometimes we call this the MAD. For example, for the data set 7, 9, 12, 13, 14, the MAD is 2.4. This tells us that these travel times are typically 2.4 minutes away from the mean, which is 11.

To find the MAD, add up the distance between each data point and the mean. Then, divide by how many numbers there are.

\(4+2+1+2+3=12\) and \(12\div 5=2.4\)

Definition: Measure of Center

A measure of center is a value that seems typical for a data distribution.

Mean and median are both measures of center.

Exercise \(\PageIndex{5}\)

Han recorded the number of pages that he read each day for five days. The dot plot shows his data.

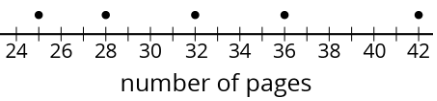
• Is 30 pages a good estimate of the mean number of pages that Han read each day? Explain your reasoning.
• Find the mean number of pages that Han read during the five days. Draw a triangle to mark the mean on the dot plot.
• Calculate the mean absolute deviation (MAD) of the data. Explain or show your reasoning.

Exercise \(\PageIndex{6}\)

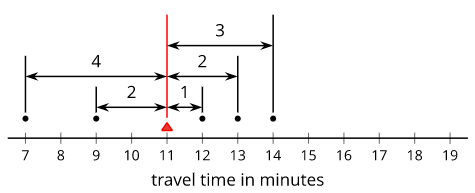
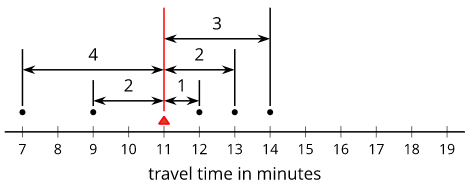
Ten sixth-grade students recorded the amounts of time each took to travel to school. The dot plot shows their travel times.

The mean travel time for these students is approximately 9 minutes. The MAD is approximately 4.2 minutes.​

• Which number of minutes—9 or 4.2—is a typical amount of time for the ten sixth-grade students to travel to school? Explain your reasoning.
• Based on the mean and MAD, Jada believes that travel times between 5 and 13 minutes are common for this group. Do you agree? Explain your reasoning.
• A different group of ten sixth-grade students also recorded their travel times to school. Their mean travel time was also 9 minutes, but the MAD was about 7 minutes. What could the dot plot of this second data set be? Describe or draw how it might look.

Exercise \(\PageIndex{7}\)

In an archery competition, scores for each round are calculated by averaging the distance of 3 arrows from the center of the target.

An archer has a mean distance of 1.6 inches and a MAD distance of 1.3 inches in the first round. In the second round, the archer's arrows are farther from the center but are more consistent. What values for the mean and MAD would fit this description for the second round? Explain your reasoning.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 6th grade   >   Unit 11

Mean absolute deviation (mad).

• Mean absolute deviation example

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Calculating the Mean Absolute Deviation

• Descriptive Statistics
• Statistics Tutorials
• Probability & Games
• Inferential Statistics
• Applications Of Statistics
• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade

Common Uses

• Ph.D., Mathematics, Purdue University
• M.S., Mathematics, Purdue University
• B.A., Mathematics, Physics, and Chemistry, Anderson University

There are many measurements of spread or dispersion in statistics. Although the range and standard deviation are most commonly used, there are other ways to quantify dispersion. We will look at how to calculate the mean absolute deviation for a data set. 

We begin with the definition of the mean absolute deviation, which is also referred to as the average absolute deviation. The formula displayed with this article is the formal definition of the mean absolute deviation. It may make more sense to consider this formula as a process, or series of steps, that we can use to obtain our statistic.

• We start with an average, or measurement of the center , of a data set, which we will denote by m.  
• Next, we find how much each of the data values deviates from m.  This means that we take the difference between each of the data values and m.  
• After this, we take the absolute value of each of the difference from the previous step. In other words, we drop any negative signs for any of the differences. The reason for doing this is that there are positive and negative deviations from m.  If we do not figure out a way to eliminate the negative signs, all of the deviations will cancel one another out if we add them together.
• Now we add together all of these absolute values.
• Finally, we divide this sum by n , which is the total number of data values. The result is the mean absolute deviation.

There are several variations for the above process. Note that we did not specify exactly what m is. The reason for this is that we could use a variety of statistics for m.  Typically this is the center of our data set, and so any of the measurements of central tendency can be used.

The most common statistical measurements of the center of a data set are the mean, median and the mode. Thus any of these could be used as m in the calculation of the mean absolute deviation. This is why it is common to refer to the mean absolute deviation about the mean or the mean absolute deviation about the median. We will see several examples of this.

Example: Mean Absolute Deviation About the Mean

Suppose that we start with the following data set:

1, 2, 2, 3, 5, 7, 7, 7, 7, 9.

The mean of this data set is 5. The following table will organize our work in calculating the mean absolute deviation about the mean. 

We now divide this sum by 10, since there are a total of ten data values. The mean absolute deviation about the mean is 24/10 = 2.4.

Now we start with a different data set:

1, 1, 4, 5, 5, 5, 5, 7, 7, 10.

Just like the previous data set, the mean of this data set is 5. 

Thus the mean absolute deviation about the mean is 18/10 = 1.8. We compare this result to the first example. Although the mean was identical for each of these examples, the data in the first example was more spread out. We see from these two examples that the mean absolute deviation from the first example is greater than the mean absolute deviation from the second example. The greater the mean absolute deviation, the greater the dispersion of our data.

Example: Mean Absolute Deviation About the Median

Start with the same data set as the first example:

The median of the data set is 6. In the following table, we show the details of the calculation of the mean absolute deviation about the median.

Again we divide the total by 10 and obtain a mean average deviation about the median as 24/10 = 2.4.

Start with the same data set as before:

This time we find the mode of this data set to be 7. In the following table, we show the details of the calculation of the mean absolute deviation about the mode.

We divide the sum of the absolute deviations and see that we have a mean absolute deviation about the mode of 22/10 = 2.2.

There are a few basic properties concerning mean absolute deviations

• The mean absolute deviation about the median is always less than or equal to the mean absolute deviation about the mean.
• The standard deviation is greater than or equal to the mean absolute deviation about the mean.
• The mean absolute deviation is sometimes abbreviated by MAD. Unfortunately, this can be ambiguous as MAD may alternately refer to the median absolute deviation.
• The mean absolute deviation for a normal distribution is approximately 0.8 times the size of the standard deviation.

The mean absolute deviation has a few applications. The first application is that this statistic may be used to teach some of the ideas behind the standard deviation . The mean absolute deviation about the mean is much easier to calculate than the standard deviation. It does not require us to square the deviations, and we do not need to find a square root at the end of our calculation. Furthermore, the mean absolute deviation is more intuitively connected to the spread of the data set than what the standard deviation is. This is why the mean absolute deviation is sometimes taught first, before introducing the standard deviation.

Some have gone so far as to argue that the standard deviation should be replaced by the mean absolute deviation. Although the standard deviation is important for scientific and mathematical applications, it is not as intuitive as the mean absolute deviation. For day-to-day applications, the mean absolute deviation is a more tangible way to measure how spread out data are.

• Differences Between Population and Sample Standard Deviations
• Empirical Relationship Between the Mean, Median, and Mode
• What Is the Median?
• The Difference Between Descriptive and Inferential Statistics
• The Difference Between the Mean, Median, and Mode
• How to Calculate a Sample Standard Deviation
• When Is the Standard Deviation Equal to Zero?
• What Is a Range in Statistics?
• How Are Outliers Determined in Statistics?
• How to Calculate Population Standard Deviation
• Sample Standard Deviation Example Problem
• Variance and Standard Deviation
• Calculating the Correlation Coefficient
• What Are the First and Third Quartiles?
• Example of Confidence Interval for a Population Variance

Statistics Worksheets

Practice and master statistics and data concepts with our helpful walkthroughs and downloadable practice worksheets from our team of elite math educators.

Mean Absolute Deviation

By Tina Goosz

Learn about what Mean Absolute Deviation is and how to use it to solve problems. Find the definition, example problems, and practice problems at Thinkster Math.

Why is this concept useful?

Where does this concept fit into the curriculum?

Sample Math Problems

• Downloadable PDFs

Practice Math Problems

How can we use the concept: Most often when finding Mean Absolute Deviation (henceforth called MAD), we follow a series of steps and not a formula.

1) Find the mean of the data set.

2) Find the absolute deviation of each data point by finding the absolute value of the difference between each data point and the mean. (Since we are using absolute value, all these values will be positive.)

3) Find the mean of the deviations.

1. Given the data set: 11, 6, 18, 4, 15, 25 find the mean absolute deviation.

Step 1: Find the mean of the data set.

(11 + 6 + 18 + 4 + 15 + 25) 6 = 13.167 (answer rounded to the thousandths place)

Step 2: Find the absolute value of the difference of each data point from the mean.

| 11 - 13.167 | = 2.167

| 6 - 13.167 |= 7.167

| 18 - 13.167 |= 4.833

| 4 - 13.167 | = 9.167

| 15 - 13.167 |= 1.833

| 25 - 13.167 |= 11.833

Step 3: Find the mean of the deviations.

(2.167 + 7.167 + 4.833 + 9.167 + 1.833 + 11.833) 6 = 6.167

2. Given the data set: 30, 49, 17, 17, 46 find the mean absolute deviation.

(30 + 49 + 17 + 17 + 46) 5 = 31.8

| 30 - 31.8 |= 1.8

| 49 - 31.8 |= 17.2

| 17 - 31.8 |= 14.8 We will use this twice in step 3 of solving since this data point occurs twice in the data set.

|46 - 31.8|= 14.2

(1.8 + 17.2 + 14.8 + 14.8 + 14.2) 5 = 12.56

3. Given the data set: 81, 51, 54, 97, 68, 57, 64 find the mean absolute deviation.

(81 + 51 + 54 + 97 + 68 + 64) 6 = 69.167

| 81 - 69.167 | = 11.833

| 51 - 69.167 | = 18.167

| 54 - 69.167 | = 15.167

| 97 - 69.167 |= 27.833

| 68 - 69.167 |= 1.167

| 64 - 69.167 |= 5.167

(11.833 + 18.167 + 15.167 + 27.833 + 1.167 + 5.167) 6 = 13.22 (rounded)

4. Given the data set: 57, 45.3, 58.2, 46.7, 65.5 find the mean absolute deviation.

(57 + 45.3 + 58.2 + 46.7 + 65.5) 5 = 54.54

| 57 - 54.54 |= 2.46

| 45.3 - 54.54 |= 9.24

| 58.2 - 54.54 |= 3.66

| 46.7 - 54.54 |= 7.84

|65.5 - 54.54 |= 10.96

(2.46 + 9.24 + 3.66 + 7.84 + 10.96) 5 = 6.832

Download FREE Math Resources

Take advantage of our free downloadable resources and study materials for at-home learning.

8 Math Hacks and Tricks to Turn Your ‘Okay’ Math Student Into a Math Champion!

One thing we teach our students at Thinkster is that there are multiple ways to solve a math problem. This helps our students learn to think flexibly and non-linearly.

How to Make Sure Your Child is Highly Successful and Becomes a Millionaire

As a parent, you hope your child is extremely successful and likely become the next Gates, Zuckerberg, or Meg Whitman. To set your child on the right path, there are many skills and traits that you can start building and nurturing now. Doing so plants the seeds for future success.

1. Given the data set: 2, 9, 22, 16, 10, 16 find the mean absolute deviation.

2. Given the data set: 12, 38, 37, 25, 12 find the mean absolute deviation.

3. Given the data set: 75, 72, 85, 91, 74, 81 find the mean absolute deviation.

4. Given the data set: 92.4, 90.5, 100.7, 87.7, 93.2 find the mean absolute deviation.

Kindergarten

Discover More at the Thinkster Blog

Parents like you are always looking for tips, suggestions, and activities to help their child become the best they can be! Learn more from our expert educators by visiting our blog.

Math Tutor and Coaching Program

With personalized attention from elite math tutors, help your child gain confidence in their math skills.

The Book of Secrets

Learn how to Make Your Child Math Fit for Life.

Related Topics

By Puja Varude

Normal Distribution

By Patricia Martin

Tossing a Coin

By Mandi Elam

Properties of Exponents

By Debi DalPezzo

Solve for x

Your child can improve their math scores by 90% within 3 months.

Our elite math tutors are ready to help make your child a math champion! Sign up for our zero $ free trial to get started today.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.2: Measures of Variability

• Last updated
• Save as PDF
• Page ID 35662

• Danielle Navarro
• University of New South Wales

The statistics that we’ve discussed so far all relate to central tendency . That is, they all talk about which values are “in the middle” or “popular” in the data. However, central tendency is not the only type of summary statistic that we want to calculate. The second thing that we really want is a measure of the variability of the data. That is, how “spread out” are the data? How “far” away from the mean or median do the observed values tend to be? For now, let’s assume that the data are interval or ratio scale, so we’ll continue to use the afl.margins data. We’ll use this data to discuss several different measures of spread, each with different strengths and weaknesses.

The range of a variable is very simple: it’s the biggest value minus the smallest value. For the AFL winning margins data, the maximum value is 116, and the minimum value is 0. We can calculate these values in R using the max() and min() functions:

where I’ve omitted the output because it’s not interesting. The other possibility is to use the range() function; which outputs both the minimum value and the maximum value in a vector, like this:

Although the range is the simplest way to quantify the notion of “variability”, it’s one of the worst. Recall from our discussion of the mean that we want our summary measure to be robust. If the data set has one or two extremely bad values in it, we’d like our statistics not to be unduly influenced by these cases. If we look once again at our toy example of a data set containing very extreme outliers…

−100,2,3,4,5,6,7,8,9,10

… it is clear that the range is not robust, since this has a range of 110, but if the outlier were removed we would have a range of only 8.

Interquartile range

The interquartile range (IQR) is like the range, but instead of calculating the difference between the biggest and smallest value, it calculates the difference between the 25th quantile and the 75th quantile. Probably you already know what a quantile is (they’re more commonly called percentiles), but if not: the 10th percentile of a data set is the smallest number x such that 10% of the data is less than x. In fact, we’ve already come across the idea: the median of a data set is its 50th quantile / percentile! R actually provides you with a way of calculating quantiles, using the (surprise, surprise) quantile() function. Let’s use it to calculate the median AFL winning margin:

And not surprisingly, this agrees with the answer that we saw earlier with the median() function. Now, we can actually input lots of quantiles at once, by specifying a vector for the probs argument. So lets do that, and get the 25th and 75th percentile:

And, by noting that 50.5−12.75=37.75, we can see that the interquartile range for the 2010 AFL winning margins data is 37.75. Of course, that seems like too much work to do all that typing, so R has a built in function called IQR() that we can use:

While it’s obvious how to interpret the range, it’s a little less obvious how to interpret the IQR. The simplest way to think about it is like this: the interquartile range is the range spanned by the “middle half” of the data. That is, one quarter of the data falls below the 25th percentile, one quarter of the data is above the 75th percentile, leaving the “middle half” of the data lying in between the two. And the IQR is the range covered by that middle half.

Mean absolute deviation

The two measures we’ve looked at so far, the range and the interquartile range, both rely on the idea that we can measure the spread of the data by looking at the quantiles of the data. However, this isn’t the only way to think about the problem. A different approach is to select a meaningful reference point (usually the mean or the median) and then report the “typical” deviations from that reference point. What do we mean by “typical” deviation? Usually, the mean or median value of these deviations! In practice, this leads to two different measures, the “mean absolute deviation (from the mean)” and the “median absolute deviation (from the median)”. From what I’ve read, the measure based on the median seems to be used in statistics, and does seem to be the better of the two, but to be honest I don’t think I’ve seen it used much in psychology. The measure based on the mean does occasionally show up in psychology though. In this section I’ll talk about the first one, and I’ll come back to talk about the second one later.

Since the previous paragraph might sound a little abstract, let’s go through the mean absolute deviation from the mean a little more slowly. One useful thing about this measure is that the name actually tells you exactly how to calculate it. Let’s think about our AFL winning margins data, and once again we’ll start by pretending that there’s only 5 games in total, with winning margins of 56, 31, 56, 8 and 32. Since our calculations rely on an examination of the deviation from some reference point (in this case the mean), the first thing we need to calculate is the mean, \(\bar{X}\). For these five observations, our mean is \(\bar{X}\)=36.6. The next step is to convert each of our observations X i into a deviation score. We do this by calculating the difference between the observation Xi and the mean \(\bar{X}\). That is, the deviation score is defined to be X i −\(\bar{X}\). For the first observation in our sample, this is equal to 56−36.6=19.4. Okay, that’s simple enough. The next step in the process is to convert these deviations to absolute deviations. As we discussed earlier when talking about the abs() function in R (Section 3.5), we do this by converting any negative values to positive ones. Mathematically, we would denote the absolute value of −3 as |−3|, and so we say that |−3|=3. We use the absolute value function here because we don’t really care whether the value is higher than the mean or lower than the mean, we’re just interested in how close it is to the mean. To help make this process as obvious as possible, the table below shows these calculations for all five observations:

Now that we have calculated the absolute deviation score for every observation in the data set, all that we have to do to calculate the mean of these scores. Let’s do that:

\[ \dfrac{19.4+5.6+19.4+28.6+4.6}{5}=15.52 \nonumber\]

And we’re done. The mean absolute deviation for these five scores is 15.52.

However, while our calculations for this little example are at an end, we do have a couple of things left to talk about. Firstly, we should really try to write down a proper mathematical formula. But in order do to this I need some mathematical notation to refer to the mean absolute deviation. Irritatingly, “mean absolute deviation” and “median absolute deviation” have the same acronym (MAD), which leads to a certain amount of ambiguity, and since R tends to use MAD to refer to the median absolute deviation, I’d better come up with something different for the mean absolute deviation. Sigh. What I’ll do is use AAD instead, short for average absolute deviation. Now that we have some unambiguous notation, here’s the formula that describes what we just calculated:

\[ (X)=\dfrac{1}{N} \sum_{i=1}^{N}\left|X_{i}-\bar{X}\right| \nonumber\]

The last thing we need to talk about is how to calculate AAD in R. One possibility would be to do everything using low level commands, laboriously following the same steps that I used when describing the calculations above. However, that’s pretty tedious. You’d end up with a series of commands that might look like this:

Each of those commands is pretty simple, but there’s just too many of them. And because I find that to be too much typing, the lsr package has a very simple function called aad() that does the calculations for you. If we apply the aad() function to our data, we get this:

No suprises there.

Although the mean absolute deviation measure has its uses, it’s not the best measure of variability to use. From a purely mathematical perspective, there are some solid reasons to prefer squared deviations rather than absolute deviations. If we do that, we obtain a measure is called the variance , which has a lot of really nice statistical properties that I’m going to ignore, 71 (X)$ and Var(Y) respectively. Now imagine I want to define a new variable Z that is the sum of the two, Z=X+Y. As it turns out, the variance of Z is equal to Var(X)+Var(Y). This is a very useful property, but it’s not true of the other measures that I talk about in this section.] and one massive psychological flaw that I’m going to make a big deal out of in a moment. The variance of a data set X is sometimes written as Var(X), but it’s more commonly denoted s 2 (the reason for this will become clearer shortly). The formula that we use to calculate the variance of a set of observations is as follows:

\[ \begin{aligned} &\operatorname{Var}(X)=\dfrac{1}{N} \sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}\\ &\operatorname{Var}(X)=\dfrac{\sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}}{N} \end{aligned} \nonumber\]

As you can see, it’s basically the same formula that we used to calculate the mean absolute deviation, except that instead of using “absolute deviations” we use “squared deviations”. It is for this reason that the variance is sometimes referred to as the “mean square deviation”.

Now that we’ve got the basic idea, let’s have a look at a concrete example. Once again, let’s use the first five AFL games as our data. If we follow the same approach that we took last time, we end up with the following table:

Table 5.1: Basic arithmetic operations in R. These five operators are used very frequently throughout the text, so it’s important to be familiar with them at the outset.

That last column contains all of our squared deviations, so all we have to do is average them. If we do that by typing all the numbers into R by hand…

… we end up with a variance of 324.64. Exciting, isn’t it? For the moment, let’s ignore the burning question that you’re all probably thinking (i.e., what the heck does a variance of 324.64 actually mean?) and instead talk a bit more about how to do the calculations in R, because this will reveal something very weird.

As always, we want to avoid having to type in a whole lot of numbers ourselves. And as it happens, we have the vector X lying around, which we created in the previous section. With this in mind, we can calculate the variance of X by using the following command,

and as usual we get the same answer as the one that we got when we did everything by hand. However, I still think that this is too much typing. Fortunately, R has a built in function called var() which does calculate variances. So we could also do this…

and you get the same… no, wait… you get a completely different answer. That’s just weird. Is R broken? Is this a typo? Is Dan an idiot?

As it happens, the answer is no. 72 It’s not a typo, and R is not making a mistake. To get a feel for what’s happening, let’s stop using the tiny data set containing only 5 data points, and switch to the full set of 176 games that we’ve got stored in our afl.margins vector. First, let’s calculate the variance by using the formula that I described above:

Now let’s use the var() function:

Hm. These two numbers are very similar this time. That seems like too much of a coincidence to be a mistake. And of course it isn’t a mistake. In fact, it’s very simple to explain what R is doing here, but slightly trickier to explain why R is doing it. So let’s start with the “what”. What R is doing is evaluating a slightly different formula to the one I showed you above. Instead of averaging the squared deviations, which requires you to divide by the number of data points N, R has chosen to divide by N−1. In other words, the formula that R is using is this one

\[ \dfrac{1}{N-1} \sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2} \nonumber\]

It’s easy enough to verify that this is what’s happening, as the following command illustrates:

This is the same answer that R gave us originally when we calculated var(X) originally. So that’s the what . The real question is why R is dividing by N−1 and not by N. After all, the variance is supposed to be the mean squared deviation, right? So shouldn’t we be dividing by N, the actual number of observations in the sample? Well, yes, we should. However, as we’ll discuss in Chapter 10, there’s a subtle distinction between “describing a sample” and “making guesses about the population from which the sample came”. Up to this point, it’s been a distinction without a difference. Regardless of whether you’re describing a sample or drawing inferences about the population, the mean is calculated exactly the same way. Not so for the variance, or the standard deviation, or for many other measures besides. What I outlined to you initially (i.e., take the actual average, and thus divide by N) assumes that you literally intend to calculate the variance of the sample. Most of the time, however, you’re not terribly interested in the sample in and of itself . Rather, the sample exists to tell you something about the world. If so, you’re actually starting to move away from calculating a “sample statistic”, and towards the idea of estimating a “population parameter”. However, I’m getting ahead of myself. For now, let’s just take it on faith that R knows what it’s doing, and we’ll revisit the question later on when we talk about estimation in Chapter 10.

Okay, one last thing. This section so far has read a bit like a mystery novel. I’ve shown you how to calculate the variance, described the weird “N−1” thing that R does and hinted at the reason why it’s there, but I haven’t mentioned the single most important thing… how do you interpret the variance? Descriptive statistics are supposed to describe things, after all, and right now the variance is really just a gibberish number. Unfortunately, the reason why I haven’t given you the human-friendly interpretation of the variance is that there really isn’t one. This is the most serious problem with the variance. Although it has some elegant mathematical properties that suggest that it really is a fundamental quantity for expressing variation, it’s completely useless if you want to communicate with an actual human… variances are completely uninterpretable in terms of the original variable! All the numbers have been squared, and they don’t mean anything anymore. This is a huge issue. For instance, according to the table I presented earlier, the margin in game 1 was “376.36 points-squared higher than the average margin”. This is exactly as stupid as it sounds; and so when we calculate a variance of 324.64, we’re in the same situation. I’ve watched a lot of footy games, and never has anyone referred to “points squared”. It’s not a real unit of measurement, and since the variance is expressed in terms of this gibberish unit, it is totally meaningless to a human.

Standard deviation

Okay, suppose that you like the idea of using the variance because of those nice mathematical properties that I haven’t talked about, but – since you’re a human and not a robot – you’d like to have a measure that is expressed in the same units as the data itself (i.e., points, not points-squared). What should you do? The solution to the problem is obvious: take the square root of the variance, known as the standard deviation , also called the “root mean squared deviation”, or RMSD. This solves out problem fairly neatly: while nobody has a clue what “a variance of 324.68 points-squared” really means, it’s much easier to understand “a standard deviation of 18.01 points”, since it’s expressed in the original units. It is traditional to refer to the standard deviation of a sample of data as s, though “sd” and “std dev.” are also used at times. Because the standard deviation is equal to the square root of the variance, you probably won’t be surprised to see that the formula is:

\[ s=\sqrt{\dfrac{1}{N} \sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}} \nonumber\]

and the R function that we use to calculate it is sd() . However, as you might have guessed from our discussion of the variance, what R actually calculates is slightly different to the formula given above. Just like the we saw with the variance, what R calculates is a version that divides by N−1 rather than N. For reasons that will make sense when we return to this topic in Chapter@refch:estimation I’ll refer to this new quantity as \(\hat{\sigma}\) (read as: “sigma hat”), and the formula for this is

\[ \hat{\sigma}=\sqrt{\dfrac{1}{N-1} \sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}} \nonumber\]

With that in mind, calculating standard deviations in R is simple:

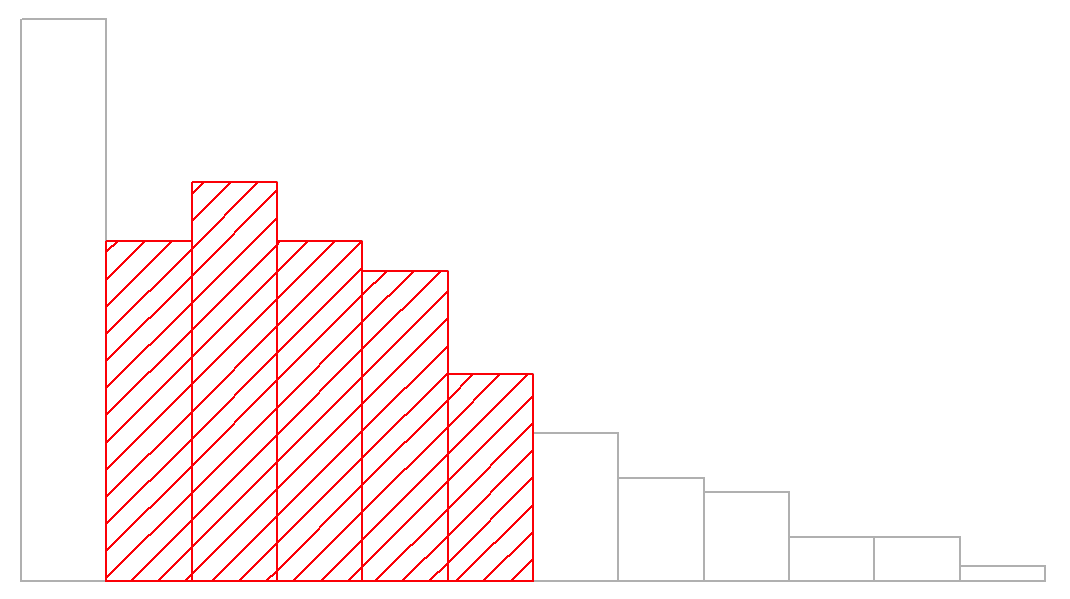
Interpreting standard deviations is slightly more complex. Because the standard deviation is derived from the variance, and the variance is a quantity that has little to no meaning that makes sense to us humans, the standard deviation doesn’t have a simple interpretation. As a consequence, most of us just rely on a simple rule of thumb: in general, you should expect 68% of the data to fall within 1 standard deviation of the mean, 95% of the data to fall within 2 standard deviation of the mean, and 99.7% of the data to fall within 3 standard deviations of the mean. This rule tends to work pretty well most of the time, but it’s not exact: it’s actually calculated based on an assumption that the histogram is symmetric and “bell shaped.” 73 As you can tell from looking at the AFL winning margins histogram in Figure 5.1, this isn’t exactly true of our data! Even so, the rule is approximately correct. As it turns out, 65.3% of the AFL margins data fall within one standard deviation of the mean. This is shown visually in Figure 5.3.

Median absolute deviation

The last measure of variability that I want to talk about is the median absolute deviation (MAD). The basic idea behind MAD is very simple, and is pretty much identical to the idea behind the mean absolute deviation (Section 5.2.3). The difference is that you use the median everywhere. If we were to frame this idea as a pair of R commands, they would look like this:

This has a straightforward interpretation: every observation in the data set lies some distance away from the typical value (the median). So the MAD is an attempt to describe a typical deviation from a typical value in the data set. It wouldn’t be unreasonable to interpret the MAD value of 19.5 for our AFL data by saying something like this:

The median winning margin in 2010 was 30.5, indicating that a typical game involved a winning margin of about 30 points. However, there was a fair amount of variation from game to game: the MAD value was 19.5, indicating that a typical winning margin would differ from this median value by about 19-20 points.

As you’d expect, R has a built in function for calculating MAD, and you will be shocked no doubt to hear that it’s called mad() . However, it’s a little bit more complicated than the functions that we’ve been using previously. If you want to use it to calculate MAD in the exact same way that I have described it above, the command that you need to use specifies two arguments: the data set itself x , and a constant that I’ll explain in a moment. For our purposes, the constant is 1, so our command becomes

Apart from the weirdness of having to type that constant = 1 part, this is pretty straightforward.

Okay, so what exactly is this constant = 1 argument? I won’t go into all the details here, but here’s the gist. Although the “raw” MAD value that I’ve described above is completely interpretable on its own terms, that’s not actually how it’s used in a lot of real world contexts. Instead, what happens a lot is that the researcher actually wants to calculate the standard deviation. However, in the same way that the mean is very sensitive to extreme values, the standard deviation is vulnerable to the exact same issue. So, in much the same way that people sometimes use the median as a “robust” way of calculating “something that is like the mean”, it’s not uncommon to use MAD as a method for calculating “something that is like the standard deviation”. Unfortunately, the raw MAD value doesn’t do this. Our raw MAD value is 19.5, and our standard deviation was 26.07. However, what some clever person has shown is that, under certain assumptions 74 , you can multiply the raw MAD value by 1.4826 and obtain a number that is directly comparable to the standard deviation. As a consequence, the default value of constant is 1.4826, and so when you use the mad() command without manually setting a value, here’s what you get:

I should point out, though, that if you want to use this “corrected” MAD value as a robust version of the standard deviation, you really are relying on the assumption that the data are (or at least, are “supposed to be” in some sense) symmetric and basically shaped like a bell curve. That’s really not true for our afl.margins data, so in this case I wouldn’t try to use the MAD value this way.

Which measure to use?

We’ve discussed quite a few measures of spread (range, IQR, MAD, variance and standard deviation), and hinted at their strengths and weaknesses. Here’s a quick summary:

• Range . Gives you the full spread of the data. It’s very vulnerable to outliers, and as a consequence it isn’t often used unless you have good reasons to care about the extremes in the data.
• Interquartile range . Tells you where the “middle half” of the data sits. It’s pretty robust, and complements the median nicely. This is used a lot.
• Mean absolute deviation . Tells you how far “on average” the observations are from the mean. It’s very interpretable, but has a few minor issues (not discussed here) that make it less attractive to statisticians than the standard deviation. Used sometimes, but not often.
• Variance . Tells you the average squared deviation from the mean. It’s mathematically elegant, and is probably the “right” way to describe variation around the mean, but it’s completely uninterpretable because it doesn’t use the same units as the data. Almost never used except as a mathematical tool; but it’s buried “under the hood” of a very large number of statistical tools.
• Standard deviation . This is the square root of the variance. It’s fairly elegant mathematically, and it’s expressed in the same units as the data so it can be interpreted pretty well. In situations where the mean is the measure of central tendency, this is the default. This is by far the most popular measure of variation.
• Median absolute deviation . The typical (i.e., median) deviation from the median value. In the raw form it’s simple and interpretable; in the corrected form it’s a robust way to estimate the standard deviation, for some kinds of data sets. Not used very often, but it does get reported sometimes.

In short, the IQR and the standard deviation are easily the two most common measures used to report the variability of the data; but there are situations in which the others are used. I’ve described all of them in this book because there’s a fair chance you’ll run into most of these somewhere.

• Math Article

Mean Absolute Deviation

To understand Mean Absolute Deviation,  let us split both the words and try to figure out their meaning. ‘Mean’ refers to the average of the observations and deviation implies departure or variation from a preset standard.

When put together, we can define mean deviation as the mean distance of each observation from the mean of the data.

Mean Absolute Deviation Formula

Ratio of sum of all absolute values of deviation from central measure to the total number of observations.

M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)

Calculate Mean Absolute Deviation

Steps to find the mean deviation from mean:

(i)Find the mean of the given observations.

(ii)Calculate the difference between each observation and the calculated mean

(iii)Evaluate the mean of the differences obtained in the second step.

This gives you the mean deviation from mean.

Suppose that the deviation from a central value a is given as (x-a), where x is any observation of the set of data. To find out the mean deviation, we need to find the average of all the deviations from a in the given data set. Since the measure of central tendency lies between the maximum and minimum values of the data set,we can see that some deviations would be positive and rest would be negative.The sum of such deviations would give a zero. Let us see an example to make this point clearer to you.

Consider the following data set

The mean of the given data is given as:

\(\begin{array}{l}\overline{x}\end{array} \) = \(\begin{array}{l}\frac{\sum\limits_{i=1}{n}x_i}{n}\end{array} \)

\(\begin{array}{l} \Rightarrow \overline{x} \end{array} \) = \(\begin{array}{l} \frac{85 + 75 + 80}{3} \end{array} \) = \(\begin{array}{l} 80 \end{array} \)

Now, if we calculate the deviation from mean for the given values, we have:

From the definition , we have

\(\begin{array}{l}Mean~ Deviation\end{array} \) = \(\begin{array}{l} \frac{Sum~ of~ all~ the~ deviations~ from~ mean}{Total ~number~ of ~observations}\end{array} \)

\(\begin{array}{l}\Rightarrow Mean~ Deviation\end{array} \) = \(\begin{array}{l}{5+(-5)+0} \end{array} \) = \(\begin{array}{l}0\end{array} \)

This does not give us any idea about measure of variability of the data which is the actual purpose of finding the mean deviation. So, we find the absolute value of deviation from the mean.

In the above example the mean absolute deviation can be calculated as:

\(\begin{array}{l}Mean ~Absolute~ Deviation~(M.A.D)\end{array} \) = \(\begin{array}{l}\frac{5+|-5|+0}{3}\end{array} \) = \(\begin{array}{l}\frac{10}{3}\end{array} \) = \(\begin{array}{l}3.333\end{array} \)

This gives us an idea about the deviation of the observations from the measure of central tendency.

Thus we can conclude that,

\(\begin{array}{l}M.A.D\end{array} \) = \(\begin{array}{l}\frac{∑Absolute ~values ~of ~Deviation ~from ~cental~ measure}{Total~ Number~ of ~observations}\end{array} \)

Although to calculate mean absolute deviation, any measure of central tendency can be used but generally mean and median are the most common ones.

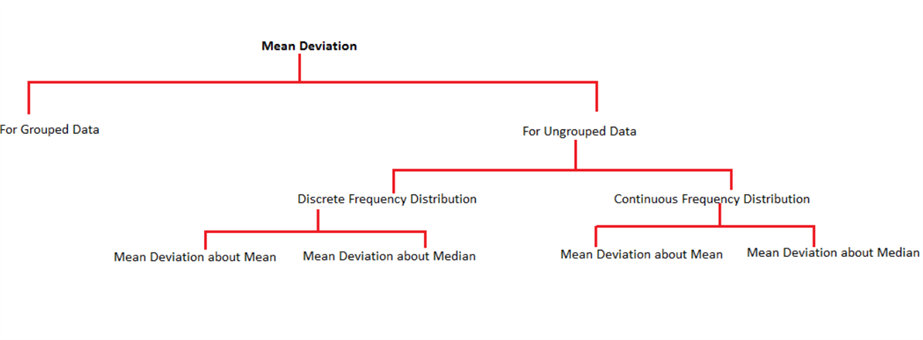
In the upcoming discussions, we will be discussing about calculating deviations for various types of data. The following diagram represents the methods to calculate the mean deviation from mean for two types of data, i.e. grouped and ungrouped data.

Now, you are clear about mean absolute deviation, download Byju’s-the learning app.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Absolute Deviation & Variance

Quartiles are useful, but they are also somewhat limited because they do not take into account every score in our group of data. To get a more representative idea of spread we need to take into account the actual values of each score in a data set. The absolute deviation, variance and standard deviation are such measures.

The absolute and mean absolute deviation show the amount of deviation (variation) that occurs around the mean score. To find the total variability in our group of data, we simply add up the deviation of each score from the mean. The average deviation of a score can then be calculated by dividing this total by the number of scores. How we calculate the deviation of a score from the mean depends on our choice of statistic, whether we use absolute deviation, variance or standard deviation .

Absolute Deviation and Mean Absolute Deviation

Perhaps the simplest way of calculating the deviation of a score from the mean is to take each score and minus the mean score. For example, the mean score for the group of 100 students we used earlier was 58.75 out of 100. Therefore, if we took a student that scored 60 out of 100, the deviation of a score from the mean is 60 - 58.75 = 1.25. It is important to note that scores above the mean have positive deviations (as demonstrated above), whilst scores below the mean will have negative deviations.

To find out the total variability in our data set, we would perform this calculation for all of the 100 students' scores. However, the problem is that because we have both positive and minus signs, when we add up all of these deviations, they cancel each other out, giving us a total deviation of zero. Since we are only interested in the deviations of the scores and not whether they are above or below the mean score, we can ignore the minus sign and take only the absolute value, giving us the absolute deviation . Adding up all of these absolute deviations and dividing them by the total number of scores then gives us the mean absolute deviation (see below). Therefore, for our 100 students the mean absolute deviation is 12.81, as shown below:

Another method for calculating the deviation of a group of scores from the mean, such as the 100 students we used earlier, is to use the variance. Unlike the absolute deviation, which uses the absolute value of the deviation in order to "rid itself" of the negative values, the variance achieves positive values by squaring each of the deviations instead. Adding up these squared deviations gives us the sum of squares, which we can then divide by the total number of scores in our group of data (in other words, 100 because there are 100 students) to find the variance (see below). Therefore, for our 100 students, the variance is 211.89, as shown below:

As a measure of variability, the variance is useful. If the scores in our group of data are spread out, the variance will be a large number. Conversely, if the scores are spread closely around the mean, the variance will be a smaller number. However, there are two potential problems with the variance. First, because the deviations of scores from the mean are 'squared', this gives more weight to extreme scores. If our data contains outliers (in other words, one or a small number of scores that are particularly far away from the mean and perhaps do not represent well our data as a whole), this can give undo weight to these scores. Secondly, the variance is not in the same units as the scores in our data set: variance is measured in the units squared. This means we cannot place it on our frequency distribution and cannot directly relate its value to the values in our data set. Therefore, the figure of 211.89, our variance, appears somewhat arbitrary. Calculating the standard deviation rather than the variance rectifies this problem. Nonetheless, analysing variance is extremely important in some statistical analyses, discussed in other statistical guides.

Engage your students with effective distance learning resources. ACCESS RESOURCES>>

Math homework problems.

Over a two week period, Jenna had the following number of math homework problems given each day:$$20,\,0,\,7,\,10,\,1,\,11,\,0,\,25,\,15,\,1.$$

• What is the mean number of homework problems Jenna had?
• What is the Mean Absolute Deviation for the number of homework problems?
• What do the mean and Mean Absolute Deviation tell you about the number of homework problems Jenna had over these two weeks?

IM Commentary

The goal of this task is to calculate and interpret the Mean Absolute Deviation in a context. It is intended to be an introductory task but can readily be adapted for a more in depth study. The teacher may wish to have students make a dot plot of the data or analyze the quartiles and create a box plot. The data set is peculiar in that it roughly divides into three separate parts: the days (4) when there is little or no homework, the days (3) when there is a moderate number of homework problems, and the days (3) when the assignment is relatively large. Teachers may wish to have students discuss  why  homework assignments might have this structure: for example, the assignments with only one question are likely challenging problems, perhaps involving modeling or work outside of class. Or there may be an upcoming exam so students are given more time to prepare. The large assignments are likely more routine problems while the days when no homework is assigned the class is probably wrapping up previous material. 

Teachers may prefer to substitute actual data from their own class. Alternatively, they could examine and compare data from different math classes. A follow-up challenging question would be: how much flexibility is there in the data if the mean is 8 and the Mean Absolute Deviation is 7.2? In other words, how much information do these statistics tell us about the actual data?

• To calculate the mean, we first find the total number of homework problems assigned: $$20 + 0 + 7 + 10 + 1 + 11 + 0 + 25 + 15 + 1 = 90.$$ There were 10 homework assignments so the mean number of homework problems is 90 $\div$ 10 = 9.

If we add the numbers in the last column we get 72. There are 10 assignments so the Mean Absolute Deviation is 72 $\div$ 10 = 7.2.

The mean is 9 and the Mean Absolute Deviation is 7.2. The mean tells us the average number of homework problems Jenna had each day. The Mean Absolute Deviation is almost as large as the mean so this tells us that there is substantial variation in the number of homework problems assigned each day: some days there are a lot more than the mean of 9 and some days there are a lot less.  

Mean Calculator

Enter the set of numbers below for which you want to find the mean.

The mean calculator finds the mean of a given set of numbers.

The mean of a set of numbers is given by the formula-

Where , x i is the i th observation and n is the number of observations

Click the blue arrow to submit. Choose "Find the Mean" from the topic selector and click to see the result in our Statistics Calculator!

Find the Mean Find the Mean

Popular Problems

Find the Mean (Arithmetic) 70 , 47 , 70 , 92 , 47 Find the Mean (Arithmetic) 4 , 6 , 10 , 3 , 5 Find the Mean (Arithmetic) 58 , 48 , 49 , 61 , 58 , 51 , 39 Find the Mean (Arithmetic) 101 , 102 , 103 , 104 , 105 , 106 , 107 , 108 , 109 , 110 , 111 , 112 Find the Mean (Arithmetic) 6 , 7 , 9 , 9 , 5

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&