maths assignment on probability

Probability  means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one. Probability has been introduced in Maths to predict how likely events are to happen. The meaning of probability is basically the extent to which something is likely to happen. This is the basic probability theory, which is also used in the  probability distribution , where you will learn the possibility of outcomes for a random experiment. To find the probability of a single event to occur, first, we should know the total number of possible outcomes.

Learn More here: Study Mathematics

Probability Definition in Math

Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e., how likely they are going to happen, using it. Probability can range from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event. Probability for Class 10 is an important topic for the students which explains all the basic concepts of this topic. The probability of all the events in a sample space adds up to 1.

For example , when we toss a coin, either we get Head OR Tail, only two possible outcomes are possible (H, T). But when two coins are tossed then there will be four possible outcomes,  i.e {(H, H), (H, T), (T, H),  (T, T)}.

Download this lesson as PDF: – Download PDF Here

Formula for Probability

The probability formula is defined as the possibility of an event to happen is equal to the ratio of the number of favourable outcomes and the total number of outcomes.

Sometimes students get mistaken for “favourable outcome” with “desirable outcome”. This is the basic formula. But there are some more formulas for different situations or events.

Solved Examples

1) There are 6 pillows in a bed, 3 are red, 2 are yellow and 1 is blue. What is the probability of picking a yellow pillow?

Ans: The probability is equal to the number of yellow pillows in the bed divided by the total number of pillows, i.e. 2/6 = 1/3.

2) There is a container full of coloured bottles, red, blue, green and orange. Some of the bottles are picked out and displaced. Sumit did this 1000 times and got the following results:

• No. of blue bottles picked out: 300
• No. of red bottles: 200
• No. of green bottles: 450
• No. of orange bottles: 50

a) What is the probability that Sumit will pick a green bottle?

Ans: For every 1000 bottles picked out, 450 are green.

Therefore, P(green) = 450/1000 = 0.45

b) If there are 100 bottles in the container, how many of them are likely to be green?

Ans: The experiment implies that 450 out of 1000 bottles are green.

Therefore, out of 100 bottles, 45 are green.

Probability Tree

The tree diagram helps to organize and visualize the different possible outcomes. Branches and ends of the tree are two main positions. Probability of each branch is written on the branch, whereas the ends are containing the final outcome. Tree diagrams are used to figure out when to multiply and when to add. You can see below a tree diagram for the coin:

Types of Probability

There are three major types of probabilities:

Theoretical Probability

Experimental probability, axiomatic probability.

It is based on the possible chances of something to happen. The theoretical probability is mainly based on the reasoning behind probability. For example, if a coin is tossed, the theoretical probability of getting a head will be ½.

It is based on the basis of the observations of an experiment. The experimental probability can be calculated based on the number of possible outcomes by the total number of trials. For example, if a coin is tossed 10 times and head is recorded 6 times then, the experimental probability for heads is 6/10 or, 3/5.

In axiomatic probability, a set of rules or axioms are set which applies to all types. These axioms are set by Kolmogorov and are known as Kolmogorov’s three axioms. With the axiomatic approach to probability, the chances of occurrence or non-occurrence of the events can be quantified. The axiomatic probability lesson covers this concept in detail with Kolmogorov’s three rules (axioms) along with various examples.

Conditional Probability is the likelihood of an event or outcome occurring based on the occurrence of a previous event or outcome.

Probability of an Event

Assume an event E can occur in r ways out of a sum of n probable or possible equally likely ways . Then the probability of happening of the event or its success is expressed as;

The probability that the event will not occur or known as its failure is expressed as:

P(E’) = (n-r)/n = 1-(r/n)

E’ represents that the event will not occur.

Therefore, now we can say;

P(E) + P(E’) = 1

This means that the total of all the probabilities in any random test or experiment is equal to 1.

What are Equally Likely Events?

When the events have the same theoretical probability of happening, then they are called equally likely events. The results of a sample space are called equally likely if all of them have the same probability of occurring. For example, if you throw a die, then the probability of getting 1 is 1/6. Similarly, the probability of getting all the numbers from 2,3,4,5 and 6, one at a time is 1/6. Hence, the following are some examples of equally likely events when throwing a die:

• Getting 3 and 5 on throwing a die
• Getting an even number and an odd number on a die
• Getting 1, 2 or 3 on rolling a die

are equally likely events, since the probabilities of each event are equal.

Complementary Events

The possibility that there will be only two outcomes which states that an event will occur or not. Like a person will come or not come to your house, getting a job or not getting a job, etc. are examples of complementary events. Basically, the complement of an event occurring in the exact opposite that the probability of it is not occurring. Some more examples are:

• It will rain or not rain today
• The student will pass the exam or not pass.
• You win the lottery or you don’t.

Also, read: 

• Independent Events
• Mutually Exclusive Events

Probability Theory

Probability theory had its root in the 16th century when J. Cardan, an Italian mathematician and physician, addressed the first work on the topic, The Book on Games of Chance. After its inception, the knowledge of probability has brought to the attention of great mathematicians. Thus, Probability theory is the branch of mathematics that deals with the possibility of the happening of events. Although there are many distinct probability interpretations, probability theory interprets the concept precisely by expressing it through a set of axioms or hypotheses. These hypotheses help form the probability in terms of a possibility space, which allows a measure holding values between 0 and 1. This is known as the probability measure, to a set of possible outcomes of the sample space.

Probability Density Function

The Probability Density Function (PDF) is the probability function which is represented for the density of a continuous random variable lying between a certain range of values. Probability Density Function explains the normal distribution and how mean and deviation exists. The standard normal distribution is used to create a database or statistics, which are often used in science to represent the real-valued variables, whose distribution is not known.

Probability Terms and Definition

Some of the important probability terms are discussed here:

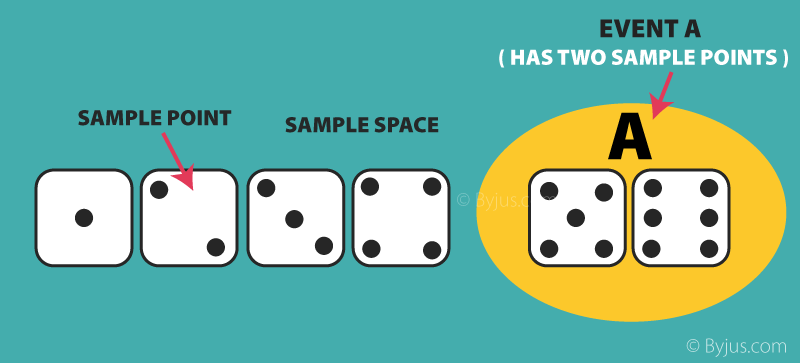
Applications of Probability

Probability has a wide variety of applications in real life. Some of the common applications which we see in our everyday life while checking the results of the following events:

• Choosing a card from the deck of cards
• Flipping a coin
• Throwing a dice in the air
• Pulling a red ball out of a bucket of red and white balls
• Winning a lucky draw

Other Major Applications of Probability

• It is used for risk assessment and modelling in various industries
• Weather forecasting or prediction of weather changes
• Probability of a team winning in a sport based on players and strength of team
• In the share market, chances of getting the hike of share prices

Problems and Solutions on Probability

Question 1: Find the probability of ‘getting 3 on rolling a die’.

Sample Space = S = {1, 2, 3, 4, 5, 6}

Total number of outcomes = n(S) = 6

Let A be the event of getting 3.

Number of favourable outcomes = n(A) = 1

i.e. A  = {3}

Probability, P(A) = n(A)/n(S) = 1/6

Hence, P(getting 3 on rolling a die) = 1/6

Question 2: Draw a random card from a pack of cards. What is the probability that the card drawn is a face card?

A standard deck has 52 cards.

Total number of outcomes = n(S) = 52

Let E be the event of drawing a face card.

Number of favourable events = n(E) = 4 x 3 = 12 (considered Jack, Queen and King only)

Probability, P = Number of Favourable Outcomes/Total Number of Outcomes

P(E) = n(E)/n(S)

P(the card drawn is a face card) = 3/13

Question 3: A vessel contains 4 blue balls, 5 red balls and 11 white balls. If three balls are drawn from the vessel at random, what is the probability that the first ball is red, the second ball is blue, and the third ball is white?

The probability to get the first ball is red or the first event is 5/20.

Since we have drawn a ball for the first event to occur, then the number of possibilities left for the second event to occur is 20 – 1 = 19.

Hence, the probability of getting the second ball as blue or the second event is 4/19.

Again with the first and second event occurring, the number of possibilities left for the third event to occur is 19 – 1 = 18.

And the probability of the third ball is white or the third event is 11/18.

Therefore, the probability is 5/20 x 4/19 x 11/18 = 44/1368 = 0.032.

Or we can express it as: P = 3.2%.

Question 4: Two dice are rolled, find the probability that the sum is:

• less than 13

Video Lectures

Introduction.

Solving Probability Questions

Probability Important Topics

Probability Important Questions

Probability Problems

• Two dice are thrown together. Find the probability that the product of the numbers on the top of the dice is: (i) 6 (ii) 12 (iii) 7
• A bag contains 10 red, 5 blue and 7 green balls. A ball is drawn at random. Find the probability of this ball being a (i) red ball (ii) green ball (iii) not a blue ball
• All the jacks, queens and kings are removed from a deck of 52 playing cards. The remaining cards are well shuffled and then one card is drawn at random. Giving ace a value 1 similar value for other cards, find the probability that the card has a value (i) 7 (ii) greater than 7 (iii) less than 7
• A die has its six faces marked 0, 1, 1, 1, 6, 6. Two such dice are thrown together and the total score is recorded. (i) How many different scores are possible? (ii) What is the probability of getting a total of 7?

Frequently Asked Questions (FAQs) on Probability

What is probability give an example, what is the formula of probability, what are the different types of probability, what are the basic rules of probability, what is the complement rule in probability.

In probability, the complement rule states that “the sum of probabilities of an event and its complement should be equal to 1”. If A is an event, then the complement rule is given as: P(A) + P(A’) = 1.

What are the different ways to present the probability value?

The three ways to present the probability values are:

• Decimal or fraction

What does the probability of 0 represent?

The probability of 0 represents that the event will not happen or that it is an impossible event.

What is the sample space for tossing two coins?

The sample space for tossing two coins is: S = {HH, HT, TH, TT}

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

good basics concepts provide

Great video content. Perfectly explained for examinations. I really like to learn from BYJU’s

Thank you for your best information on probablity

Good explanation about probability and concept for simple understanding the overall chapter. I hope this is a good way to understand the CONCEPT

For learner of class X standard , it is providing all the relevant informations and approach towards the contenet is knitted in an elegant manner and students will have the opportunity to grasp the topic easily and will be immensely benefited.

this topic has been hard for me but now I know what it is all about and I have really enjoyed it thanks for your good explanation

Well explained

Excellent explanation of probability. One can easily understand about the probability.

I really appreciated your explanations because it’s well understandable Thanks

Love the way you teach

There are 3 boxes Box A contains 10 bulbs out of which 4 are dead box b contains 6 bulbs out of which 1 is dead box c contains 8 bulbs out of which 3 are dead. If a dead bulb is picked at random find the probability that it is from which box?

Probability of selecting a dead bulb from the first box = (1/3) x (4/10) = 4/30 Probability of selecting a dead bulb from the second box = (1/3) x (1/6) = 1/18 Probability of selecting a dead bulb from the third box = (1/3) x (3/8) = 3/24 = 1/8 Total probability = (4/30) + (1/18) + (1/8) = (48 + 20 + 45)360 =113/360

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Probability

How likely something is to happen.

Many events can't be predicted with total certainty. The best we can say is how likely they are to happen, using the idea of probability.

Tossing a Coin

When a coin is tossed, there are two possible outcomes:

Heads (H) or Tails (T)

• the probability of the coin landing H is ½
• the probability of the coin landing T is ½

Throwing Dice

When a single die is thrown, there are six possible outcomes: 1, 2, 3, 4, 5, 6 .

The probability of any one of them is 1 6

In general:

Probability of an event happening = Number of ways it can happen Total number of outcomes

Example: the chances of rolling a "4" with a die

Number of ways it can happen: 1 (there is only 1 face with a "4" on it)

Total number of outcomes: 6 (there are 6 faces altogether)

So the probability = 1 6

Example: there are 5 marbles in a bag: 4 are blue, and 1 is red. What is the probability that a blue marble gets picked?

Number of ways it can happen: 4 (there are 4 blues)

Total number of outcomes: 5 (there are 5 marbles in total)

So the probability = 4 5 = 0.8

Probability Line

We can show probability on a Probability Line :

Probability is always between 0 and 1

Probability is Just a Guide

Probability does not tell us exactly what will happen, it is just a guide

Example: toss a coin 100 times, how many Heads will come up?

Probability says that heads have a ½ chance, so we can expect 50 Heads .

But when we actually try it we might get 48 heads, or 55 heads ... or anything really, but in most cases it will be a number near 50.

Learn more at Probability Index .

Some words have special meaning in Probability:

Experiment : a repeatable procedure with a set of possible results.

Example: Throwing dice

We can throw the dice again and again, so it is repeatable.

The set of possible results from any single throw is {1, 2, 3, 4, 5, 6}

Outcome: A possible result.

Example: "6" is one of the outcomes of a throw of a die.

Trial: A single performance of an experiment.

Example: I conducted a coin toss experiment. After 4 trials I got these results:

Three trials had the outcome "Head", and one trial had the outcome "Tail"

Sample Space: all the possible outcomes of an experiment.

Example: choosing a card from a deck

There are 52 cards in a deck (not including Jokers)

So the Sample Space is all 52 possible cards : {Ace of Hearts, 2 of Hearts, etc... }

The Sample Space is made up of Sample Points:

Sample Point: just one of the possible outcomes

Example: Deck of Cards

• the 5 of Clubs is a sample point
• the King of Hearts is a sample point

"King" is not a sample point. There are 4 Kings, so that is 4 different sample points.

There are 6 different sample points in that sample space.

Event: one or more outcomes of an experiment

Example Events:

An event can be just one outcome:

• Getting a Tail when tossing a coin
• Rolling a "5"

An event can include more than one outcome:

• Choosing a "King" from a deck of cards (any of the 4 Kings)
• Rolling an "even number" (2, 4 or 6)

Hey, let's use those words, so you get used to them:

Example: Alex wants to see how many times a "double" comes up when throwing 2 dice.

The Sample Space is all possible Outcomes (36 Sample Points):

{1,1} {1,2} {1,3} {1,4} ... ... ... {6,3} {6,4} {6,5} {6,6}

The Event Alex is looking for is a "double", where both dice have the same number. It is made up of these 6 Sample Points :

{1,1} {2,2} {3,3} {4,4} {5,5} and {6,6}

These are Alex's Results:

 After 100 Trials , Alex has 19 "double" Events ... is that close to what you would expect?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.3: Probability Rules- “And” and “Or”

• Last updated
• Save as PDF
• Page ID 91507

• Maxie Inigo, Jennifer Jameson, Kathryn Kozak, Maya Lanzetta, & Kim Sonier
• Coconino Community College

Learning Objectives

Students will be able to:

• Determine if two events are mutually exclusive and/or independent.
• Apply the "Or" rule to calculate the probability that either of two events occurs.
• Apply the "And" rule to calculate the probability that both of two events occurs.

Many probabilities in real life involve more than one event. If we draw a single card from a deck we might want to know the probability that it is either red or a jack. If we look at a group of students, we might want to know the probability that a single student has brown hair and blue eyes. When we combine two events we make a single event called a compound event . To create a compound event, we can use the word “and” or the word “or” to combine events. It is very important in probability to pay attention to the words “and” and “or” if they appear in a problem. The word “and” restricts the field of possible outcomes to only those outcomes that simultaneously describe all events. The word “or” broadens the field of possible outcomes to those that describe one or more events.

Example \(\PageIndex{1}\): Counting Students

Suppose a teacher wants to know the probability that a single student in her class of 30 students is taking either Art or English. She asks the class to raise their hands if they are taking Art and counts 13 hands. Then she asks the class to raise their hands if they are taking English and counts 21 hands. The teacher then calculates

\[P(\text{Art or English}) = \dfrac{13+21}{30} = \dfrac{33}{30} \nonumber\]

The teacher knows that this is wrong because probabilities must be between zero and one, inclusive. After thinking about it she remembers that nine students are taking both Art and English. These students raised their hands each time she counted, so the teacher counted them twice. When we calculate probabilities we have to be careful to count each outcome only once.

Mutually Exclusive Events

An experiment consists of drawing one card from a well shuffled deck of 52 cards. Consider the events E : the card is red, F : the card is a five, and G : the card is a spade. It is possible for a card to be both red and a five at the same time but it is not possible for a card to be both red and a spade at the same time. It would be easy to accidentally count a red five twice by mistake. It is not possible to count a red spade twice.

Definition: Mutually Exclusive

Two events are mutually exclusive if they have no outcomes in common.

Example \(\PageIndex{2}\): Mutually Exclusive with Dice

Two fair dice are tossed and different events are recorded. Let the events E , F and G be as follows:

• E = {the sum is five} = {(1, 4), (2, 3), (3, 2), (4, 1)}
• F = {both numbers are even} = {(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)}
• G = {both numbers are less than five} = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4,1), (4, 2), (4, 3), (4,4)}
• Are events E and F mutually exclusive?

Yes. E and F are mutually exclusive because they have no outcomes in common. It is not possible to add two even numbers to get a sum of five.

• Are events E and G mutually exclusive?

No. E and G are not mutually exclusive because they have some outcomes in common. The pairs (1, 4), (2, 3), (3, 2) and (4, 1) all have sums of 5 and both numbers are less than five.

• Are events F and G mutually exclusive?

No. F and G are not mutually exclusive because they have some outcomes in common. The pairs (2, 2), (2, 4), (4, 2) and (4, 4) all have two even numbers that are less than five.

Addition Rule for “Or” Probabilities

The addition rule for probabilities is used when the events are connected by the word “or”. Remember our teacher in Example \(\PageIndex{1}\) at the beginning of the section? She wanted to know the probability that her students were taking either art or English. Her problem was that she counted some students twice. She needed to add the number of students taking art to the number of students taking English and then subtract the number of students she counted twice. After dividing the result by the total number of students she will find the desired probability. The calculation is as follows:

\[ \begin{align*} P(\text{art or English}) &= \dfrac{\# \text{ taking art + } \# \text{ taking English - } \# \text{ taking both}}{\text{total number of students}} \\[4pt] &= \dfrac{13+21-9}{30} \\[4pt] &= \dfrac{25}{30} \approx {0.833} \end{align*}\]

The probability that a student is taking art or English is 0.833 or 83.3%.

When we calculate the probability for compound events connected by the word “or” we need to be careful not to count the same thing twice. If we want the probability of drawing a red card or a five we cannot count the red fives twice. If we want the probability a person is blonde-haired or blue-eyed we cannot count the blue-eyed blondes twice. The addition rule for probabilities adds the number of blonde-haired people to the number of blue-eyed people then subtracts the number of people we counted twice.

If A and B are any events then

\[P(A\, \text{or}\, B) = P(A) + P(B) – P(A \,\text{and}\, B).\]

If A and B are mutually exclusive events then \(P(A \,\text{and}\, B) = 0\), so then

\[P(A \, \text{or}\, B) = P(A) + P(B).\]

Example \(\PageIndex{3}\): Additional Rule for Drawing Cards

A single card is drawn from a well shuffled deck of 52 cards. Find the probability that the card is a club or a face card.

There are 13 cards that are clubs, 12 face cards (J, Q, K in each suit) and 3 face cards that are clubs.

\[ \begin{align*} P(\text{club or face card}) &= P(\text{club}) + P(\text{face card}) - P(\text{club and face card}) \\[4pt] &= \dfrac{13}{52} + \dfrac{12}{52} - \dfrac{3}{52} \\[4pt] &= \dfrac{22}{52} = \dfrac{11}{26} \approx {0.423} \end{align*}\]

The probability that the card is a club or a face card is approximately 0.423 or 42.3%.

A simple way to check this answer is to take the 52 card deck and count the number of physical cards that are either clubs or face cards. If you were to set aside all of the clubs and face cards in the deck, you would end up with the following:

{2 Clubs, 3 Clubs, 4 Clubs, 5 Clubs, 6 Clubs, 7 Clubs, 8 Clubs, 9 Clubs, 10 Clubs, J Clubs, Q Clubs, K Clubs, A Clubs, J Hearts, Q Hearts, K Hearts, J Spades, Q Spades, K Spades, J Diamonds, Q Diamonds, K Diamonds}

That is 22 cards out of the 52 card deck, which gives us a probably of: \[ \begin{align*} \dfrac{22}{52} = \dfrac{11}{26} \approx {0.423} \end{align*}\]

This confirms our earlier answer using the formal Addition Rule.

Example \(\PageIndex{4}\): Addition Rule for Tossing a Coin and Rolling a Die

An experiment consists of tossing a coin then rolling a die. Find the probability that the coin lands heads up or the number is five.

Let H represent heads up and T represent tails up. The sample space for this experiment is S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}.

• There are six ways the coin can land heads up, {H1, H2, H3, H4, H5, H6}.
• There are two ways the die can land on five, {H5, T5}.
• There is one way for the coin to land heads up and the die to land on five, {H5}.

\[ \begin{align*} P(\text{heads or five}) &= P(\text{heads}) + P(\text{five}) - P(\text{both heads and five}) \\[4pt] &= \dfrac{6}{12} + \dfrac{2}{12} - \dfrac{1}{12} \\[4pt] &= \dfrac{7}{12} = \approx {0.583} \end{align*}\]

The probability that the coin lands heads up or the number is five is approximately 0.583 or 58.3%.

Example \(\PageIndex{5}\): Addition Rule for Satisfaction of Car Buyers

Two hundred fifty people who recently purchased a car were questioned and the results are summarized in the following table.

Find the probability that a person bought a new car or was not satisfied.

\[\begin{align*} P(\text{new car or not satisfied}) &= P(\text{new car}) + P(\text{not satisfied}) - P(\text{new car and not satisfied}) \\[4pt] &= \dfrac{120}{250} + \dfrac{75}{250} - \dfrac{28}{250} = \dfrac{167}{250} \approx 0.668 \end{align*}\]

The probability that a person bought a new car or was not satisfied is approximately 0.668 or 66.8%.

Independent Events

Sometimes we need to calculate probabilities for compound events that are connected by the word “and.” Tossing a coin multiple times or rolling dice are independent events. Each time you toss a fair coin the probability of getting heads is ½. It does not matter what happened the last time you tossed the coin. It’s similar for dice. If you rolled double sixes last time that does not change the probability that you will roll double sixes this time. Drawing two cards without replacement is not an independent event. When you draw the first card and set it aside, the probability for the second card is now out of 51 cards not 52 cards.

Definition: Independent Events

Two events are independent events if the occurrence of one event has no effect on the probability of the occurrence of the other event.

Example \(\PageIndex{6}\): Determining When Events are Independent

Are these events independent?

a) A fair coin is tossed two times. The two events are (1) first toss is a head and (2) second toss is a head.

b) The two events (1) “It will rain tomorrow in Houston” and (2) “It will rain tomorrow in Galveston” (a city near Houston).

c) You draw a card from a deck, then draw a second card without replacing the first.

a) The probability that a head comes up on the second toss is \(\frac{1}{2}\) regardless of whether or not a head came up on the first toss, so these events are independent .

b) These events are not independent because it is more likely that it will rain in Galveston on days it rains in Houston than on days it does not.

c) The probability of the second card being red depends on whether the first card is red or not, so these events are not independent .

Multiplication Rule for “And” Probabilities: Independent Events

If events A and B are independent events, then \( P(\text{A and B}) = P(A) \cdot P(B)\).

Example \(\PageIndex{7}\): Independent Events for Tossing Coins

Suppose a fair coin is tossed four times. What is the probability that all four tosses land heads up?

The tosses of the coins are independent events. Knowing a head was tossed on the first trial does not change the probability of tossing a head on the second trial.

\(P(\text{four heads in a row}) = P(\text{1st heads and 2nd heads and 3rd heads and 4th heads})\)

\( = P(\text{1st heads}) \cdot P(\text{2nd heads}) \cdot P(\text{3rd heads}) \cdot P(\text{4th heads})\)

\( = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2}\)

\( = \dfrac{1}{16}\)

The probability that all four tosses land heads up is \(\dfrac{1}{16}\).

Example \(\PageIndex{8}\): Independent Events for Drawing Marbles

A bag contains five red and four white marbles. A marble is drawn from the bag, its color recorded and the marble is returned to the bag. A second marble is then drawn. What is the probability that the first marble is red and the second marble is white?

Since the first marble is put back in the bag before the second marble is drawn these are independent events.

\[\begin{align*} P(\text{1st red and 2nd white}) &= P(\text{1st red}) \cdot P(\text{2nd white}) \\[4pt] &= \dfrac{5}{9} \cdot \dfrac{4}{9} = \dfrac{20}{81}\end{align*}\]

The probability that the first marble is red and the second marble is white is \(\dfrac{20}{81}\).

Example \(\PageIndex{9}\): Independent Events for Faulty Alarm Clocks

Abby has an important meeting in the morning. She sets three battery-powered alarm clocks just to be safe. If each alarm clock has a 0.03 probability of malfunctioning, what is the probability that all three alarm clocks fail at the same time?

Since the clocks are battery powered we can assume that one failing will have no effect on the operation of the other two clocks. The functioning of the clocks is independent.

\[\begin{align*} P(\text{all three fail}) &= P(\text{first fails}) \cdot P(\text{second fails})\cdot P(\text{third fails}) \\[4pt] &= (0.03)(0.03)(0.03) \\[4pt] &= 2.7 \times 10^{-5} \end{align*}\]

The probability that all three clocks will fail is approximately 0.000027 or 0.0027%. It is very unlikely that all three alarm clocks will fail.

At Least Once Rule for Independent Events

Many times we need to calculate the probability that an event will happen at least once in many trials. The calculation can get quite complicated if there are more than a couple of trials. Using the complement to calculate the probability can simplify the problem considerably. The following example will help you understand the formula.

Example \(\PageIndex{10}\): At Least Once Rule

The probability that a child forgets her homework on a given day is 0.15. What is the probability that she will forget her homework at least once in the next five days?

Assume that whether she forgets or not one day has no effect on whether she forgets or not the second day.

If P (forgets) = 0.15, then P (not forgets) = 0.85.

\[\begin{align*} P(\text{forgets at least once in 5 tries}) &= P(\text{forgets 1, 2, 3, 4 or 5 times in 5 tries}) \\[4pt] & = 1 - P(\text{forgets 0 times in 5 tries}) \\[4pt] &= 1 - P(\text{not forget}) \cdot P(\text{not forget}) \cdot P(\text{not forget}) \cdot P(\text{not forget}) \cdot P(\text{not forget}) \\[4pt] &= 1 - (0.85)(0.85)(0.85)(0.85)(0.85) \\[4pt] & = 1 - (0.85)^{5} = 0.556 \end{align*}\]

The probability that the child will forget her homework at least one day in the next five days is 0.556 or 55.6%

The idea in Example \(\PageIndex{9}\) can be generalized to get the At Least Once Rule.

Definition: At Least Once Rule

If an experiment is repeated n times, the n trials are independent and the probability of event A occurring one time is P(A) then the probability that A occurs at least one time is: \(P(\text{A occurs at least once in n trials}) = 1 - P(\overline{A})^{n}\)

Example \(\PageIndex{11}\): At Least Once Rule for Bird Watching

The probability of seeing a falcon near the lake during a day of bird watching is 0.21. What is the probability that a birdwatcher will see a falcon at least once in eight trips to the lake?

Let A be the event that he sees a falcon so P(A) = 0.21. Then, \(P(\overline{A}) = 1 - 0.21 = 0.79\).

\(P(\text{at least once in eight tries}) = 1 - P(\overline{A})^{8}\)

\( = 1 - (0.79)^{8}\)

\( = 1 - (0.152) = 0.848\)

The probability of seeing a falcon at least once in eight trips to the lake is approximately 0.848 or 84.8%.

Example \(\PageIndex{12}\): At Least Once Rule for Guessing on Multiple Choice Tests

A multiple choice test consists of six questions. Each question has four choices for answers, only one of which is correct. A student guesses on all six questions. What is the probability that he gets at least one answer correct?

Let A be the event that the answer to a question is correct. Since each question has four choices and only one correct choice, \(P(\text{correct}) = \dfrac{1}{4}\).

That means \(P(\text{not correct}) =1 - \dfrac{1}{4} = \dfrac{3}{4}\).

\[ \begin{align*} P(\text{at least one correct in six trials}) &= 1 - P(\text{not correct})^{6} \\[4pt] &= 1 - \left(\dfrac{3}{4}\right)^{6} \\[4pt] &= 1 - (0.178) = 0.822 \end{align*}\]

The probability that he gets at least one answer correct is 0.822 or 82.2%.

Probabilities from Two-Way Tables

Two-way tables can be used to define events and find their probabilities using two different approaches: intuitively or using the probability rules. We can calculate “and” and "or" probabilities by combining the data in relevant cells.

Example \(\PageIndex{13}\): Probabilities from a Two-Way Table

Continuation of Example \(\PageIndex{5}\):

A person is chosen at random. Find the probability that the person:

• bought a new car

\[\begin{align*} P(\text{new car}) &= \dfrac{\text{number of new car}}{\text{number of people}} \\[4pt] &= \dfrac{120}{250} = 0.480 = 48.0 \% \end{align*} \]

• was satisfied

\[\begin{align*} P(\text{satisfied}) &= \dfrac{\text{number of satisfied}}{\text{number of people}} \\[4pt] &= \dfrac{175}{250} = 0.700 = 70.0 \% \end{align*} \]

• bought a new car and was satisfied

\[\begin{align*} P(\text{new car and satisfied}) &= \dfrac{\text{number of new car and satisfied}}{\text{number of people}} \\[4pt] &= \dfrac{92}{250} = 0.368 = 36.8 \% \end{align*} \]

• bought a new car or was satisfied

\[\begin{align*} P(\text{new car or satisfied}) &= \dfrac{\text{number of new car + number of satisfied - number of new car and satisfied}}{\text{number of people}} \\[4pt] &= \dfrac{120 + 175 - 92}{250} = \dfrac{203}{250} = 0.812 = 81.2 \% \end{align*} \]

Engaging Probability Games and Activities

By: Author Sarah Carter

Posted on Published: September 25, 2022  - Last updated: March 18, 2024

Categories Probability

This blog post contains Amazon affiliate links. As an Amazon Associate, I earn a small commission from qualifying purchases.

Want to check out my favorite Amazon items for the classroom? Check out my Amazon favorites page !  

Looking for some fun ways to teach probability? Check out this collection of 9 engaging probability games and activities that are perfect for any unit on data analysis and probability.

Probability Games for the Middle School or High School Classroom

When I first started teaching, the only way I knew to review probability with my students was to give them multiple-choice questions like they would likely see on the state test at the end of the year. These questions usually revolved around weather events or selling school raffle tickets. My students were not enthused. 

I decided to switch things up and have my students experience experimental probability and theoretical probability for themselves by having them participate in various probability games. These games are suitable for the middle school or high school classroom. I have even received emails from college math professors using these games with their students. 

Every student will enjoy embracing the excitement of chance and challenge as they explore the important concepts of theoretical and experimental probability. My goal is to share games that are easy to play, simple to explain, and use supplies that teachers already have in their classroom such as  linking cubes , a deck of cards, or  dice .

This  Blocko Probability game  is a fun way to introduce the difference between experimental and theoretical probability to students.

I play the game with  linking cubes  with my students, but you could actually use any collection of small items.

Probability Bingo

Probability Bingo is not your typical bingo game! It is designed to help students build an understanding of probability by thinking through all of the possible combinations of colors that can be rolled. 

Students fill their bingo boards based on the color combinations they think will appear the most. The winner is the person who fills out their entire bingo board first.

Greedy Pig Dice Game

I have been playing this greedy pig dice game with my students to practice probability since I learned it while student teaching!

All you need for this game is a set of dice !

Teaching Probability with Deal or No Deal

Students will enjoy calculating probabilities while playing through a  game of Deal or No Deal ! So many different probability concepts can be discussed while you work through a simulation of the popular tv game show.

There are many other game shows that you could pull ideas from for other probability-based lessons. 

Left Center Right Game

There is so much probability to explore with the Left Center Right Dice game . I love playing a few rounds of Left Center Right to kick off my probability units!

Probability Exploration Activities

When it comes to teaching probability, hands-on activities are the secret ingredient to making math lessons memorable and impactful. In this section, we’ll delve into a variety of engaging probability activities that you can seamlessly integrate into your middle or high school math curriculum.

These probability activities use easy-to-find supplies such as linking cubes , hex nuts, rope, and cardstock .

Mystery Box Probability Activity

Can your students use their knowledge of probability to determine the contents of the  mystery box  using the relative frequency of the colors? 

Hex Nut Probability Activity

All you need for this fun and engaging hex nut probability activity are hex nuts, empty soda bottles, and a plastic ring.

Probability with Cuboctahedrons

Your students will enjoy building cuboctahedrons and using them to explore a fun probability question!

Marriage Probability Activity

My high school students really enjoyed exploring the probability behind an old fable regarding the likelihood of getting married in the next year.

More Resources for Teaching Probability

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 6: Probability

About this unit, venn diagrams and the addition rule.

• Probability with Venn diagrams (Opens a modal)
• Addition rule for probability (Opens a modal)
• Addition rule for probability (basic) (Opens a modal)
• Two-way tables, Venn diagrams, and probability Get 3 of 4 questions to level up!

Multiplication rule for probabilities

• Compound probability of independent events (Opens a modal)
• Independent events example: test taking (Opens a modal)
• General multiplication rule example: independent events (Opens a modal)
• Dependent probability introduction (Opens a modal)
• General multiplication rule example: dependent events (Opens a modal)
• Interpreting general multiplication rule (Opens a modal)
• Probability with general multiplication rule Get 3 of 4 questions to level up!
• Interpret probabilities of compound events Get 3 of 4 questions to level up!

Conditional probability

• Conditional probability and independence (Opens a modal)
• Conditional probability with Bayes' Theorem (Opens a modal)
• Conditional probability using two-way tables (Opens a modal)
• Conditional probability tree diagram example (Opens a modal)
• Tree diagrams and conditional probability (Opens a modal)
• Calculate conditional probability Get 3 of 4 questions to level up!

Probability from simulations

• Experimental versus theoretical probability simulation (Opens a modal)
• Random number list to run experiment (Opens a modal)
• Random numbers for experimental probability (Opens a modal)
• Simulation and randomness: Random digit tables (Opens a modal)
• Statistical significance of experiment (Opens a modal)
• Interpret results of simulations Get 3 of 4 questions to level up!

Permutations

• Factorial and counting seat arrangements (Opens a modal)
• Permutation formula (Opens a modal)
• Possible three letter words (Opens a modal)
• Zero factorial or 0! (Opens a modal)
• Ways to arrange colors (Opens a modal)
• Ways to pick officers (Opens a modal)
• Permutations Get 3 of 4 questions to level up!

Combinations

• Intro to combinations (Opens a modal)
• Combination formula (Opens a modal)
• Handshaking combinations (Opens a modal)
• Combination example: 9 card hands (Opens a modal)
• Combinations Get 3 of 4 questions to level up!

Probability using combinatorics

• Probability using combinations (Opens a modal)
• Example: Lottery probability (Opens a modal)
• Example: Different ways to pick officers (Opens a modal)
• Probability with permutations & combinations example: taste testing (Opens a modal)
• Probability with combinations example: choosing groups (Opens a modal)
• Probability with combinations example: choosing cards (Opens a modal)
• Mega millions jackpot probability (Opens a modal)
• Probability with permutations and combinations Get 3 of 4 questions to level up!

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

2.4 - how to assign probability to events.

We know that probability is a number between 0 and 1. How does an event get assigned a particular probability value? Well, there are three ways of doing so:

• the personal opinion approach
• the relative frequency approach
• the classical approach

On this page, we'll take a look at each approach.

The Personal Opinion Approach Section  

This approach is the simplest in practice, but therefore it also the least reliable. You might think of it as the "whatever it is to you" approach. Here are some examples:

• "I think there is an 80% chance of rain today."
• "I think there is a 50% chance that the world's oil reserves will be depleted by the year 2100."
• "I think there is a 1% chance that the men's basketball team will end up in the Final Four sometime this decade."

Example 2-4 Section  

At which end of the probability scale would you put the probability that:

• one day you will die?
• you can swim around the world in 30 hours?
• you will win the lottery someday?
• a randomly selected student will get an A in this course?
• you will get an A in this course?

The Relative Frequency Approach Section  

The relative frequency approach involves taking the follow three steps in order to determine P ( A ), the probability of an event A :

• Perform an experiment a large number of times, n , say.
• Count the number of times the event A of interest occurs, call the number N ( A ), say.
• Then, the probability of event A equals:

\(P(A)=\dfrac{N(A)}{n}\)

The relative frequency approach is useful when the classical approach that is described next can't be used.

Example 2-5 Section  

When you toss a fair coin with one side designated as a "head" and the other side designated as a "tail", what is the probability of getting a head?

I think you all might instinctively reply \(\dfrac{1}{2}\). Of course, right? Well, there are three people who once felt compelled to determine the probability of getting a head using the relative frequency approach:

As you can see, the relative frequency approach yields a pretty good approximation to the 0.50 probability that we would all expect of a fair coin. Perhaps this example also illustrates the large number of times an experiment has to be conducted in order to get reliable results when using the relative frequency approach.

By the way, Count Buffon (1707-1788) was a French naturalist and mathematician who often pondered interesting probability problems. His most famous question

Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two strips?

came to be known as Buffon's needle problem. Karl Pearson (1857-1936) effectively established the field of mathematical statistics. And, once you hear John Kerrich's story, you might understand why he, of all people, carried out such a mind-numbing experiment. He was an English mathematician who was lecturing at the University of Copenhagen when World War II broke out. He was arrested by the Germans and spent the war interned in a prison camp in Denmark. To help pass the time he performed a number of probability experiments, such as this coin-tossing one.

Example 2-6 Section  

Some trees in a forest were showing signs of disease. A random sample of 200 trees of various sizes was examined yielding the following results:

What is the probability that one tree selected at random is large?

There are 68 large trees out of 200 total trees, so the relative frequency approach would tell us that the probability that a tree selected at random is large is 68/200 = 0.34.

What is the probability that one tree selected at random is diseased?

There are 37 diseased trees out of 200 total trees, so the relative frequency approach would tell us that the probability that a tree selected at random is diseased is 37/200 = 0.185.

What is the probability that one tree selected at random is both small and diseased?

There are 8 small, diseased trees out of 200 total trees, so the relative frequency approach would tell us that the probability that a tree selected at random is small and diseased is 8/200 = 0.04.

What is the probability that one tree selected at random is either small or disease-free?

There are 121 trees (35 + 46 + 24 + 8 + 8) out of 200 total trees that are either small or disease-free, so the relative frequency approach would tell us that the probability that a tree selected at random is either small or disease-free is 121/200 = 0.605.

What is the probability that one tree selected at random from the population of medium trees is doubtful of disease?

There are 92 medium trees in the sample. Of those 92 medium trees, 32 have been identified as being doubtful of disease. Therefore, the relative frequency approach would tell us that the probability that a medium tree selected at random is doubtful of disease is 32/92 = 0.348.

The Classical Approach Section  

The classical approach is the method that we will investigate quite extensively in the next lesson. As long as the outcomes in the sample space are equally likely (!!!), the probability of event \(A\) is:

\(P(A)=\dfrac{N(A)}{N(\mathbf{S})}\)

where \(N(A)\) is the number of elements in the event \(A\), and \(N(\mathbf{S})\) is the number of elements in the sample space \(\mathbf{S}\). Let's take a look at an example.

Example 2-7 Section  

Suppose you draw one card at random from a standard deck of 52 cards. Recall that a standard deck of cards contains 13 face values (Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, and King) in 4 different suits (Clubs, Diamonds, Hearts, and Spades) for a total of 52 cards. Assume the cards were manufactured to ensure that each outcome is equally likely with a probability of 1/52. Let \(A\) be the event that the card drawn is a 2, 3, or 7. Let \(B\) be the event that the card is a 2 of hearts (H), 3 of diamonds (D), 8 of spades (S) or king of clubs (C). That is:

• \(A= \{x: x \text{ is a }2, 3,\text{ or }7\}\)
• \(B = \{x: x\text{ is 2H, 3D, 8S, or KC}\}\)
• What is the probability that a 2, 3, or 7 is drawn?
• What is the probability that the card is a 2 of hearts, 3 of diamonds, 8 of spades or king of clubs?
• What is the probability that the card is either a 2, 3, or 7 or a 2 of hearts, 3 of diamonds, 8 of spades or king of clubs?
• What is \(P(A\cap B)\)?

Browse Course Material

Course info.

• Prof. Scott Sheffield

Departments

• Mathematics

As Taught In

• Discrete Mathematics
• Probability and Statistics

Learning Resource Types

Probability and random variables, assignments.

Assignments include problems from the required textbook.

Ross, Sheldon. A First Course in Probability . 8th ed. Pearson Prentice Hall, 2009. ISBN: 9780136033134.

You are leaving MIT OpenCourseWare

Search This Blog

Cbse mathematics.

Basic concepts, definitions and formulas of mathematics, mathematics assignments for 9th standard to 10+2 standard, maths study material for 8th, 9th, 10th, 11th, 12th classes, Mathematics lesson plan for classes 8th,10th and 12th standard, Interesting maths riddles and maths magic, Class-wise mathematics study material for students from 8th to 12. A complete resource centre of mathematics for students and teachers

Featured Posts

Maths assignment class viii | quadrilateral, math assignment class xi ch -16 | probability,   math assignment  class xi  ch -16 | probability.

Extra questions of chapter 16 probability class 11  with answers and  hints to the difficult questions. strictly according to the cbse syllabus. Important and useful math. assignment for the students of class 11

Given P(A) =3/5 and PB) =1/5 . If A and B are mutually exclusive events, then find   P (A or B)

Ans:   4/5

Probability of not getting 12 as the sum in a throw of two dice is

A card is drawn from a deck of 52 cards. Find the probability of getting a king or a heart or a red card.

Two balls are drawn simultaneously from a bag containing 5 white and 7 red balls, find the probability that both the balls are red.

Define mutually exclusive events.

Ans: A & B are said to be mutually exclusive events if A ⋂ B = ф or There is no common element in A and B.

A coin is tossed and then a dice thrown write the sample space hence find the probability of getting a head and a prime number

Ans: 3/12 or 1/4

The probability of two events A and B are 0.25 and 0.50 respectively. The probability of their simultaneous occurrence (occurrence of both) is 0.14. Find the probability that neither A nor B occurs. 

The probability of happening of an event A is 0.5 and that of B is 0.3. If A and B are mutually exclusive events then find the probability of neither A nor B.

In a job interview for 4 posts, 5 boys and 3 girls appeared. If selection of each candidate is equiprobable then find the probability that

i) 3 boys and 1 girl or 1 boy and 3 girls are selected.         

Ans   1/2

(ii) At most one girl is selected                                                

Find the probability that when a hand of 7 cards is drawn from a well shuffled deck of 52 cards, it contains

(i) all Kings     Ans: 1/7735

(ii) 3 Kings     Ans: 9/1547

(iii) at least 3 Kings. Ans 46/7735

If an integer from 1 through 1000 is chosen at random, then find the probability that the integer is a multiple of 2 or a multiple of 9.

Multiple of 2 from 1 to 1000 are 2, 4, 6, 8, ..., 1000

Let n be the number of terms of above series.

∴ nth term = 1000

2 + (n - 1)2 = 1000

      2 + 2n - 2 = 1000

               2n = 1000

              ∴ n = 500

The number of multiple of 2 are 500.

The multiple of 9 are 9, 18, 27, ..., 999

Let m be the number of term in above series.

∴ m th term = 999

9 + (m - 1)9 = 999

  9 + 9m – 9 = 999

               9m = 999

              ∴ m = 111

The number of multiple of 9 are 111.

The multiple of 2 and 9 both are 18, 36, ..., 990

Let p be the number of terms in above series.

∴ pth term = 990

18 + (p - 1)18 = 990

18 + 18p – 18 = 990

                 18p = 990

                     P = 55

The number of multiple of 2 and 9 are 55.

∴ Number of multiple of 2 or 9 = 500 + 111 − 55 = 556

∴ Required probability = 556/1000 = 0.556

If A and B are mutually exclusive events, P (A) = 0 35. and P (B) = 0.45, then Find

(i) P(A’)                 Ans 0.65

(ii) P(B’)               Ans: 0.55

(iii) P(A ⋃ B)         Ans: 0.80

(iv) P(A ⋂ B)         Ans: 0

(v) P(A ⋂ B’)        Ans 0.35

(vi) P(A’ ⋂ B’)        Ans: 0.2

A bag contains 8 red and 5 white balls. Three balls are drawn at random.  Find the probability that

(i) all the three balls are white.

(ii) all the three balls are red.

Ans: 28/143

(iii) one ball is red and two balls are white.

Ans: 40/143

If a card is drawn from a deck of 52 cards, then find the probability of getting a king or a heart or a red card.

A drawer contains 50 bolts and 150 nuts. Half of the bolt and half of nuts are rusted. If one of then is chosen at random, what is the probability that it is rusted or bolt ?

Ans: 125/200 = 5/8

A box contains 24 balls from 1 to 24. One ball is drawn at random. Find the probability that ball drawn has a number which is a multiple of 3 or 4.

A, B, C are three mutually exclusive and exhaustive events associated with a random experiment

Solution Hint: Use  P(A) + P(B) + P(C) = 1

Two candidates Sunil and Ravi appeared in an interview. The probability that Sunil will qualify the interview is 0.04 and that Ravi will qualify the interview is 0.2. The probability that both will qualify the interview is 0.03. Find the probability that

(i) Both Sunil and Ravi will not qualify the interview.

Answer: 0.79 

Solution Hint: P(A’  ⋂ B’) = P(A  ⋃ B)’ = 1- P(A  ⋃ B)

(ii) Only one of them will qualify the interview.

Answer: 0.18

Solution Hint : P(A ⋂ B’) + P(A’ ⋂ B) = P(A) – P(A ⋂ B) + P(B) – P(A ⋂ B)

A and B are two mutually exclusive and exhaustive events of a random experiment such that P(A) = 6[P(B)] 2 where P(A) and P(B) denotes probabilities of A and B respectively. Find P(A) and P(B).

Ans: P(A) = 2/3,  P(B) = 1/3

Solution Hint:  P(A) + P(B) = 1

6[P(B)] 2  + P(B) = 1

Now putting P(B) = x and then solve the quadratic equation for the value of x  

A box contains 10 bulbs, of which three are defective. If a random sample of 5 bulbs is drawn, find the probabilities that the sample contains

(i) Exactly two defective bulbs

(ii) At the most one defectiv e bulb.

In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that

(i) The student opted for NCC or NSS.

(ii) The student has opted neither NCC nor NSS.

(iii) The student has opted NSS but not NCC.

Out of 100 students, two sections of 40 and 60 are formed. If you and your friend are among the 100 students, what is the probability that

(a) you both enter the same section?  

(b) you both enter the different sections?  

If 4-digit numbers greater than 5,000 are randomly formed from the digits 0, 1, 3, 5, and 7, what is the probability of forming a number divisible by 5 when,

(i) the digits are repeated? 

Ans : 99/249

(ii) the repetition of digits is not allowed?  

The probability that a student will pass the final examination in both English and Hindi is 0.5 and probability of passing neither is 0.1.  If the probability of passing the English examination is 0.75.  What is the probability of passing the Hindi examination? 

Solution Hint:

P(E ⋂H) = 0.5

P(E'⋂H') = 0.1 ⇒ P(E⋃H)' = 0.1

⇒1- P(E⋃H) = 0.1

⇒P(E⋃H) = 0.9

Now using P(E⋃H) = P(E) + P(H) - P(E⋂H) we get

P(H) = 0.65

An urn contains 7 white balls, 5 black balls and 3 red balls. Two balls are drawn at random. Find the probability that: 

(a) both the balls are red

(b) One ball is red and other is black

If the letters of the word ‘ALGORITHM’ are arranged at random in a row what is the probability the letters ‘GOR’ must remain together as a unit?

Number of letters in the word ‘ALGORITHM’ = 9

If ‘GOR’ remain together, then considered it as 1 group.

∴  Number of letters = 6+1 =    7

Number of word, if ‘GOR’ remain together = 7!

Total number of words from the letters of the word ‘ALGORITHM’ = 9!

∴  Required probability =    7! / 9! = 1/72

Two students A and B appeared in an examination. The probability that A will qualify the examination is 0.05 and that B will qualify the examination is 0.10. The probability that both will qualify the examination is 0.02.

Based on the above information answer the following questions

a) What is the probability that both A and B will not qualify the examination ?

Solution Hint

P(both will not qualify the examination) = P(A' ⋂B') 

P(A⋃B)' = 1- P(A⋃B) = 0.87

b) What is the probability that at least one of them will not qualify the examination?

P(At least one of them will not qualify) = 1- P(both will qualify)

= 1-  P(A ⋂B) = 1-0.02 = 0.98

c) What is the probability that only one of them will qualify the examination?

P(Only one will qualify) = P(A - B) + P(B - A)

= P(A ⋂B') + P(B⋂A')

= P(A) - P (A ⋂B) + P(B) - P (A ⋂B) 

= 0.05 - 0.02 + 0.1 - 0.02 = 0.11

A card is drawn from a deck of 52 cards. The probability of getting a King or a Heart or a Red card is

Answer: 7/13

Sarah is participating in a game where 5-digit numbers are formed and one number is chosen at random. She wants to strategize to increase her chances of winning.

Using the information provided, help Sarah answer the following questions

(i) What is the probability of choosing an odd number ?

(ii) What is the probability of choosing a number divisible by 5?

(iii) What is the probability of choosing a number whose value is less than 20000 ?

(iv) What is the probability of choosing a number whose unit digit is either 7 or 9?

Download PDF form of this Assignment

THANKS FOR YOUR VISIT

PLEASE COMMENT BELOW

Post a Comment

Breaking news, popular post on this blog, lesson plan maths class 10 | for mathematics teacher.

Lesson Plan Math Class 10 (Ch-1) | Real Numbers

Lesson Plan Maths Class XII | For Maths Teacher

• Assignment 10 15
• Assignment 11 12
• Assignment 12 14
• Assignment 8 8
• Assignment 9 5
• Lesson plan 10 15
• Lesson Plan 12 13
• Lesson Plan 8 10
• Maths 10 20
• Maths 11 21
• Maths 12 17

SUBSCRIBE FOR NEW POSTS

Get new posts by email:.